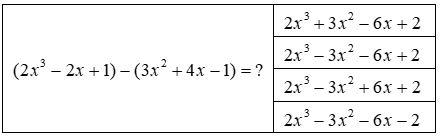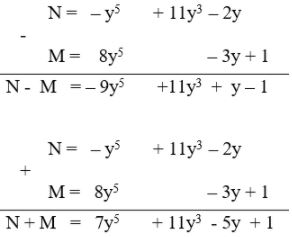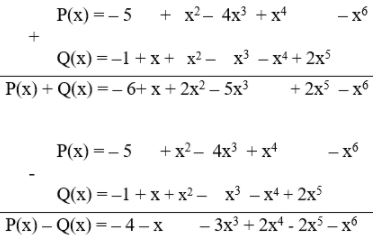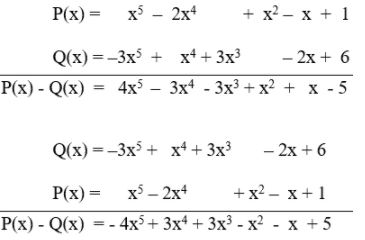Giải bài tập SGK Toán 7 Bài 8: Cộng, trừ đa thức một biến
Hướng dẫn Giải bài tập SGK Toán 7 Bài Cộng, trừ đa thức một biến sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung
1. Giải bài 44 trang 45 SGK Toán 7
2. Giải bài 45 trang 45 SGK Toán 7
3. Giải bài 46 trang 45 SGK Toán 7
4. Giải bài 47 trang 45 SGK Toán 7
5. Giải bài 48 trang 46 SGK Toán 7
6. Giải bài 49 trang 46 SGK Toán 7
7. Giải bài 50 trang 46 SGK Toán 7
8. Giải bài 51 trang 46 SGK Toán 7

1. Giải bài 44 trang 45 SGK Toán 7
Cho hai đa thức: \(P(x) = - 5{x^3} - \dfrac{1}{3} + 8{x^4} + {x^2}\)
và \(Q(x) = {x^2} - 5x - 2{x^3} + {x^4} - \dfrac{2}{3}\).
Hãy tính \(P(x) + Q(x)\) và \(P(x) - Q(x)\).
Phương pháp giải
Sắp xếp hai đa thức theo lũy thừa giảm dần của biến rồi sau đó thực hiện phép tính cộng hoặc phép tính trừ theo hàng dọc.
Hướng dẫn giải
Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:
\(P(x) = 8{x^4} - 5{x^3} + {x^2} - \dfrac{1}{3}\) ;
\(Q(x) = {x^4} - 2{x^3} + {x^2} - 5x - \dfrac{2}{3}\).
Thực hiện phép tính ta có:
2. Giải bài 45 trang 45 SGK Toán 7
Cho đa thức \(P(x) = {x^4} - 3{x^2} + \dfrac{1}{2} - x\).
Tìm các đa thức \(Q(x), R(x)\), sao cho:
a) \(P(x) + Q(x) = {x^5} - 2{x^2} + 1\)
b) \(P(x) – R(x) = {x^3}\)
Phương pháp giải
Câu a:
\(Q(x)\) là số hạng chưa biết. Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
Câu b:
\(R(x)\) là số trừ. Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
Hướng dẫn giải
Câu a:
Ta có: \(P(x) = {x^4} - 3{x^2} + \dfrac{1}{2} - x\)
Vì \(P(x) + Q(x) = {x^5} - 2{x^2} + 1\) nên
Vậy \(Q(x)=x^5-x^4+x^2+x+\dfrac{1}{2}\)
Câu b:
Ta có: \(P(x) = {x^4} - 3{x^2} + \dfrac{1}{2} - x\)
Vì \(P(x) – R(x) = {x^3}\) nên \(R\left( x \right) = P\left( x \right) - {x^3}\)
Do đó:
\(\eqalign{
& R(x) = {x^4} - 3{x^2} + {1 \over 2} - x - {x^3} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\, = {x^4} - {x^3} - 3{x^2} - x + {1 \over 2} \cr} \)
3. Giải bài 46 trang 45 SGK Toán 7
Viết đa thức \(P\left( x \right) = 5{x^3}-4{x^2} + 7x - 2\) dưới dạng:
a) Tổng của hai đa thức một biến.
b) Hiệu của hai đa thức một biến.
Bạn Vinh nêu nhận xét: "Ta có thể viết đa thức đã cho thành tổng của hai đa thức bậc \(4\)". Đúng hay sai ? Vì sao ?
Phương pháp giải
Câu a:
Để cộng, trừ hai đa thức một biến, ta có thể thực hiện theo một trong hai cách sau:
Cách 1. Thực hiện theo cách cộng, trừ đa thức đã học ở Bài 6.
Cách 2. Sắp xếp các hạng tử của hai đa thức cùng theo lũy thừa giảm (hoặc tăng) của biến, rồi đặt phép tính theo cột dọc tương tự như cộng, trừ các số (chú ý đặt các đơn thức đồng dạng ở cùng một cột).
Câu b:
Để cộng, trừ hai đa thức một biến, ta có thể thực hiện theo một trong hai cách sau:
Cách 1. Thực hiện theo cách cộng, trừ đa thức đã học ở Bài 6.
Cách 2. Sắp xếp các hạng tử của hai đa thức cùng theo lũy thừa giảm (hoặc tăng) của biến, rồi đặt phép tính theo cột dọc tương tự như cộng, trừ các số (chú ý đặt các đơn thức đồng dạng ở cùng một cột).
Hướng dẫn giải
Câu a:
Có nhiều cách viết, ví dụ:
Cách 1: Nhóm các hạng tử của đa thức \(P(x)\) thành 2 đa thức khác nhau.
Chẳng hạn: \(P(x) = 5{x^3}-4{x^2} + 7x - 2 \)\(\,= (5{x^3}-4{x^2}) + \left( {7x - 2} \right)\)
Vậy \(P(x)\) là tổng của hai đa thức một biến là: \(5x^3 – 4x^2\) và \(7x – 2\)
Cách 2: Viết các hạng tử của đa thức \(P(x)\) thành tổng hay hiệu của hai đơn thức. Sau đó nhóm thành 2 đa thức khác nhau.
Chẳng hạn: Viết \(5x^3 = 4x^3 + x^3;\)
\( – 4x^2 = – 6x^2 + 2x^2\)
Nên: \(P(x) = 5x^3 – 4x^2 +7x – 2 \)
\(= 4x^3 + x^3 – 6x^2 + 2x^2 +7x – 2\)
\(P(x) = (4x^3 – 6x^2 + 7x) \)\(+ (x^3 + 2x^2 – 2)\)
Vậy \(P(x)\) là tổng của hai đa thức một biến là: \(4x^3 – 6x^2 + 7x\) và \(x^3 + 2x^2 – 2.\)
Câu b:
Hiệu của hai đa thức một biến.
\(P(x)=5{x^3}-4{x^2} + 7x - 2\)
\(\, = (5{x^3} + 7x) - (4{x^2} + 2)\)
Hay \(P(x)\) là hiệu của hai đa thức một biến là: \(5x^3 + 7x \) và \(4x^2 + 2\)
Cách khác: \(P(x) = 5x^3 – 4x^2 +7x – 2 \)
\(= (5x^3 – 4x^2) – (-7x + 2)\)
Hay \(P(x)\) là hiệu của hai đa thức một biến là: \(5x^3 – 4x^2\) và \(-7x + 2\)
Chú ý: Đáp số ở câu a; b không duy nhất, các bạn có thể tìm thêm đa thức khác.
Bạn Vinh nói đúng: Ta có thể viết đa thức đã cho thành tổng của hai đa thức bậc \(4\) chẳng hạn như:
\(P(x)=5{x^3}-4{x^2} + 7x - 2 \)\(\,= (2{x^4} + 5{x^3} + 7x) \)\(\,+(-2{x^4}-4{x^2} - 2)\).
Vậy \(P(x)\) là tổng của hai đa thức bậc 4 là: \(2x^4 + 5x^3 + 7x\) và \(–2x^4 – 4x^2 – 2\)
(Phần này có vô số cách viết, miễn sao tổng hai hệ số của \(x^4\) là bằng \(0\))
4. Giải bài 47 trang 45 SGK Toán 7
Cho các đa thức:
\(P\left( x \right) = 2{x^4}-x-2{x^3} + 1\)
\(Q\left( x \right) = 5{x^2}-{x^3} + 4x\)
\(H\left( x \right) = -2{x^4} + {x^2} + 5\).
Tính \(P(x) + Q(x) + H(x)\) và \(P(x) - Q(x) - H(x)\).
Phương pháp giải
Ta có thể sắp xếp các đa thức theo lũy thừa giảm dần, sau đó xếp các số hạng đồng dạng theo cùng cột dọc rồi thực hiện phép tính.
Hướng dẫn giải
Sắp xếp các đa thức theo lũy thừa giảm dần ta có
\(P\left( x \right) = 2{x^4}-x-2{x^3} + 1 \)
\(\,= 2{x^4}-2{x^3}-x + 1\)
\(Q\left( x \right) = 5{x^2} - {x^3} + 4x \)
\(\,= - {x^3} + 5{x^2} + 4x\)
\(H\left( x \right) = -2{x^4} + {x^2} + 5\)
Xếp các số hạng đồng dạng theo cùng cột dọc rồi thực hiện tính ta có:
5. Giải bài 48 trang 46 SGK Toán 7
Chọn đa thức mà em cho là kết quả đúng:
Phương pháp giải
Thực hiện phép tính trừ hai đa thức để tìm kết quả sau đó so sánh với các đáp án để chọn đáp án đúng.
- Bước 1: Bỏ dấu ngoặc theo quy tắc dấu ngoặc
- Bước 2: Nhóm các hạng tử đồng dạng với nhau
- Bước 3: Thực hiện cộng trừ các đơn thức đồng dạng.
Hướng dẫn giải
\(\eqalign{
& (2{x^3} - 2x + 1) - (3{x^2} + 4x - 1) \cr
& = 2{x^3} - 2x + 1 - 3{x^2} - 4x + 1 \cr
& = 2{x^3} - 3{x^2} + \left( { - 2x - 4x} \right) + \left( {1 + 1} \right) \cr
& = 2{x^3} - 3{x^2} - 6x + 2 \cr} \)
Vậy chọn đa thức thứ hai.
6. Giải bài 49 trang 46 SGK Toán 7
Hãy tìm bậc của mỗi đa thức sau:
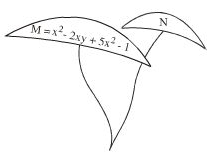
\(M = {x^2} - 2xy + 5{x^2} - 1\)
\(N = {x^2}{y^2} - {y^2} + 5{x^2} - 3{x^2}y + 5\).
Phương pháp giải
- Thu gọn các đa thức nếu được.
- Xác định bậc của đa thức: Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Hướng dẫn giải
- Đa thức \(M = {x^2} - 2xy + 5{x^2} - 1\)
\(\eqalign{
& M = {x^2} - 2xy + 5{x^2} - 1 \cr
& \,\,\,\,\,\,\,\,\, = \left( {{x^2} + 5{x^2}} \right) - 2xy - 1 \cr
& \,\,\,\,\,\,\,\,\, = 6{x^2} - 2xy - 1 \cr} \)
Hạng tử \(6{x^2}\) có bậc \(2\); hạng tử \(-2xy\) có bậc \(2\) ;hạng tử \(-1\) có bậc \(0\).
Bậc cao nhất trong các bậc đó là \(2\).
Vậy đa thức \(M\) có bậc \(2\).
- Đa thức \(N = {x^2}{y^2} - {y^2} + 5{x^2} - 3{x^2}y + 5\)
Hạng tử \({x^2}{y^2}\) có bậc \(2+2=4\); hạng tử \( - {y^2}\) có bậc \(2\); hạng tử \(5{x^2}\) có bậc \(2\); hạng tử \( - 3{x^2}y\) có bậc là \(2+1=3\); hạng tử \(5\) có bậc \(0\).
Bậc cao nhất trong các bậc đó là \(4\).
Vậy đa thức \(N\) có bậc \(4\).
7. Giải bài 50 trang 46 SGK Toán 7
Cho các đa thức:
\(N = 15{y^3} + 5{y^2} - {y^5} - 5{y^2} - 4{y^3} \)\(\,- 2y\)
\(M = {y^2} + {y^3} - 3y + 1 - {y^2} + {y^5} -{y^3} \)\(\,+ 7{y^5}\).
a) Thu gọn các đa thức trên.
b) Tính \(N + M\) và \(N - M\).
Phương pháp giải
Câu a:
- Thu gọn các đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng.
Câu b:
- Để cộng (hay trừ) hai đa thức, ta làm các bước sau:
- Bước 1: Viết hai đa thức trong dấu ngoặc
- Bước 2: Thực hiện bỏ dấu ngoặc (theo quy tắc dấu ngoặc)
- Bước 3: Nhóm các hạng tử đồng dạng
- Bước 4: Cộng, trừ các đơn thức đồng dạng.
Hướng dẫn giải
Thu gọn các đa thức:
Câu a:
\(N = 15y^3 + 5y^2 – y^5 – 5y^2 – 4y^3 – 2y\)
\(= –y^5 + (15y^3 – 4y^3) + (5y^2 – 5y^2) – 2y\)
\(= –y^5 + 11y^3 + 0 – 2y\)
\(= – y^5 + 11y^3 – 2y.\)
Và \(M = y^2 + y^3 – 3y + 1 – y^2 + y^5 – y^3 + 7y^5\)
\(= (y^5 + 7y^5) + (y^3 – y^3) + (y^2 – y^2) – 3y + 1\)
\(= 8y^5 + 0 + 0 – 3y + 1.\)
\(= 8y^5 – 3y + 1.\)
Câu b:
8. Giải bài 51 trang 46 SGK Toán 7
Cho hai đa thức:
\(P\left( x \right) = 3{x^2} - 5 + {x^4} - 3{x^3} - {x^6} - 2{x^2} \)\(\,- {x^3}\);
\(Q\left( x \right) = {x^3} + 2{x^5} - {x^4} + {x^2} - 2{x^3}\)\(\, + x - 1\)
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
b) Tính \(P(x) + Q(x)\) và \(P(x) - Q(x)\).
Phương pháp giải
Câu a:
- Thu gọn các đa thức đã cho rồi sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Câu b:
- Để cộng hoặc trừ hai đa thức, ta có thể đặt phép tính theo cột dọc tương tự như cộng, trừ các số (chú ý đặt các đơn thức đồng dạng ở cùng một cột).
Hướng dẫn giải
Câu a:
\(P(x) = 3x^2 – 5 + x^4 – 3x^3 – x^6 – 2x^2 – x^3\)
\(= – x^6 + x^4 + (– 3x^3 – x^3) + (3x^2 – 2x^2) – 5\)
\(= – x^6 + x^4 – 4x^3 + x^2 – 5.\)
\(= – 5+ x^2 – 4x^3 + x^4 – x^6\)
Và \(Q(x) = x^3 + 2x^5 – x^4 + x^2 – 2x^3 + x –1\)
\(= 2x^5 – x^4 + (x^3 – 2x^3) + x^2 + x –1\)
\(= 2x^5 – x^4 – x^3 + x^2 + x –1.\)
\(= –1+ x + x^2 – x^3 – x^4 + 2x^5\)
Câu b:
Vậy: \(P(x) + Q(x) = – 6 + x + 2x^2 – 5x^3 + 2x^5 – x^6\)
\(P(x) – Q(x) = – 4 – x – 3x^3 + 2x^4 - 2x^5 – x^6 \)
9. Giải bài 52 trang 46 SGK Toán 7
Tính giá trị của đa thức \(P\left( x \right) = {x^2} - 2x - 8\) tại: \(x = -1; x = 0\) và \(x = 4\).
Phương pháp giải
Thay giá trị của \(x\) vào đa thức \(P(x)\) rồi tính giá trị của biểu thức đó.
Hướng dẫn giải
Ta có \(P\left( x \right) = {x^2} - 2x - 8\)
Thay \(x=-1\) vào \(P(x)\) ta được:
\(P\left( { - 1} \right) = {\left( { - 1} \right)^2} - 2.\left( { - 1} \right) - 8 \)
\(\,= 1 + 2 - 8 = - 5\)
Thay \(x=0\) vào \(P(x)\) ta được:
\(P\left( 0 \right) = {0^2} - 2.0 - 8 = - 8\)
Thay \(x=4\) vào \(P(x)\) ta được:
\(P\left( 4 \right) = {4^2} - 2.4 - 8 = 16 - 8 - 8 = 0\).
10. Giải bài 53 trang 46 SGK Toán 7
Cho các đa thức:
\(P\left( x \right) = {x^5} - 2{x^4} + {x^2} - x + 1\)
\(Q\left( x \right) = 6 - 2x + 3{x^3} + {x^4} - 3{x^5}\)
Tính \(P(x) - Q(x)\) và \(Q(x) - P(x)\). Có nhận xét gì về các hệ số của hai đa thức tìm được ?
Phương pháp giải
- Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm của biến.
- Để trừ hai đa thức, ta có thể đặt phép tính theo cột dọc tương tự như trừ các số (chú ý đặt các đơn thức đồng dạng ở cùng một cột).
Hướng dẫn giải
- Sắp xếp các hạng tử của đa thức \(Q(x)\) theo lũy thừa giảm của biến:
\( Q\left( x \right) = 6 - 2x + 3{x^3} + {x^4} - 3{x^5}\)
\(\, = - 3{x^5} + {x^4} + 3{x^3} - 2x + 6 \)
- Thực hiện tính ta có:
Nhận xét: Các hệ số tương ứng của hai đa thức \(P(x)-Q(x)\) và \(Q(x)-P(x)\) đối nhau.
Chú ý: Ta gọi 2 đa thức có các hệ số tương ứng đối nhau là đa thức đối nhau.
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Khái niệm về biểu thức đại số
- doc Giải bài tập SGK Toán 7 Bài 2: Giá trị của một biểu thức đại số
- doc Giải bài tập SGK Toán 7 Bài 3: Đơn thức
- doc Giải bài tập SGK Toán 7 Bài 4: Đơn thức đồng dạng
- doc Giải bài tập SGK Toán 7 Bài 5: Đa thức
- doc Giải bài tập SGK Toán 7 Bài 6: Cộng, trừ đa thức
- doc Giải bài tập SGK Toán 7 Bài 7: Đa thức một biến
- doc Giải bài tập SGK Toán 7 Bài 9: Nghiệm của đa thức một biến
- doc Giải bài tập SGK Toán 7 Ôn tập Chương 4: Biểu thức đại số



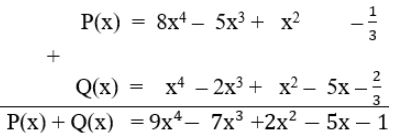
.JPG)
.JPG)