Giải bài tập SGK Toán 7 Bài 3: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh

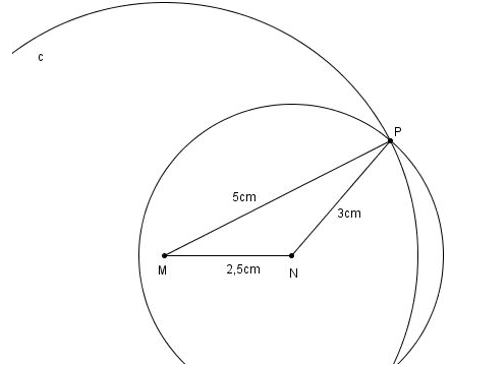
Vẽ tam giác \(MNP\), biết \(MN=2,5 cm, NP=3cm, PM= 5cm\)

Phương pháp giải:

Dựng tam giác \(ABC\) biết \(AB=c;BC=a;AC=b\)

- Vẽ đoạn \(BC= a\)

- Trên cùng một nửa mặt phẳng bờ \(BC\) vẽ cung tròn tâm \(B\) bán kính \(c\) và cung tròn tâm \(C\) bán kính \(b\).

- Hai cung tròn cắt nhau tại \(A\).

- Vẽ các đoạn \(AB,AC\), ta được tam giác \(ABC\).

Hướng dẫn giải:

- Vẽ đoạn \(MN= 2,5cm\)

- Trên cùng một nửa mặt phẳng bờ \(MN\) vẽ cung tròn tâm \(M\) bán kính \(5cm\) và cung tròn tâm \(N\) bán kính \(3cm\).

- Hai cung tròn cắt nhau tại \(P\).

- Vẽ các đoạn \(MP, NP\), ta được tam giác \(MNP\).

Vẽ tam giác biết độ dài mỗi cạnh là \(3\) cm. Sau đó đo góc của tam  giác.

Phương pháp giải:

Dựng tam giác \(ABC\) biết \(AB=c;BC=a;AC=b\)

- Vẽ đoạn \(BC= a\)

- Trên cùng một nửa mặt phẳng bờ \(BC\) vẽ cung tròn tâm \(B\) bán kính \(c\) và cung tròn tâm \(C\) bán kính \(b\).

- Hai cung tròn cắt nhau tại \(A\).

- Vẽ các đoạn \(AB,AC\), ta được tam giác \(ABC\).

Hướng dẫn giải:

- Vẽ đoạn thẳng \(AB=3\,cm\)

- Trên cùng một nửa mặt phẳng bờ \(AB\) vẽ cung tròn tâm \(A\) bán kính \(3\,cm\) và cung tròn tâm \(B\) bán kính \(3\,cm\)

- Hai cung tròn cắt nhau tại \(C\).

- Vẽ các đoạn thẳng \(AC, BC\); ta được tam giác \(ABC\) 

- Đo mỗi góc của tam giác \(ABC\) ta được:

\(\widehat{A}=\widehat{B}=\widehat{C}= 60^0\)

Trên mỗi hình sau có tam giác nào bằng nhau? Vì sao? 

Phương pháp giải:

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì  hai tam giác đó bằng nhau.

Hướng dẫn giải:

Hình 68.

Xét \(∆ABC\) và \(∆ABD\) có:

 +) \(AB\) cạnh chung

 +) \(AC= AD\) (gt)

 +) \(BC=BD\) (gt)

\( \Rightarrow  ∆ABC= ∆ABD\) (c.c.c)

Hình 69. 

Xét \(∆MNQ\) và \(∆QPM \) có: 

+) \(MN = QP\) (gt)

+) \(NQ = PM\) (gt)

+) \(MQ\) cạnh chung

\( \Rightarrow ∆MNQ = ∆QPM \) (c.c.c)

Hình 70.

Xét \(∆EHI\) và \(∆IKE\) có: 

+) \(EH = IK\) (gt)

+) \(HI = KE\) (gt)

+) \(EI\) cạnh chung

\( \Rightarrow  ∆EHI = ∆IKE\) (c.c.c)

Xét \(∆EHK\) và \(∆IKH\) có:

+) \(EH = IK\) (gt)

+) \(EK = IH\) (gt)

+) \(HK\) cạnh chung

\( \Rightarrow ∆EHK = ∆IKH\) (c.c.c)

(Chú ý: gt là giả thiết)  

Xét bài toán: "\(\Delta AMB\) và \(\Delta ANB\) có \(MA=MB, NA=NB\) (h.71). Chứng minh rằng \(\widehat{AMN}=\widehat{BMN}\)."

1) Hãy ghi giả thiết và kết luận của bài toán.

2) Hãy sắp xếp bốn câu sau đây một cách hợp lý để giải bài toán trên :

a) Do đó  \(\Delta AMN=\Delta BMN (c.c.c)\)

b)

\(MN\) cạnh chung

\(MA=MB\) ( giả thiết)

\(NA= NB\) ( giả thiết)

c) Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc tương ứng)

d) \(\Delta AMN\) và \(\Delta BMN\) có: 

Phương pháp giải:

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì  hai tam giác đó bằng nhau.

Hướng dẫn giải:

1) 

2) Sắp xếp theo thứ tự: d, b, a, c. 

d) \(\Delta AMN\) và \(\Delta BMN\) có: 

b)

\(MN\) cạnh chung

\(MA=MB\) ( giả thiết)

\(NA= NB\) ( giả thiết)

a) Do đó  \(\Delta AMN=\Delta BMN (c.c.c)\) 

c) Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc tương ứng)

Cho hình 72. Chứng minh rằng:

a) \(∆ADE = ∆BDE\).

b) \(\widehat{DAE}=\widehat{DBE}\). 

Phương pháp giải:

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Hướng dẫn giải:

Xem hình vẽ: 

Câu a: Xét \(∆ADE\) và \(∆BDE\) có:

+) \(DE\) cạnh chung

+) \(AD=BD\) (giả thiết)

+) \(AE=BE\) (giả thiết)

Vậy \( ∆ADE=∆BDE\) (c.c.c)

Câu b: Từ \(∆ADE=∆BDE\) (chứng minh trên)

Suy ra \(\widehat{DAE}=\widehat{DBE}\) (hai góc tương ứng). 

Cho góc \(xOy\) (h.73), Vẽ cung tròn tâm \(O\), cung tròn này cắt \(Ox, Oy\)  theo thứ tự ở \(A,B\) (1). Vẽ các cung tròn tâm \(A\) và tâm \(B\) có cùng bán kính sao cho chúng cắt nhau ở điểm \(C\) nằm trong góc \(xOy\) ((2) (3)). Nối \(O\) với \(C\) (4). Chứng minh \(OC\) là tia phân giác của góc \(xOy\).

Phương pháp giải:

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì  hai tam giác đó bằng nhau.

Hướng dẫn giải:

Vì \(A,B\) cùng thuộc cung tròn tâm \(O\) nên \(OA=OB\) (cùng bằng bán kính của cung tròn)

Vì \(C\) thuộc cung tròn tâm \(A\) và thuộc cung tròn tâm \(B\) mà 2 cung tròn này cùng bán kính nên \(AC=BC\) 

Nối \(BC, AC\).

Xét \(∆OBC\) và \(∆OAC\) có:

+) \(OB=OA\) (chứng minh trên)

+) \(BC=AC\) (chứng minh trên)

+) \(OC\)  cạnh chung

\( \Rightarrow ∆OBC = ∆OAC(c.c.c)\)

\( \Rightarrow \widehat{BOC}=\widehat{AOC}\) (hai góc tương ứng)

Vậy \(OC\) là tia phân giác của góc \(xOy\).

Cho tam giác \(ABC\). Dùng thước và compa, vẽ các tia phân giác của các góc \(A,B,C.\)

Phương pháp giải:

Áp dụng kết quả của bài 20 trang 115 SGK Toán 7 Tập 1.

Hướng dẫn giải:

Cách vẽ phân giác của góc A (Dựa trên kết quả bài 20).

Vẽ cung tròn tâm A cung này cắt tia AB ,AC theo thứ tự ở M,N

Vẽ các cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau ở điểm I.

Nối AI, ta được AI là tia phân giác của góc A.

- Tương tự cho cách vẽ tia phân giác của góc B, C

Cho góc \(xOy\) và tia \(Am\) (h.74a)

Vẽ cung trong tâm \(O\) bán kính \(r\), cung tròn này cắt \(Ox,Oy\) theo thứ tự ở \(B,C\)

Vẽ cung tròn tâm \(A\) bán kính \(r\), cung này cắt kia \(Am\) ở \(D\) (h.74b).

Vẽ cung tròn tâm \(D\) có bán kính bằng \(BC\), cung tròn này cắt cung tròn tâm \(A\) bán kính \(r\) ở \(E\) (h. 74c). 

Chứng minh rằng: \(\widehat{DAE}=\widehat{xOy}.\) 

Phương pháp giải:

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì  hai tam giác đó bằng nhau.

Hướng dẫn giải:

Kí hiệu \((O;r)\) là đường tròn tâm \(O\) bán kính \(r\). 

Vì \(B, C\) thuộc \((O; r)\) nên \(OB = OC = r.\)

\(D\) thuộc \((A;r)\) nên \(AD = r.\)

\(E\) thuộc \((D; BC)\) và \((A;r)\) nên \(AE = r, DE = BC.\)

Xét \(\Delta DAE\) và \(\Delta BOC\) có: 

\(AD=OB(=r)\)

\(DE=BC\) (chứng minh trên)

\(AE=OC(=r)\)

Suy ra \(∆ DAE= ∆ BOC\;(c.c.c)\)

Suy ra  \(\widehat{DAE}=\widehat{BOC}\) (hai góc tương ứng)

Mà \(\widehat{BOC}=\widehat{xOy}.\)

 Do đó: \(\widehat{DAE}=\widehat{xOy}\) (điều phải chứng minh).

Cho đoạn thẳng \(AB\) dài \(4cm\) Vẽ đường tròn tâm \(A\) bán kính \(2cm\) và đường tròn tâm \(B\) bán kính \(3cm\), chúng cắt nhau ở \(C\) và \(D\), chứng minh rằng \(AB\) là tia phân giác của góc \(CAD\)

Phương pháp giải:

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Hướng dẫn giải:

Vì \(C\) là giao của đường tròn tâm \(A\) và đường tròn tâm \(B\) nên \(AC=2cm,BC=3cm\) 

Vì \(D\) là giao của đường tròn tâm \(A\) và đường tròn tâm \(B\) nên \(AD=2cm,BD=3cm\)

Do đó \(AC=AD,BC=BD\) 

Xét \(∆BAC\) và \(∆ BAD\) có:

\(AC=AD\) (chứng minh trên)

\(BC=BD\) (chứng minh trên)

\(AB\) cạnh chung.

Suy ra \(∆ BAC= ∆ BAD(c.c.c)\)

Suy ra \(\widehat{BAC}\) = \(\widehat{BAD}\) (hai góc tương ứng)

Vậy \(AB\) là tia phân giác của góc \(CAD\).