Giải bài tập SGK Toán 11 Nâng cao Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Có bao nhiêu khả năng có thể xảy ra đối với thứ tự giữa các đội trong một giải bóng đá có 5 đội bóng? (Giả sử rằng không có hai đội nào có điểm trùng nhau).

Phương pháp giải:

Sử dụng hoán vị 5 phần tử.

Hướng dẫn giải:

Mỗi cách xếp thứ tự cho 5 đội bóng là một hoán vị của 5 phần tử.

Vậy có 5! = 120 khả năng.

Giả sử có 8 vận động viên tham gia chạy thi. Nếu không kể trường hợp có hai vận động viên về đích cùng một lúc thì có bao nhiêu kết quả có thể xảy ra đối với các vị trí thứ nhất, thứ nhì và thứ ba ?

Phương pháp giải:

Việc xếp thứ tự nhất nhì ba thực chất là chọn ra 3 trong 8 VĐV và xếp thứ tự cho họ.

Do đó mỗi cách chọn và xếp thứ tự này chính là một chỉnh hợp chập 3 của 8.

Hướng dẫn giải:

Ba vị trí nhất nhì ba là một chỉnh hợp chập 3 của 8 phần tử nên

Có \(A_8^3 = 8.7.6 = 336\) kết quả.

Trong mặt phẳng cho một tập hợp P gồm n điểm. Hỏi:

a) Có bao nhiêu đoạn thẳng mà hai đầu mút thuộc P?

b) Có bao nhiêu vectơ khác vectơ \(\overrightarrow 0 \) mà điểm đầu và điểm cuối thuộc P ?

Phương pháp giải:

a) Số đoạn thẳng mà hai đầu mút là hai điểm thuộc P chính bằng số tổ hợp chập 2 của n phần tử.

b) Số vectơ cần tìm bằng số chỉnh hợp chập 2 của n phần tử.

Hướng dẫn giải:

a) Mỗi cách chọn ra 2 điểm trong tập hợp P có n điểm và nối chúng lại ta được một đoạn thẳng. (không phân biệt thứ tự)

Vậy số đoạn thẳng mà hai đầu mút là hai điểm thuộc P chính bằng số tổ hợp chập 2 của n phần tử, tức là \(C_n^2 = {{n\left( {n - 1} \right)} \over 2}.\)

b) Mỗi cách chọn ra 2 phân tử trong tập hợp P gồm n phần tử và sắp xếp thứ tự cho chúng sẽ được một véctơ.

Do đó số vectơ cần tìm bằng số chỉnh hợp chập 2 của n phần tử, tức là bằng \( A_n^2 = n\left( {n - 1} \right).\)

Trong một Ban chấp hành đoàn gồm 7 người, cần chọn 3 người vào ban thường vụ.

a) Nếu không có sự phân biệt về chức vụ của 3 người trong ban thường vụ thì có bao nhiêu cách chọn?

b) Nếu cần chọn 3 người vào ban thường vụ với các chức vụ: Bí thư, Phó Bí thư, Ủy viên thường vụ thì có bao nhiêu cách chọn?

Phương pháp giải:

a) Số cách chọn 3 người mà không có sự phân biệt về chức vụ trong ban thường vụ bằng số tổ hợp chập 3 của 7 phân tử.

b) Số cách chọn 3 người với các chức vụ : Bí thư, Phó bí thư, Ủy viên thường vụ bằng số chỉnh hợp chập 3 của 7 phần tử.

Hướng dẫn giải:

a) Số cách chọn 3 người mà không có sự phân biệt về chức vụ trong ban thường vụ bằng số tổ hợp chập 3 của 7 phân tử.

Do đó có \(C_7^3 = 35\) cách chọn.

b) Số cách chọn 3 người với các chức vụ : Bí thư, Phó bí thư, Ủy viên thường vụ bằng số chỉnh hợp chập 3 của 7 phần tử.

Do đó có \(A_7^3 = 210\) cách chọn.

Một bài thi trắc nghiệm khách quan gồm 10 câu. Mỗi câu có 4 phương án trả lời. Hỏi bài thi đó có bao nhiêu phương án trả lời?

Phương pháp giải:

Mỗi phương án trả lời cho cả bài thi là một công việc được thực hiện qua 10 bước mới hết nên cần đếm mỗi bước có bao nhiêu cách chọn rồi dùng quy tắc nhân.

Hướng dẫn giải:

Câu 1 có 4 cách chọn đáp án.

Câu 2 có 4 cách chọn đáp án.

...

Câu 10 có 4 cách chọn đáp án.

Theo quy tắc nhân, bài thi có \(4^{10}= 1048576\) phương án trả lời.

Có bao nhiêu số tự nhiên có 6 chữ số và chia hết cho 5?

Phương pháp giải:

Số chia hết cho 5 thì có chữ số tận cùng bằng 0 hoặc 5.

Đếm số cách chọn của mỗi chữ số và dùng quy tắc nhân.

Hướng dẫn giải:

Một số có 6 chữ số và chia hết cho 5 có dạng \(\overline {abcdeg } \)

+) a khác 0 nên có 9 cách chọn.

+) \(g\in\) {0; 5} nên có hai cách chọn.

+) b, c, d, e mỗi chữ số có 10 cách chọn.

Vậy theo quy tắc nhân ta có: \(9.10^4.2 = 180000\) số.

Xét mạng đường nối các tỉnh A, B, C, D, E, F, G, trong đó số viết trên một cạch cho biết số con đường nối hai tỉnh nằm ở haiđầu mút của cạnh (h. 2.2). Hỏi có bao nhiêu cách đi từ tỉnh A đến tỉnh G?

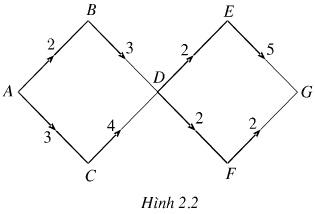
Phương pháp giải:

Liệt kê các trường hợp có thể đi từ A đến G.

Dùng quy tắc nhân đếm số cách đi trong từng TH.

Dùng quy tắc cộng suy ra số cách đi cần tìm.

Hướng dẫn giải:

Có 4 phương án đi qua các tỉnh A đến G là:

a. A → B → D → E → G

b. A → B → D → F → G

c. A → C → D → E → G

d. A → C → D → F → G

Theo quy tắc nhân, ta có:

Phương án a: A → B → D → E → G

Có 2.3.2.5 = 60 cách đi;

Phương án b: A → B → D → F → G

Có 2.3.2.2 = 24 cách đi;

Phương án c: A → C → D → E → G

Có 3.4.2.5 = 120 cách đi;

Phương án d: A → C → D → F → G

Có 3.4.2.2 = 48 cách đi.

Theo quy tắc cộng, ta có: 60 + 24 + 120 + 48 = 252 cách đi từ A đến G.

Xét hồ sơ mạng điện ở hình 2.3 có 6 công tắc khác nhau, trong đó mỗi công tắc có 2 trạng thái đóng và mở.

Hỏi có bao nhiêu cách đóng – mở 6 công tắc để mạng điện thông mạch từ P đến Q (tức là có dòng điện từ P đến Q)?

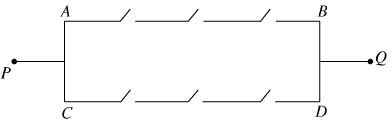
Phương pháp giải:

Liệt kê các trường hợp có thể thông mạch từ P đến Q

Dùng quy tắc nhân đếm số cách đi trong từng TH.

Dùng quy tắc cộng suy ra số cách đi cần tìm.

Hướng dẫn giải:

TH1: A → B thông mạch, C → D không thông mạch.

Có 1 cách để A → B thông mạch.

Có 7 cách để C → D không thông mạch.

Theo quy tắc nhân có 1.7 = 7 cách.

TH2: A → B không thông mạch, C → D thông mạch.

Có 7 cách để A → B không thông mạch.

Có 1 cách để C → D thông mạch.

Theo quy tắc nhân có 1.7 = 7 cách.

TH3: Cả A → B và C → D thông mạch

Có 1.1 = 1 cách.

Vậy theo quy tắc cộng có 7 + 7 + 1 = 15 cách thông mạch mạng điện.

Một cuộc thi có 15 người tham dự, giả thiết rằng không có hai người nào có điểm bằng nhau.

a) Nếu kết quả của cuộc thi là việc chọn ra 4 người điểm cao nhất thì có bao nhiêu kết quả có thể?

b) Nếu kết qủa của cuộc thi là việc chọn ra các giải nhất, nhì, ba thì có bao nhiêu kết quả có thể?

Phương pháp giải:

a) Số cách chọn ra 4 người điểm cao nhất trong 15 người tham dự là số tổ hợp chập 4 của 15 phần tử. 

b) Số cách chọn ra 3 giải nhất, nhì, ba là số chỉnh hợp chập 3 của 15 phần tử. 

Hướng dẫn giải:

a) Số cách chọn ra 4 người điểm cao nhất trong 15 người tham dự là số tổ hợp chập 4 của 15 phần tử.

Vậy kết quả cần tìm là: \(C_{15}^4 = 1365\)

b) Số cách chọn ra 3 giải nhất, nhì, ba là số chỉnh hợp chập 3 của 15 phần tử.

Vậy kết quả cần tìm là \(A_{15}^3 = 2730\)

Trong một dạ hội cuối năm ở một cơ quan, ban tổ chức phát ra 100 vé xổ số đánh số từ 1 đến 100 cho 100 người. Xổ số có bốn giải : 1 giải nhất, 1 giải nhì, 1 giải ba, 1 giải tư. Kết quả là việc công bố ai trúng giải nhất, giải nhì, giải ba, giải tư. Hỏi :

a) Có bao nhiêu kết quả có thể?

b) Có bao nhiêu kết quả có thể, nếu biết rằng người giữ vé số 47 được giải nhất?

c) Có bao nhiêu kết quả có thể, nếu biết rằng người giữ vé số 47 trúng một trong bốn giải?

Phương pháp giải:

a) Mỗi cách chọn ra 4 người trong 100 người và xếp giải cho mỗi người này là một chính hợp chập 4 của 100 phần tử.

b) c)

- Tìm số kết quả của giải nhất, nhì, ba , tư. 

- Sau đó sử dụng quy tắc nhân.

Hướng dẫn giải:

a) Mỗi cách chọn ra 4 người trong 100 người và xếp giải cho mỗi người này là một chính hợp chập 4 của 100 phần tử.

Vậy có \(A_{100}^4 = 94109400\) kết quả có thể.

b) Người giữ vé số 47 được giải nhất nên chỉ có 1 cách xếp giải nhất.

Nếu giải nhất đã xác định thì ba giải nhì, ba, tư sẽ rơi vào 99 người còn lại.

Mỗi cách chọn 3 người trong 99 người và xếp giải cho họ là 1 chỉnh hợp chập 3 của 99.

Có \(A_{99}^3 = 941094\) cách xếp 3 giải nhì, ba, tư.

Theo quy tắc nhân có 1.941094 = 941094 kết quả có thể.

c) Người giữ vé số 47 có 4 khả năng trúng 1 trong 4 giải.

Sau khi xác định giải của người này thì 3 giải còn lại sẽ rơi vào 99 người không giữ vé số 47.

Vậy có \(A_{99}^3\) khả năng.

Theo quy tắc nhân, có \(4.A_{99}^3 = 3764376\) kết quả có thể.

Một tổ có 8 em nam và 2 em nữ. Người ta cần chọn ra 5 em trong tổ tham dự cuộc thi học sinh thanh lịch của trường. Yêu cầu trong các em được chọn, phải có ít nhất một em nữ. Hỏi có bao nhiêu cách chọn?

Phương pháp giải:

- Xét hai trường hợp sau:

+ TH1: Có 1 nữ, 4 nam.

+ TH2: Có 2 nữ, 3 nam.

- Ở mỗi trường hợp sử dụng tổ hợp và quy tắc nhân để tính.

- Sử dung quy tắc cộng để tính đáp số.

Hướng dẫn giải:

+ TH1: Có 1 nữ, 4 nam

Chọn 1 nữ có 2 cách.

Chọn 4 trong 8 nam có \(C_8^4 = 70\) cách chọn.

Theo quy tắc nhân có 2.70 = 140 cách chọn.

+ TH2: Có 2 nữ, 3 nam.

Chọn 2 nữ có 1 cách.

Chọn 3 trong 8 nam có \(C_8^3 = 56\) cách chọn.

Theo quy tắc nhân có 1.56 = 56 cách chọn.

Vậy theo quy tắc cộng có: 140 + 56 = 196 cách chọn.

Một nhóm học sinh có 7 em nam và 3 em nữ. Người ta cần chọn ra 5 em trong nhóm tham gia đồng diễn thể dục. Trong 5 em được chọn, yêu cầu không có quá một em nữ. Hỏi có bao nhiêu cách chọn?

Phương pháp giải:

- Xét hai trường hợp sau:

+ TH1: Chọn 5 em mà không có em nữ nào.

+ TH2: Chọn 5 em mà chỉ có 1 em nữ.

- Ở mỗi trường hợp sử dụng tổ hợp và quy tắc nhân để tính.

- Sử dung quy tắc cộng để tính đáp số.

Hướng dẫn giải:

+ TH1: Chọn 5 em mà không có em nữ nào.

Số cách chọn 5 em toàn nam là \(C_7^5.\)

+ TH2: Chọn 5 em mà chỉ có 1 em nữ.

Số cách chọn 4 nam và 1 nữ là \(C_7^4.C_3^1\)

Vậy đáp số bài toán là: \(C_7^5 + C_7^4.C_3^1 = 126.\)