Giải bài tập SGK Toán 11 Nâng cao Bài 1: Các hàm số lượng giác
Để các em có thêm nhiều tài liệu tham khảo hữu ích eLib xin giới thiệu đến các em học sinh nội dung giải bài tập SGK Toán 11 Nâng cao bài Các hàm số lượng giác dưới đây. Tài liệu được eLib biên soạn và tổng hợp với nội dung các bài tập có phương pháp và hướng dẫn giải đầy đủ chi tiết, rõ ràng. Mời các em cùng tham khảo.
Mục lục nội dung
1. Giải bài 1 trang 14 SGK Đại số & Giải tích 11 Nâng cao
2. Giải bài 2 trang 14 SGK Đại số & Giải tích 11 Nâng cao
3. Giải bài 3 trang 14 SGK Đại số & Giải tích 11 Nâng cao
4. Giải bài 4 trang 14 SGK Đại số & Giải tích 11 Nâng cao
5. Giải bài 5 trang 14 SGK Đại số & Giải tích 11 Nâng cao
6. Giải bài 6 trang 15 SGK Đại số & Giải tích 11 Nâng cao
7. Giải bài 7 trang 16 SGK Đại số & Giải tích 11 Nâng cao
8. Giải bài 8 trang 16 SGK Đại số & Giải tích 11 Nâng cao
9. Giải bài 9 trang 17 SGK Đại số & Giải tích 11 Nâng cao
10. Giải bài 10 trang 17 SGK Đại số & Giải tích 11 Nâng cao
11. Giải bài 11 trang 17 SGK Đại số & Giải tích 11 Nâng cao

1. Giải bài 1 trang 14 SGK Đại số & Giải tích 11 Nâng cao
Tìm tập xác định của mỗi hàm số sau:
a) \(y = \sqrt {3 - \sin x} \)
b) \( y = {{1 - \cos x} \over {\sin x}}\)
c) \(y = \sqrt {{{1 - \sin x} \over {1 + \cos x}}}\)
d) \(y = \tan \left( {2x + {\pi \over 3}} \right)\)
Phương pháp giải:
a) - Biểu thức \(\sqrt P \) có nghĩa khi \(P\ge 0.\)
- Sử dụng đánh giá \(-1 ≤ \sin x ≤ 1.\)
b) Biểu thức \(\dfrac{P}{Q}\) có nghĩa khi \(Q\ne 0\).
c) Biểu thức \(\sqrt {\frac{P}{Q}} \) xác định khi
\( \left\{ \begin{array}{l} \frac{P}{Q} \ge 0\\ Q \ne 0 \end{array} \right.\)
d) Hàm số y = tan u xác định khi và chỉ khi \(u \ne \frac{\pi }{2} + k\pi\)
Hướng dẫn giải:
a) \(y = \sqrt {3 - \sin x} \)
Vì \(-1 ≤ \sin x ≤ 1\) nên:
\( \begin{array}{l} \Rightarrow 1 \ge - \sin x \ge - 1\\ \Rightarrow 1 + 3 \ge - \sin x + 3 \ge - 1 + 3\\ \Rightarrow 4 \ge 3 - \sin x \ge 2 > 0\\ \Rightarrow 3 - \sin x > 0,\forall x \in R \end{array}\)
Vậy tập xác định của hàm số là: D =\mathbb R
b) \(y = {{1 - \cos x} \over {\sin x}}\) xác định khi và chỉ khi \(\sin x ≠ 0\)
\( ⇔ x ≠ kπ, k \in\mathbb Z\)
Vậy tập xác định \(D =\mathbb R \backslash \left\{ kπ, k \in \mathbb Z\right\}\)
c) \(y = \sqrt {{{1 - \sin x} \over {1 + \cos x}}}\)
ĐK: \(\left\{ \begin{array}{l}\frac{{1 - \sin x}}{{1 + \cos x}} \ge 0\\1 + \cos x \ne 0\end{array} \right.\left( * \right)\)
Ta có:
\(1 \le \sin x \le 1 \Rightarrow 1 - \sin x \ge 0\) với mọi x.
\(1 \le \cos x \le 1 \Rightarrow 1 + \cos x \ge 0\) với mọi x.
\( \Rightarrow \frac{{1 + \sin x}}{{1 + \cos x}} \ge 0\) với mọi x.
Do đó \(\left( * \right) \Leftrightarrow 1 + \cos x \ne 0\)
\( \Leftrightarrow \cos x \ne - 1 \Leftrightarrow x \ne \pi + k2\pi\)
Vậy tập xác định \(D =\mathbb R\backslash\left\{ π + k2π, k \in\mathbb Z\right\}\)
d) \( y = \tan \left( {2x + {\pi \over 3}} \right)\)
Điều kiện xác định: \( \cos \left( {2x + {\pi \over 3}} \right) \ne 0\)
\( \Leftrightarrow 2x + {\pi \over 3} \ne {\pi \over 2} + k\pi \\ \Leftrightarrow 2x \ne \frac{\pi }{6} + k\pi \\ \Leftrightarrow x\ne {\pi \over {12}} + k{\pi \over 2},k \in \mathbb Z\)
Vậy tập xác định \(D =\mathbb R\backslash \left\{ {{\pi \over {12}} + k{\pi \over 2},k \in\mathbb Z} \right\}\)
2. Giải bài 2 trang 14 SGK Đại số & Giải tích 11 Nâng cao
Xét tính chẵn – lẻ của hàm số sau:
a) y = -2sin x
b) y = 3sin x – 2
c) y= sin x – cos x
d) \(y = \sin x\cos^2 x+ \tan x\)
Phương pháp giải:
a) d) Cho hàm số y = f(x)
- Tìm TXĐ D
- Nếu \(x \in D \Rightarrow - x \in D\) và \(f\left( { - x} \right) = - f\left( x \right)\) thì hàm số là hàm số lẻ.
- Nếu \(x \in D \Rightarrow - x \in D\) và \(f\left( { - x} \right) = f\left( x \right)\) thì hàm số là hàm số chẵn.
b) Lấy ví dụ kiểm tra, thay \(x = \frac{\pi }{2}, - x = - \frac{\pi }{2}\) , kiểm tra giá trị của hàm số tại các điểm này và so sánh.
c) Lấy ví dụ kiểm tra, thay \(x = \frac{\pi }{4}, - x = - \frac{\pi }{4}\) , kiểm tra giá trị của hàm số tại các điểm này và so sánh.
Hướng dẫn giải:
a) \(y = f(x) = -2\sin x\)
Tập xác định D = R, ta có:
\( f(-x) = -2\sin (-x) = - 2\left( { - \sin x} \right) = 2\sin x = -f(x), ∀x \in\mathbb R\)
Vậy y = -2sin x là hàm số lẻ.
b) y = f(x) = 3sin x – 2
Ta có: \(f\left( {{\pi \over 2}} \right) = 3\sin \frac{\pi }{2} - 2= 1\)
\( f\left( { - {\pi \over 2}} \right) = 3\sin (-\frac{\pi }{2}) - 2= - 5\)
\( f\left( { - {\pi \over 2}} \right) \ne - f\left( { - {\pi \over 2}} \right)\) và \(f\left( { - {\pi \over 2}} \right) \ne f\left( {{\pi \over 2}} \right)\)
Nên hàm số y = 3sin x – 2 không phải là hàm số chẵn cũng không phải là hàm số lẻ.
c) y = f(x) = sin x – cos x
Ta có: \(f\left( {{\pi \over 4}} \right) = 0;f\left( { - {\pi \over 4}} \right) = - \sqrt 2\)
\( f\left( { - {\pi \over 4}} \right) \ne - f\left( {{\pi \over 4}} \right)\) và \(f\left( { - {\pi \over 4}} \right) \ne f\left( {{\pi \over 4}} \right)\)
Nên y = sin x – cos x không phải là hàm số lẻ cũng không phải là hàm số chẵn.
d) \(y= f\left( x \right) = \sin x{\cos ^2}x + \tan x\)
Tập xác định \(D = \mathbb R \backslash \left\{{\pi \over 2} + k\pi,k \in \mathbb Z \right\}\)
\( ∀x \in D \) ta có \( – x \in D\)
\( \eqalign{ & f\left( { - x} \right) \cr&= \sin \left( { - x} \right){\cos ^2}\left( { - x} \right) + \tan \left( { - x} \right) \cr & = - \sin x{\cos ^2}x - \tan x\cr& = - \left( {\sin x{{\cos }^2}x + \tan x} \right) = - f\left( x \right) \cr}\)
Do đó hàm số đã cho là hàm số lẻ.
3. Giải bài 3 trang 14 SGK Đại số & Giải tích 11 Nâng cao
Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:
a) \( y = 2\cos \left( {x + {\pi \over 3}} \right) + 3\)
b) \( y = \sqrt {1 - \sin \left( {{x^2}} \right)} - 1\)
c) \( y = 4\sin \sqrt x\)
Phương pháp giải:
a) Sử dụng lí thuyết \(- 1 \le \cos u \le 1\) với u là biểu thức của x.
b) c) Sử dụng lí thuyết \(- 1 \le \sin u \le 1\) với u là biểu thức của x.
Hướng dẫn giải:
a) \( y = 2\cos \left( {x + {\pi \over 3}} \right) + 3\)
Ta có: \(-1 ≤ \cos \left( {x + {\pi \over 3}} \right) ≤ 1\)
\( \eqalign{ & \Rightarrow - 2 \le 2\cos \left( {x + {\pi \over 3}} \right) \le 2\cr& \Rightarrow 1 \le 2\cos \left( {x + {\pi \over 3}} \right) + 3 \le 5\cr& \Rightarrow 1 \le y \le 5 \cr &\text{ Vậy }\cr&\min \,y = 1\,khi\,x + {\pi \over 3} = \pi + k2\pi \,\cr&\text{ hay} \,x = {{2\pi } \over 3} + k2\pi \cr &\max \,y = 5\,khi\,x + {\pi \over 3} = k2\pi \cr&\text{ hay} \,x = - {\pi \over 3} + k2\pi \left( {k \in \mathbb Z} \right) \cr} \)
b) \( y = \sqrt {1 - \sin \left( {{x^2}} \right)} - 1\)
ĐK: \(1 - \sin \left( {{x^2}} \right) \ge 0\)
Ta có:
\( - 1 \le \sin {x^2} \le 1\\ \Rightarrow 1 - \left( { - 1} \right) \ge 1 - \sin {x^2} \ge 1 - 1 \\ \Leftrightarrow 2 \ge 1 - \sin {x^2} \ge 0 \Rightarrow 0 \le 1 - \sin {x^2} \le 2 \\ \Rightarrow 0 \le \sqrt {1 - \sin {x^2}} \le \sqrt 2 \\ \Rightarrow 0- 1 \le \sqrt {1 - \sin {x^2}} - 1 \le \sqrt 2 - 1 \\ \Rightarrow - 1 \le y \le \sqrt 2 - 1\)
Vậy min y = - 1 khi \(\sin {x^2} = 1 \Leftrightarrow {x^2} = \frac{\pi }{2} + k2\pi, \left( {k \ge 0,k \in \mathbb{Z}} \right)\)
\( \max y = \sqrt 2 - 1\) khi \(\sin {x^2} = - 1 \Leftrightarrow {x^2} = - \frac{\pi }{2} + k2\pi, \left( {k > 0,k \in \mathbb{Z}} \right)\)
c) \( y = 4\sin \sqrt x\)
Ta có: \(- 1 \le \sin \sqrt x \le 1\)
\( \Rightarrow - 4 \le 4\sin \sqrt x \le 4 \\ ⇒ -4 ≤ y ≤ 4\)
Vậy min y = - 4 khi \(\sin \sqrt x = - 1 \Leftrightarrow \sqrt x = - \frac{\pi }{2} + k2\pi, \left( {k \in \mathbb{Z},k > 0} \right)\)
max y = 4 khi \(\sin \sqrt x = 1 \Leftrightarrow \sqrt x = \frac{\pi }{2} + k2\pi, \left( {k \in \mathbb{Z},k \ge 0} \right)\)
4. Giải bài 4 trang 14 SGK Đại số & Giải tích 11 Nâng cao
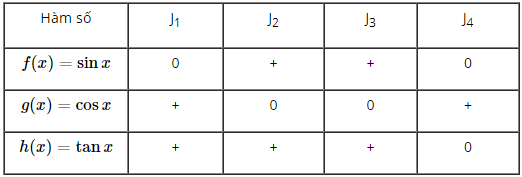
Cho các hàm số f(x) = sin x, g(x) = cos x, h(x) = tan x và các khoảng \( {J_1} = \left( {\pi ;{{3\pi } \over 2}} \right)\); \({J_2} = \left( { - {\pi \over 4};{\pi \over 4}} \right)\); \({J_3} = \left( {{{31\pi } \over 4};{{33\pi } \over 4}} \right)\); \({J_4} = \left( { - {{452\pi } \over 3};{{601\pi } \over 4}} \right)\).
Hỏi hàm số nào trong ba hàm số trên đồng biến trên khoảng J1? Trên khoảng J2? Trên khoảng J3? Trên khoảng J4? (Trả lời bằng cách lập bảng).
Phương pháp giải:
Sử dụng lí thuyết:
- Hàm số y = sin x đồng biến trên \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\)
- Hàm số y = cos x đồng biến trên \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên \(\left( {k2\pi ;\pi + k2\pi } \right)\)
- Hàm số y = tan x đồng biến trên \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right).\)
Hướng dẫn giải:
Ta có:
+) \({J_1} = \left( {\pi ;\frac{{3\pi }}{2}} \right) \subset \left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)
⇒ Hàm số y = sin x nghịch biến trên J1, hàm số y = tan x đồng biến trên J1.
\( {J_1} = \left( {\pi ;\frac{{3\pi }}{2}} \right) \subset \left( {\pi ;2\pi } \right)\)
⇒ Hàm số y = cos x đồng biến trên J1.
+) \({J_2} = \left( { - \frac{\pi }{4};\frac{\pi }{4}} \right) \subset \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
⇒ Hàm số y = sin x đồng biến trên J2, hàm số y = tan x đồng biến trên J2.
\( {J_2} = \left( { - \frac{\pi }{4};\frac{\pi }{4}} \right) = \left( { - \frac{\pi }{4};0} \right) \cup \left[ {0;\frac{\pi }{4}} \right)\)
Ta có: Hàm số y = cos x chỉ đồng biến trên \(\left( {\frac{\pi }{4};0} \right)\) và nghịch biến trên \(\left( {0;\frac{\pi }{4}} \right)\)
⇒ Hàm số y = cos x không đồng biến trên J2
+) \({J_3} = \left( {\frac{{31\pi }}{4};\frac{{33\pi }}{4}} \right) = \left( {8\pi - \frac{\pi }{4};8\pi + \frac{\pi }{4}} \right)\)
⇒ Hàm số y = sin x và hàm số y = tan x đồng biến trên J3, hàm số y = cos x không đồng biến trên J3
+) \({J_4} = \left( { - \frac{{452\pi }}{3};\frac{{601\pi }}{4}} \right) = \left( { - 150\pi - \frac{{2\pi }}{3}; - 150\pi - \frac{\pi }{4}} \right)\)
⇒ Hàm số y = sin x, y = tan x không đồng biến trên J4, hàm số y = cos x đồng biến trên J4
Ta có bảng sau, trong đó dấu “ +” có nghĩa “đồng biến”, dấu “0” có nghĩa “không đồng biến” :
5. Giải bài 5 trang 14 SGK Đại số & Giải tích 11 Nâng cao
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai? Giải thích vì sao?
a) Trên mỗi khoảng mà hàm số y = sin x đồng biến thì hàm số y = cos x nghịch biến.
b) Trên mỗi khoảng mà hàm số \(y = \sin^2 x\) đồng biến thì hàm số \(y = \cos^2 x\) nghịch biến.
Phương pháp giải:
a) Xét tính đồng biến, nghịch biến của hai hàm số trên \(\left( { - {\pi \over 2};{\pi \over 2}} \right)\).
b) - Giả sử \(y = \sin^2 x\) đồng biến trên khoảng I.
- Chứng minh \(y = \cos^2 x\) nghịch biến trên khoảng I.
Hướng dẫn giải:
a) Sai vì trên khoảng \(\left( { - {\pi \over 2};{\pi \over 2}} \right)\) hàm số y = sin x đồng biến nhưng hàm số y = cos x không nghịch biến.
b) Đúng do \({\sin ^2}x + {\cos ^2}x = 1\)
Giả sử đồng biến trên khoảng I, khi đó với \(x_1,x_2\in I \) và \(x_1<x_2 \) thì \( {\sin ^2}{x_1}< {\sin ^2}{x_2}\)
\( \Rightarrow 1 - {\sin ^2}{x_1} > 1 - {\sin ^2}{x_2}\)
\( \Rightarrow {\cos ^2}{x_1} > {\cos ^2}{x_2}\)
\( ⇒ y = \cos^2 x\) nghịch biến trên I.
6. Giải bài 6 trang 15 SGK Đại số & Giải tích 11 Nâng cao
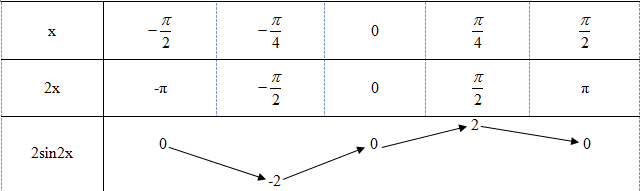
Cho hàm số y = f(x) = 2sin 2x
a. Chứng minh rằng với số nguyên k tùy ý, luôn có f(x + kπ) = f(x) với mọi x.
b. Lập bảng biến thiên của hàm số y = 2sin 2x trên đoạn \( \left[ { - {\pi \over 2};{\pi \over 2}} \right].\)
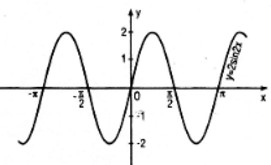
c. Vẽ đồ thị của hàm số y = 2sin 2x.
Phương pháp giải:
a) Thay x = x + kπ vào f(x).
b) Vẽ bảng biến thiên của hàm số y = 2sin 2x trên đoạn \( \left[ { - {\pi \over 2};{\pi \over 2}} \right].\)
c) Vẽ đồ thị của hàm số y = 2sin 2x dựa trên bảng biến thiên ở câu b.
Hướng dẫn giải:
a) Ta có
f(x + kπ) = 2sin 2(x + kπ)
= 2sin (2x + k2π) = 2sin 2x = f(x), \( ∀ x \in\mathbb R\)
b) Bảng biến thiên:
c)Đồ thị:
7. Giải bài 7 trang 16 SGK Đại số & Giải tích 11 Nâng cao
Xét tính chẵn – lẻ của mỗi hàm số sau:
a. \( y = \cos \left( {x - {\pi \over 4}} \right)\)
b. \( y = \tan \left| x \right|\)
c. \( y = \tan x - \sin 2x.\)
Phương pháp giải:
a) Lấy ví dụ kiểm tra, thay \(x = \frac{\pi }{4};x = - \frac{\pi }{4}\) , kiểm tra giá trị của hàm số tại các điểm này và so sánh.
b) c) Xét tính chẵn - lẻ của hàm số y = f(x):
- Tìm TXĐ D
- Nếu D là tập đối xứng, f(-x) = f(x): Hàm số chẵn.
- Nếu D là tập đối xứng, f(-x) = -f(x): Hàm số lẻ
Hướng dẫn giải:
a) \( y =f(x)= \cos \left( {x - {\pi \over 4}} \right)\)
Ta có:
\( \eqalign{ & f\left( x \right) = \cos \left( {x - {\pi \over 4}} \right)\cr&f\left( {{\pi \over 4}} \right) = 1,f\left( { - {\pi \over 4}} \right) = 0 \cr & f\left( { - {\pi \over 4}} \right) \ne f\left( {{\pi \over 4}} \right)\cr& \text{và }f\left( { - {\pi \over 4}} \right) \ne - f\left( {{\pi \over 4}} \right) \cr}\)
Nên \(y = \cos \left( {x - {\pi \over 4}} \right)\) không phải là hàm số chẵn cũng không phải là hàm số lẻ.
b) \(y =f(x)= \tan \left| x \right|\)
Tập xác định \(D =\mathbb R \backslash \left\{ {{\pi \over 2} + k\pi,k \in \mathbb Z} \right\}\)
\( x \in D ⇒ -x \in D \) và \(f(-x) = \tan |-x| = \tan |x| = f(x)\)
Do đó y = tan |x| là hàm số chẵn.
c) y = f(x) = tan x - sin 2x.
Tập xác định \(D =\mathbb R \backslash \left\{ {{\pi \over 2} + k\pi,k \in\mathbb Z} \right\}\)
\( x \in D ⇒ -x \in D\)
\(f(-x) = \tan(-x) – \sin(-2x)\)
\( = -\tan x + \sin 2x = -(\tan x – \sin 2x) = -f(x)\)
Do đó y = tan x – sin 2x là hàm số lẻ.
8. Giải bài 8 trang 16 SGK Đại số & Giải tích 11 Nâng cao
Cho các hàm số sau:
a) \(y = - {\sin ^2}x\)
b) \(y = 3{\tan ^2}x + 1\)
c) \(y = \sin x\cos x\)
d) \(y = \sin x\cos x + {{\sqrt 3 } \over 2}\cos 2x\)
Chứng minh rằng mỗi hàm số y = f(x) đó đều có tính chất: f(x + kπ) = f(x) với \(k \in\mathbb Z\), x thuộc tập xác định của hàm số f.
Phương pháp giải:
Tính f(x + kπ) và so sánh với f(x)
Hướng dẫn giải:
a) \(y = - {\sin ^2}x\)
Với \(k \in\mathbb Z\) ta có:
\( \begin{array}{l} f\left( x \right) = - {\sin ^2}x\\ = - \frac{{1 - \cos 2x}}{2} = \frac{{\cos 2x + 1}}{2}\\ \Rightarrow f\left( {x + k\pi } \right)\\ = \frac{{\cos \left[ {2\left( {x + k\pi } \right)} \right] + 1}}{2}\\ = \frac{{\cos \left( {2x + k2\pi } \right) + 1}}{2}\\ = \frac{{\cos 2x + 1}}{2}\\ = f\left( x \right) \end{array}\)
b) \(y = 3{\tan ^2}x + 1\)
Với \(k \in\mathbb Z\) ta có:
\( \eqalign{ & f\left( x \right) = 3{\tan ^2}x + 1 \cr & f\left( {x + k\pi } \right) = 3{\tan ^2}\left( {x + k\pi } \right) + 1 \cr&= 3{\tan ^2}x + 1 = f\left( x \right) \cr}\)
c) \( y = \sin x\cos x\)
Với \(k \in\mathbb Z\) ta có:
\( \eqalign{ & f\left( {x + k\pi } \right) = \sin \left( {x + k\pi } \right).\cos \left( {x + k\pi } \right) \cr&= {\left( { - 1} \right)^k}\sin x.{\left( { - 1} \right)^k}\cos x \cr & = {\left( { - 1} \right)^{2k}}\sin x\cos x\cr&= \sin x\cos x = f\left( x \right) \cr}\)
d) \(y = \sin x\cos x + {{\sqrt 3 } \over 2}\cos 2x\)
Với \(k \in\mathbb Z\) ta có:
\( \eqalign{ & f\left( x \right) = \sin x\cos x + {{\sqrt 3 } \over 2}\cos 2x \cr & f\left( {x + k\pi } \right) \cr&= \sin \left( {x + k\pi } \right)\cos \left( {x + k\pi } \right) \cr&+ {{\sqrt 3 } \over 2}\cos \left( {2x + k2\pi } \right) \cr & = {\left( { - 1} \right)^k}\sin x{\left( { - 1} \right)^k}\cos x + {{\sqrt 3 } \over 2}\cos 2x \cr&= \sin x\cos x + {{\sqrt 3 } \over 2}\cos 2x = f\left( x \right) \cr}\)
9. Giải bài 9 trang 17 SGK Đại số & Giải tích 11 Nâng cao
Cho hàm số \(y = f(x) = A\sin(ωx + \alpha)\) (A, ω và \(\alpha \) là những hằng số; A và ω khác 0). Chứng minh rằng với mỗi số nguyên k, ta có \( f\left( {x + k.{{2\pi } \over \omega }} \right) = f\left( x \right)\) với mọi x.
Phương pháp giải:
Tính \( f\left( {x + k.{{2\pi } \over \omega }} \right) \) và so sánh với f(x)
Hướng dẫn giải:
Với \(k \in \mathbb Z\) ta có :
\( \eqalign{ & f\left( {x + k.{{2\pi } \over \omega }} \right) \cr&= A\sin \left[ {\omega \left( {x + k{{2\pi } \over \omega }} \right) + \alpha } \right] \cr & = A\sin \left( {\omega x + \alpha + k2\pi } \right) \cr&= A\sin \left( {\omega x + \alpha } \right) \cr&= f\left( x \right) \cr}\)
10. Giải bài 10 trang 17 SGK Đại số & Giải tích 11 Nâng cao
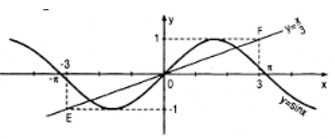
Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình \(y = {x \over 3}\) với đồ thị của hàm số y = sin x đều cách gốc tọa độ một khoảng nhỏ hơn \( \sqrt {10}\)
Phương pháp giải:
Lấy hai điểm thuộc đường thẳng \(y = {x \over 3}\).
Sử sụng bất đẳng thức tam giác suy ra điều phải chứng minh.
Hướng dẫn giải:
Đường thẳng \(y = {x \over 3}\) đi qua các điểm E(-3 ; -1) và F(3 ; 1)
Chỉ có đoạn thẳng EF của đường thẳng đó nằm trong dải \(\left\{ {\left( {x{\rm{ }};{\rm{ }}y} \right)| - 1{\rm{ }} \le {\rm{ }}y{\rm{ }} \le {\rm{ }}1} \right\}\) (dải này chứa đồ thị của hàm số y = sin x ).
Vậy các giao điểm của đường thẳng \(y = {x \over 3}\) với đồ thị của hàm số y = sin x phải thuộc đoạn EF.
Mọi điểm của đoạn thẳng này cách O một khoảng không dài hơn \(OE=OF=\sqrt {3^2 + 1^2} = \sqrt {10}\)
Rõ ràng E, F không thuộc đồ thị của hàm số y = sin x nên khoảng cách từ các giao điểm đến O nhỏ hơn \(\sqrt {10}.\)
11. Giải bài 11 trang 17 SGK Đại số & Giải tích 11 Nâng cao
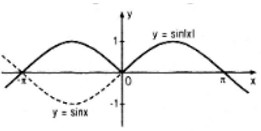
Từ đồ thị của hàm số y = sin x, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:
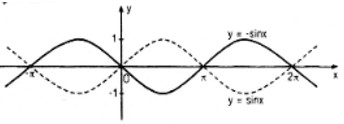
a. y = - sin x
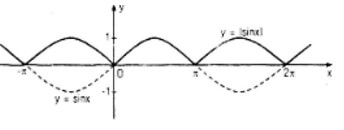
b. y = |sin x|
c. y = sin|x|
Phương pháp giải:
a) Đồ thị của hàm số y = -sin x là hình đối xứng qua trục hoành của đồ thị hàm số y = sin x
b) Sử dụng công thức: \(\left| {\sin x} \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,\sin x \ge 0} \cr { - \sin x\,\text{ nếu }\,\sin x < 0} \cr} } \right.\)
⇒ Đồ thị của hàm số y = |sin x|.
c) Sử dụng công thức \(\sin \left| x \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,x \ge 0} \cr { - \sin x\,\text{ nếu }\,x < 0} \cr} } \right.\)
⇒ Đồ thị của hàm số y = sin |x|.
Hướng dẫn giải:
a) y = - sin x
Đồ thị của hàm số y = -sin x là hình đối xứng qua trục hoành của đồ thị hàm số y = sin x
b) y = |sin x|
Ta có:
\(\left| {\sin x} \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,\sin x \ge 0} \cr { - \sin x\,\text{ nếu }\,\sin x < 0} \cr} } \right.\)
Do đó đồ thị của hàm số y = |sin x| có được từ đồ thị (C) của hàm số y = sin x bằng cách:
- Giữ nguyên phần đồ thị của (C) nằm trong nửa mặt phẳng y ≥ 0 (tức nửa mặt phẳng bên trên trục hoành kể cả bờ Ox ).
- Lấy hình đối xứng qua trục hoành của phần đồ thị (C) nằm trong nửa mặt phẳng y < 0 (tức là nửa mặt phẳng bên dưới trục hoành không kể bờ Ox );
- Xóa phần đồ thị của (C) nằm trong nửa mặt phẳng y < 0.
- Đồ thị y = |\sin x| là đường liền nét trong hình dưới đây:
c) y = sin|x|
Ta có:
\(\sin \left| x \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,x \ge 0} \cr { - \sin x\,\text{ nếu }\,x < 0} \cr} } \right.\)
Do đó đồ thị của hàm số y = sin|x| có được từ đồ thị (C) của hàm số y = sin x bằng cách:
- Giữ nguyên phần đồ thị của (C) nằm trong nửa mặt phẳng x ≥ 0 (tức nửa mặt phẳng bên phải trục tung kể cả bờ Oy ).
- Xóa phần đồ thị của (C) nằm trong nửa mặt phẳng x < 0 (tức nửa mặt phẳng bên trái trục tung không kể bờ Oy ).
- Lấy hình đối xứng qua trục tung của phần đồ thị (C) nằm trong nửa mặt phẳng x > 0
- Đồ thị y = sin|x| là đường nét liền trong hình dưới đây:
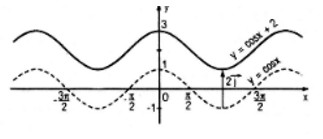
12. Giải bài 12 trang 17 SGK Đại số & Giải tích 11 Nâng cao
a) Từ đồ thị của hàm số y = cos x, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:
y = cos x + 2
\( y = \cos \left( {x - {\pi \over 4}} \right)\)
b) Hỏi mỗi hàm số đó có phải là hàm số tuần hoàn không ?
Phương pháp giải:
a) Sử dụng lý thuyết tịnh tiến đồ thị:
Cho hàm số y = f(x) có đồ thị (C). Khi đó:
+) Hàm số y = f(x) + p có được do tịnh tiến (C) lên trên p đơn vị (p > 0).
+) Hàm số y = f(x - q) có được do tịnh tiến (C) sang phải q đơn vị (q > 0).
b) Tính f(x + 2π) và so sánh với f(x)
- Nếu f(x + 2π) = f(x) thì hàm số tuần hoàn.
- Nếu f(x + 2π) \(\ne\) f(x) thì hàm số không tuần hoàn.
Hướng dẫn giải:
a) Đồ thị của hàm số y = cos x + 2 có được do tịnh tiến đồ thị của hàm số y = cos x lên trên một đoạn có độ dài bằng 2.
Đồ thị của hàm số \(y = \cos \left( {x - {\pi \over 4}} \right)\) có được do tịnh tiến đồ thị của hàm số y = cosx sang phải một đoạn có độ dài \({\pi \over 4}\)
b) Các hàm số trên đều là hàm tuần hoàn vì:
Nếu f(x) = cos x + 2 thì f(x + 2π) = cos(x + 2π) + 2 = cos x + 2 = f(x), \(∀x \in\mathbb R\)
Và nếu \(g(x) = \cos \left( {x - {\pi \over 4}} \right)\) thì:
\( g(x + 2π) = \cos \left( {x + 2\pi - {\pi \over 4}} \right) \\ =\cos \left( {x - {\pi \over 4}} \right) = g\left( x \right), ∀x \in\mathbb R\)
13. Giải bài 13 trang 17 SGK Đại số & Giải tích 11 Nâng cao
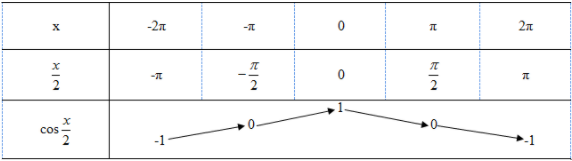
Xét hàm số \( y = f\left( x \right) = \cos {x \over 2}\)
a) Chứng minh rằng với mỗi số nguyên k, f(x + k4π) = f(x) với mọi x.
b) Lập bảng biến thiên của hàm số \(y = \cos {x \over 2}\) trên đoạn [-2π ; 2π].
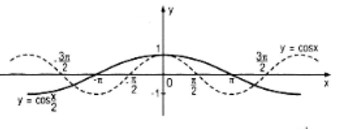
c) Vẽ đồ thị của các hàm số y = cos x và \(y = \cos {x \over 2}\) trong cùng một hệ trục tọa độ vuông góc Oxy.
d) Trong mặt phẳng tọa độ Oxy, xét phép biến hình F biến mỗi điểm (x ; y) thành điểm (x'; y') sao cho x'= 2x và y'= y. Chứng minh rằng F biến đồ thị của hàm số y = cos x thành đồ thị của hàm số \( y = \cos {x \over 2}.\)
Phương pháp giải:
a) Tính f(x + k4π) và so sánh với f(x).
b) Vẽ bảng biến thiên của hàm số \(y = \cos {x \over 2}\) trên đoạn [-2π ; 2π].
c) Dựa vào bảng biến thiên ở câu b, vẽ đồ thị hàm số \(y = \cos {x \over 2}\).
d) Tính x, y theo x', y' và thế vào y = cos x.
Hướng dẫn giải:
a) \(f\left( {x + k4\pi } \right) = \cos \frac{{x + k4\pi }}{2}\)
\( = \cos \left( {{x \over 2} + k2\pi } \right) = \cos {x \over 2} = f\left( x \right)\)
b) Bảng biến thiên:
c) Đồ thị của các hàm số y = cos x và \(y = \cos {x \over 2}\) trong cùng một hệ trục tọa độ vuông góc Oxy.
d) Ta có:
\( \left\{ \begin{array}{l} x' = 2x\\ y' = y \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = \frac{{x'}}{2}\\ y =y' \end{array} \right.\)
Do đó \(y = \cos x \Leftrightarrow y' = \cos {{x'} \over 2}.\)
Do đó phép biến đổi xác định bởi (x ; y) ↦ (x' ; y') sao cho x' = 2x, y'= y biến đồ thị hàm số y = cos x thành đồ thị hàm số \( y = \cos {x \over 2}.\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 11 Nâng cao Bài 2: Phương trình lượng giác cơ bản
- doc Giải bài tập SGK Toán 11 Nâng cao Bài 3: Một số dạng phương trình lượng giác cơ bản
- doc Giải bài tập SGK Toán 11 Nâng cao Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác



.PNG)