Giải bài tập SGK Toán 11 Chương 3 Bài 3: Cấp số cộng
Phần hướng dẫn giải bài tập Cấp số cộng sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Đại số và Giải tích 11 Cơ bản-Nâng cao.
Mục lục nội dung

1. Giải bài 1 trang 97 SGK Đại số & Giải tích 11
Trong các dãy số sau đây, dãy số nào là cấp số cộng? Tính số hạng đầu và công sai của nó:
a) \(u_n = 5 - 2n\)
b) \(u_n =\frac{n}{2}-1\)
c) \(u_n = 3^n\)
d) \(u_n =\frac{7-3n}{2}\)
Phương pháp giải
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn) trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Ta chứng minh \({u_{n + 1}} - {u_n} = const\).
Hướng dẫn giải
Câu a
Ta có \(u_{n+1}-u_n= 5-2(n+1)-(5-2n)=-2\Leftrightarrow u_{n+1}=u_n+(-2).\)
⇒ (un) là cấp số cộng với u1 = 3 và d = -2.
Câu b
Ta có \(u_{n+1}-u_n= \left ( \frac{n+1}{2} -1 \right )-\left ( \frac{n}{2} -1\right ) =\frac{1}{2}\Leftrightarrow u_{n+1}=u_n+\frac{1}{2}\) ⇒ (un) là cấp số cộng với \(u_1 = \frac{1}{2}\) và \(d = \frac{1}{2}\).
Câu c
Ta có: \({u_{n + 1}} - {u_n} = {3^{n + 1}} - {3^n} = {3.3^n} - {3^n} = {2.3^n}\)
Vậy: (un) không phải là một cấp số cộng.
Câu d
Ta có \(u_{n+1}-u_n=\frac{7-(3n+3)}{2}-\frac{7-3n}{2}=-\frac{3}{2}\)
\(\Leftrightarrow u_{n+1}=u_n+\left ( -\frac{3}{2} \right )\)
⇒ (un) là cấp số cộng với u1 = 2 và \(d=-\frac{3}{2}.\)
2. Giải bài 2 trang 97 SGK Đại số & Giải tích 11
Tìm số hạng đầu và công sai của các cấp số cộng sau, biết:
a) \(\left\{\begin{matrix} u_{1}-u_{3}+u_{5}=10\\ u_{1}+u_{6=17} \end{matrix}\right.\)
b) \(\left\{\begin{matrix} u_{7}-u_{3}=8\\ u_{2}.u_{7}=75 \end{matrix}\right.\)
Phương pháp giải
Sử dụng công thức SHTQ: \(u_n= u_1+ (n – 1)d\).
Hướng dẫn giải
Câu a
Theo bài ra ta có:
\(\left\{\begin{matrix} u_{1}-(u_{1}+2d)+(u_{1}+4d)=10\\ u_{1}+(u_{1}+5d )=17 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} u_{1}+2d=10\\ 2u_{1}+5d = 17 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} u_1=16\\ d=-3 \end{matrix}\right.\)
Câu b
Từ hệ đã cho ta có:
\(\left\{\begin{matrix} u_{1}+6d-(u_{1}+2d) =8\\ (u_{1}+d)(u_{1}+6d)=75 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 4d =8\\ (u_{1}+d)(u_{1}+6d)=75 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} d=2\\ (u_1+2)(u_1+12)=75 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} d=2\\ u^2_1+14u-1-51=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} d=2\\ \\ \bigg \lbrack \begin{matrix} u_1=3\\ u_1=-17 \end{matrix} \end{matrix}\right.\)
Vậy có hai cặp thoả mãn là: \(\left\{\begin{matrix} d=2\\ u_1=3 \end{matrix}\right.\) và \(\left\{\begin{matrix} d=2\\ u_1=-17 \end{matrix}\right.\)
3. Giải bài 3 trang 97 SGK Đại số & Giải tích 11
Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng \(u_1, n, d, u_n, S_n.\)
a) Hãy viết các hệ thức liên hệ giữa các đại lượng để có thể tìm được các đại lượng còn lại?
b) Lập bảng theo mẫu sau và điền vào chỗ trống thích hợp:
|
u1 |
d |
un |
n |
Sn |
|
-2 |
|
55 |
20 |
|
|
|
-4 |
|
15 |
120 |
|
3 |
\(\frac{4}{{27}}\) |
7 |
|
|
|
|
|
17 |
12 |
72 |
|
2 |
-5 |
|
|
-205 |
Phương pháp giải
Sử dụng các công thức:
\(\begin{array}{l}
{u_n} = {u_1} + \left( {n - 1} \right)d\\
{S_n} = n{u_1} + \frac{{n\left( {n - 1} \right)}}{2}d
\end{array}\)
Hướng dẫn giải
Câu a
Các hệ thức liên hệ giữa các đại lượng u1, d, n, un, Sn.
\(u_n=u_1+(n-1)d\) với \(n\geq 2\)
\(S_n=\frac{n(n_1+u_n)}{2}=nu_1+\frac{n(n-1)}{2}d\)
Phải biết ít nhất ba đại lượng trong năm đại lượng nói trên để tính được các đại lượng còn lại.
Câu b
Thực chất đây là năm bài tập nhỏ, mỗi bài ứng với các dữ liệu ở một dòng. Học sinh phải giải từng bài nhỏ rồi mới điền kết quả.
Dòng đầu: Biết \({u_1} = - 2;{u_{20}} = 55\). Tìm d và \({S_{20}}\).
Ta có \({u_{20}} = {u_1} + 19d\)
\(\Leftrightarrow 55 = - 2 + 19d \Leftrightarrow d = 3\)
\({S_{20}} = \frac{{20\left( {{u_1} + {u_{20}}} \right)}}{2} \) \(= \frac{{20.\left( { - 2 + 55} \right)}}{2} = 530\)
Dòng 2: Biết \(d = - 4;\,\,{S_{15}} = 120\), tìm \({u_1}\) và \({u_{15}}\).
Ta có \({S_{15}} = 15{u_1} + \frac{{15.\left( {15 - 1} \right)}}{2}.d \)
\(\Leftrightarrow 120 = 15.{u_1} + 105.\left( { - 4} \right) \)
\(\Leftrightarrow 15{u_1} = 540 \Leftrightarrow {u_1} = 36\)
\( \Rightarrow {u_{15}} = {u_1} + 14d = 36 + 14.\left( { - 4} \right) = - 20\)
Dòng 3: Biết \({u_1} = 3;\,\,d = {4 \over {27}};\,\,{u_n} = 7\). Tìm n và tính \({S_n}\).
Ta có \({u_n} = {u_1} + \left( {n - 1} \right)d \)
\(\Leftrightarrow 7 = 3 + \left( {n - 1} \right).{4 \over {27}} \Leftrightarrow n = 28\)
\({S_{28}} = 28{u_1} + \frac{{28.\left( {28 - 1} \right)}}{2}.d \)
\(= 28.3 + 378.\frac{4}{{27}} = 140\)
Dòng 4: Biết \({u_{12}} = 17\) và \({S_{12}} = 72\). Tìm \({u_1}\) và \(d\).
\(\begin{array}{l}
{S_{12}} = \frac{{12\left( {{u_1} + {u_{12}}} \right)}}{2}\\
\Leftrightarrow 72 = \frac{{12\left( {{u_1} + 17} \right)}}{2}\\
\Leftrightarrow {u_1} + 17 = 12\\
\Leftrightarrow {u_1} = - 5\\
{u_{12}} = {u_1} + 11d\\
\Leftrightarrow 17 = - 5 + 11d\\
\Leftrightarrow 22 = 11d \Leftrightarrow d = 2
\end{array}\)
Dòng 5: Biết \({u_1} = 2;d = - 5\) và \({S_n} = - 205\). Tìm n và tính \({u_n}\).
Ta có
\(\begin{array}{l}
{S_n} = n{u_1} + \frac{{n\left( {n - 1} \right)}}{2}d\\
\Leftrightarrow - 205 = n.2 + \frac{{n\left( {n - 1} \right)}}{2}.\left( { - 5} \right)\\
\Leftrightarrow - 410 = 4n - 5n\left( {n - 1} \right)\\
\Leftrightarrow 5{n^2} - 9n - 410 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
n = 10\\
n = - \frac{{41}}{5}\left( {loai} \right)
\end{array} \right.\\
\Rightarrow n = 10\\
\Rightarrow {u_{10}} = {u_1} + 9d\\
= 2 + 9.\left( { - 5} \right) = - 43
\end{array}\)
Vậy ta điền được bảng như sau
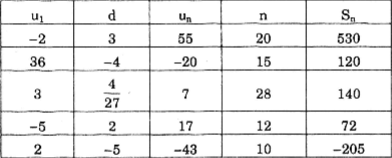
4. Giải bài 4 trang 98 SGK Đại số & Giải tích 11
Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân 0,5 m. Cầu thang đi từ tầng một lên tầng 2 gồm 21 bậc, mỗi bậc cao 18 cm.
a) Hãy viết công thức để tìm độ cao của một bậc tuỳ ý so với mặt sân
b) Tính độ cao của sàn tầng hai so với mặt sân
Phương pháp giải
Đây là một bài toán cấp số cộng.
- Xác định số dạng thức nhất \(u_1\).
- Xác định công sai \(d\).
Sử dụng công thức số hạng tổng quát: \(u_n=u_1+(n-1)d\)
Hướng dẫn giải
Câu a
Đây là một bài toán cấp số cộng với \(u_1=0,5+0,18\) (chiều cao từ mặt sân đến bậc một) và \(d=0,18\)
Gọi chiều cao của bậc thứ \(n\) so với mặt sân là \(h_n\)
Ta có: \( h_n= 0,5 +0,18 + (n-1).0,18\) \(=0,5+0,18n(m)\)
Câu b
Chiều cao mặt sàn tầng hai so với mặt sân là \(h_{21}= 0,5 + 21.0,18 = 4,28 (m)\).
5. Giải bài 5 trang 98 SGK Đại số & Giải tích 11
Từ giờ đến 12 giờ trưa, đồng hồ đánh bao nhiêu tiếng, nếu nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ
Phương pháp giải
Sử dụng công thức tính tổng của cấp số cộng: \({S_n} = \frac{{\left( {{u_1} + {u_n}} \right)n}}{2}\)
Hướng dẫn giải
Lúc 1 giờ đồng hồ đánh 1 tiếng chuông.
Lúc 2 giờ đồng hồ đánh 2 tiếng chuông
......
Lúc 12 giờ trưa đồng hồ đánh 12 tiếng chuông.
Do đó, từ 0 giờ đến 12 giờ trưa, đồng hồ đánh số tiếng chuông là:
\(S = 1 + 2 + 3 +....+ 12\).
Đây là tổng của \(12\) số hạng của cấp số cộng có \(u_1= 1, u_{12}= 12\).
Do đó áp dụng công thức tính tổng của cấp số cộng ta có \(S = \dfrac{(1+12).12}{2} = 78\).
Vậy đồng hồ đánh \(78\) tiếng chuông.
Tham khảo thêm
- doc Giải bài tập SGK Toán 11 Chương 3 Bài 1: Phương pháp quy nạp toán học
- doc Giải bài tập SGK Toán 11 Chương 3 Bài 2: Dãy số
- doc Giải bài tập SGK Toán 11 Chương 3 Bài 4: Cấp số nhân
- doc Giải bài tập SGK Toán 11 Ôn tập chương 3: Dãy số, Cấp số cộng và Cấp số nhân



