Giải bài tập SBT Vật lý 11 Bài 1: Điện tích. Định luật Cu-lông
Dưới đây là nội dung Hướng dẫn Giải bài tập SBT Lý 11 Bài 1 nhằm giúp các em học sinh nắm vững kiến thức về điện tích và định luật Cu-lông. Mời các em cùng theo dõi.
Mục lục nội dung
1. Giải bài 1.1 trang 3 SBT Vật lý 11
2. Giải bài 1.2 trang 3 SBT Vật lý 11
3. Giải bài 1.3 trang 3 SBT Vật lý 11
4. Giải bài 1.4 trang 4 SBT Vật lý 11
5. Giải bài 1.5 trang 4 SBT Vật lý 11
6. Giải bài 1.6 trang 4 SBT Vật lý 11
7. Giải bài 1.7 trang 4 SBT Vật lý 11
8. Giải bài 1.8 trang 5 SBT Vật lý 11

Giải bài tập SBT Vật lý 11 Bài 1: Điện tích. Định luật Cu-lông
1. Giải bài 1.1 trang 3 SBT Vật lý 11
Nhiễm điện cho một thanh nhựa rồi đưa nó lại gần hai vật M và N. Ta thấy thanh nhựa hút cả hai vật M và N. Tình huống nào dưới đây chắc chắn không thể xảy ra?
A. M và N nhiễm điện cùng dấu.
B. M và N nhiễm điện trái dấu.
C. M nhiễm điện, còn N không nhiễm điện.
D. Cả M và N đều không nhiễm điện.
Phương pháp giải
Vận dụng tính chất nhiễm điện của vật: Hai điện tích trái dấu thì hút nhau, cùng dấu thì đẩy nhau.
Hướng dẫn giải
- Thanh nhựa hút cả hai vật M và N nên M và N nhiễm điện trái dấu.
- Đáp án B
2. Giải bài 1.2 trang 3 SBT Vật lý 11
Một hệ cô lập gồm ba điện tích điểm, có khối lượng không đáng kể, nằm cân bằng với nhau. Tình huống nào dưới đây có thể xảy ra ?
A. Ba điện tích cùng dấu nằm ở ba đỉnh của một tam giác đều.
B. Ba điện tích cùng dấu nằm trên một đường thẳng.
C. Ba điện tích không cùng dấu nằm tại ba đỉnh của một tam giác đều.
D. Ba điện tích không cùng dấu nằm trên một đường thẳng.
Phương pháp giải
Để trả lời câu hỏi này cần nắm được nội dung lý thuyết về các điện tích điểm
Hướng dẫn giải
- Ba điện tích không cùng dấu nằm trên một đường thẳng.
- Đáp án D.
3. Giải bài 1.3 trang 3 SBT Vật lý 11
Nếu tăng khoảng cách giữa hai điện tích điểm lên 3 lần thì lực tương tác tĩnh điện giữa chúng sẽ
A. tăng lên 3 lần.
B. giảm đi 3 lần.
C. tăng lên 9 lần.
D. giảm đi 9 lần.
Phương pháp giải
Áp dụng công thức định luật Cu-lông:
F=kq1q2r2F=kq1q2r2 để rút ra tỉ lệ giữa lực điện và khoảng cách các điện tích
Hướng dẫn giải
- Nếu tăng khoảng cách giữa hai điện tích điểm lên 3 lần thì lực tương tác tĩnh điện giữa chúng sẽ giảm đi 9 lần.
- Đáp án D.
4. Giải bài 1.4 trang 4 SBT Vật lý 11
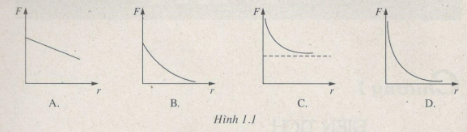
Đồ thị nào trong Hình 1.1 có thể biểu diễn sự phụ thuộc của lực tương tác giữa hai điện tích điểm vào khoảng cách giữa chúng ?
Phương pháp giải
Dựa theo định luật Cu-lông ta thấy lực điện F tỉ lệ nghịch với bình phương khoảng cách (r2) để chọn đồ thì phù hợp
Hướng dẫn giải
- Đồ thị hình D biểu diễn sự phụ thuộc của lực tương tác giữa hai điện tích điểm vào khoảng cách giữa chúng.
- Đáp án D
5. Giải bài 1.5 trang 4 SBT Vật lý 11
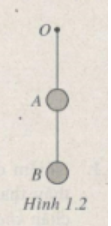
Hai quả cầu A và B có khối lượng m1 và m2 được treo vào một điểm O bằng hai sợi dây cách điện OA và AB (Hình 1.2). Tích điện cho hai quả cầu. Lực căng T của sợi dây OA sẽ thay đổi như thế nào so với lúc chúng chưa tích điện ?
A. T tăng nếu hai quả cầu tích điện trái dấu.
B. T giảm nếu hai quả cầu tích điện cùng dấu.
C. T thay đổi
D. T không đổi.
Phương pháp giải
Lực căng dây chỉ phụ thuộc vào khối lượng vật treo và tính chất dây, không phụ thuộc vào điện tích của vật
Hướng dẫn giải
- Lực căng T của sợi dây OA không đổi.
- Đáp án D.
6. Giải bài 1.6 trang 4 SBT Vật lý 11
a) Tính lực hút tĩnh điện giữa hạt nhân trong nguyên tử heli với một êlectron trong lớp vỏ nguyên tử. Cho rằng êlectron này nằm cách hạt nhân 2,94.10-11m.
b) Nếu êlectron này chuyển động tròn đều quanh hạt nhân với bán kính quỹ đạo như đã cho ở trên thì tốc độ góc của nó sẽ là bao nhiêu ?
c) So sánh lực hút tĩnh điện với lực hấp dẫn giữa hạt nhân và êlectron.
Điện tích của êlectron: -1,6.10-19C. Khối lượng của êlectron : 9,1.10-31kg.
Khối lượng của hạt nhân heli 6,65.10-27kg. Hằng số hấp dẫn 6,67.1011m3/kg.s2.
Phương pháp giải
a) Áp dụng công thức:
F=kq1q2r2F=kq1q2r2để tính lực hút tĩnh điện
b) Dựa vào biểu thức lực hướng tâm để tính tốc độ góc theo công thức:
ω=√Fmrω=√Fmr
c) Tính lực hấp dẫn giữa hạt nhân và êlectron theo công thức:
Fhd=Gmhn.mer2Fhd=Gmhn.mer2
⇒ Ta lập tỉ số: F/Fhd để so sánh hai lực.
Hướng dẫn giải
a) Lực hút tĩnh điện giữa hạt nhân trong nguyên tử Heli với một electron trong lớp vỏ nguyên tử:
F=k|q1q2|r2=k|q.e|r2=9.109|3,2.10−19.(−1,6.10−19)|(2,94.10−11)2=5,33.10−7N
b) Electron khi chuyển động xung quanh hạt nhân thì khi đó lực hút tĩnh điện đóng vai trò là lực hướng tâm
Ta có: F=Fht=maht=mω2r
Ta suy ra tốc độ góc của electron là:
ω=√Fmr=√5,33.10−119,1.10−31.2,94.10−11=1,41.1017(rad/s)
c) Lực hấp dẫn giữa hạt nhân và electron là:
Fhd=Gmhn.mer2=6,67.1011.6,65.10−27.9,1.10−31(2,94.10−11)2=4,67.10−24N
Ta có: FFhd=5,33.10−74,67.10−24=1,14.1017
Suy ra lực hút tĩnh điện gấp 1,14.1017 lần lực hấp dẫn giữa hạt nhân và electron
7. Giải bài 1.7 trang 4 SBT Vật lý 11
Hai quả cầu nhỏ giống nhau bằng kim loại, có khối lượng 5g, được treo vào cùng một điểm O bằng hai sợi chỉ không dãn, dài 10cm. Hai quả cầu tiếp xúc với nhau. Tích điện cho một quả cầu thì thấy hai quả cầu đẩy nhau cho đến khi hai dây treo hợp với nhau một góc 600.
Tính điện tích mà ta đã truyền cho các quả cầu. Lấy g=10 m/s2.
Phương pháp giải
Để tính điện tích quả cầu, ta làm theo cách sau:
- Tính lực đẩy giữa hai quả cầu theo công thức:
F=kq24r2
- Dựa vào hình vẽ, tính tỉ số giữa F và P theo công thức:
tanα2=FP
- Áp dụng công thức:
q=±2ℓ√mgktanα2 để tính điện tích quả cầu
Hướng dẫn giải
- Điện tích q mà ta truyền cho các quả cầu sẽ phân bố đều cho hai quả cầu. Mỗi quả cầu mang một điện tích q/2.
- Hai quả cầu sẽ đẩy nhau với một lực là
F=kq24r2
- Vì góc giữa hai dây treo α = 60° nên r = l= 10 cm. Mỗi quả cầu sẽ nằm cân bằng dưới tác dụng của ba lực: lực căng
→T của sợi dây, lực điện →F và trọng lực →P của quả cầu (Hình 1.1G)
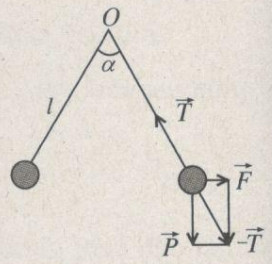
- Điện tích mà ta đã truyền cho các quả cầu là:
tanα2=FP=kq24ℓ2mg⇒q=±2ℓ√mgktanα2q≈±3,58.10−7C
8. Giải bài 1.8 trang 5 SBT Vật lý 11
Một hệ điện tích có cấu tạo gồm một ion dương +e và hai ion âm giống nhau nằm cân bằng. Khoảng cách giữa hai ion âm là α. Bỏ qua trọng lượng của các ion.
a) Hãy cho biết cấu trúc của hệ và khoảng cách giữa ion dương và ion âm (theo a).
b) Tính điện tích của một ion âm (theo e)
Phương pháp giải
a) Dựa vào lí thuyết về điện tích điểm để giải thích cấu trúc hệ
b) Áp dụng các công thức:
- Fd=kq2a2 để tính lực đẩy giữa hai ion âm
- Fh=k4|q|ea2 lực hút giữa ion dương và ion âm
- Vận dụng tính cân bằng: Fđ = Fh để tìm giá trị điện tích của mỗi ion
Hướng dẫn giải
a) Trong trạng thái cân bằng, những lực điện tác dụng lên mỗi ion cân bằng lẫn nhau.
- Điều đó có nghĩa là tất cả các lực phải có cùng một giá hay ba ion phải nằm trên cùng một đường thẳng.
- Mặt khác, hai ion âm phải nằm đối xứng với nhau ở hai bên ion dương (Hình 1.2 G), thì lực điện do chúng tác dụng lên ion dương mới có thể cân bằng nhau.
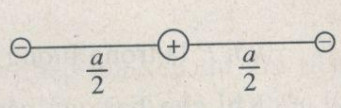
b) Xét sự cân bằng của một ion âm.
- Cường độ của lực đẩy giữa hai ion âm :
Fd=kq2a2
- Cường độ của lực hút giữa ion dương và ion âm :
Fh=k4|q|ea2
- Vì Fđ = Fh, nên |q| = 4e.
⇒ Kết quả là q = - 4e
9. Giải bài 1.9 trang 5 SBT Vật lý 11
Một hệ gồm ba điện tích dương q giống nhau và một điện tích Q nằm cân bằng. Ba điện tích q nằm tại ba đỉnh của một tam giác đều. Xác định dấu, độ lớn (theo q) và vị trí của điện tích Q.
Phương pháp giải
- Vận dụng tính chất: cùng dấu thì đẩy nhau, khác dấu thì hút nhau để xác định dấu của điện tích Q
- Áp dụng công thức tính lực điện tại C để:
+ Tìm khoảng cách theo công thức:
r=23a√32
+ Tìm độ lớn điện tích Q theo công thức:
|Q|=√33q
Hướng dẫn giải
Xét sự cân bằng của điện tích q nằm tại đỉnh C chẳng hạn của tam giác đều ABC cạnh a.
- Lực đẩy của mỗi điện tích q nằm ở A hoặc B tác dụng lên điện tích ở C :
F=kq2a2
- Hợp lực của hai lực đẩy có phương nằm trên đường phân giác của góc C, chiều hướng ra
- Muốn điện tích tại c nằm cân bằng thì phải có một lực hút cân bằng với lực đẩy
⇒ Như vậy điện tích Q phải trái dấu với q (Q phải là điện tích âm) và phải nằm trên đường phân giác của góc C.
Tương tự, Q cũng phải nằm trên các đường phân giác của các góc A và B. Do đó, Q phải nằm tại trọng tâm của tam giác ABC.
- Khoảng cách từ Q đến C sẽ là:
Fd=F√3=kq2a2√3
⇒ r=23a√32=a√33
- Cường độ của lực hút là:
Fh=k3q|Q|a2Fd=Fh⇒|Q|=√33q=0,577q
Vậy Q = - 0,577q.
10. Giải bài 1.10 trang 5 SBT Vật lý 11
Hai quả cầu kim loại nhỏ, giống hệt nhau, chứa các điện tích cùng dấu q1 và q2, được treo vào chung một điểm O bằng hai sợi dây chỉ mảnh, không dãn, dài bằng nhau. Hai quả cầu đẩy nhau và góc giữa hai dây treo là 60°. Cho hai quả cầu tiếp xúc với nhau, rồi thả ra thì chúng đẩy nhau mạnh hơn và góc giữa hai dây treo bây giờ là 900. Tính tỉ số q1q2.
Phương pháp giải
Để tính tỉ số q1q2 ta làm như sau:
- Dựa vào hình vẽ rút ra công thức giữa lực điện và trọng lượng là:
tan30o=F1P=kq1q2Pℓ2
- Tính lực đẩy sau khi hai quả cầu trao đổi điện tích theo công thức:
F2=k(q1+q2)28ℓ2
- Vận dụng tính chất cân bằng lực, giải phương trình và rút ra giá trị tỉ số q1/q2 là 11,77 hoặc 0,085
Hướng dẫn giải
Gọi l là chiều dài của dây treo. Khi chưa trao đổi điện tích với nhau thì khoảng cách giữa hai quả cầu là l.
- Lực đẩy giữa hai quả cầu là :
F1=kq1q2ℓ2
- Tương tư hình 1.1G, ta có :
tan30o=F1P=kq1q2Pℓ2 (1) với P là trọng lượng quả cầu.

- Khi cho hai quả cầu trao đổi điện tích với nhau thì mỗi quả cầu mang điện tích
q=q1+q22
- Chúng vẫn đẩy nhau và khoảng cách giữa chúng bây giờ là ℓ√2
- Lực đẩy giữa chúng bây giờ là :
F2=k(q1+q2)28ℓ2
- Tương tự như trên, ta có:
tan450=F2P=k(q1+q2)28Pℓ2 (2)
- Từ (1) và (2) suy ra:
8√3q1q2=(q1+q2)2
- Chia hai vế cho q2/2 ta có:
8√3q1q2=(q1q2+1)2
- Đặt q1q2=x ta có phương trình:
x2+(2−8√3)x+1=0⇔x2−11,86x+1=0
Các nghiệm của phương trình này là x1 = 11,77 và x2 = 0,085
⇒ Tỉ số q1/q2 là 11,77 hoặc 0,085
Tham khảo thêm
- doc Giải bài tập SBT Vật Lí 11 Bài 2: Thuyết Êlectron. Định luật bảo toàn điện tích
- doc Giải bài tập SBT Vật Lí 11 Bài 3: Điện trường và cường độ điện trường. Đường sức điện
- doc Giải bài tập SBT Vật Lí 11 Bài 4: Công của lực điện
- doc Giải bài tập SBT Vật Lí 11 Bài 5: Điện thế. Hiệu điện thế
- doc Giải bài tập SBT Vật Lí 11 Bài 6: Tụ điện




