Giải bài tập SBT Vật Lí 12 Bài tập cuối chương 4: Dao động và sóng điện từ
Ban biên tập eLib xin giới thiệu nội dung hướng dẫn Giải bài tập SBT Vật Lý 12 nhằm giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức chương IV. Mời các em cùng theo dõi.
Mục lục nội dung
1. Giải bài IV.1 trang 61 SBT Vật lý 12
2. Giải bài IV.2 trang 61 SBT Vật lý 12
3. Giải bài IV.3 trang 62 SBT Vật lý 12
4. Giải bài IV.4 trang 62 SBT Vật lý 12
5. Giải bài IV.5 trang 62 SBT Vật lý 12
6. Giải bài IV.6 trang 62 SBT Vật lý 12
7. Giải bài IV.7 trang 62 SBT Vật lý 12
8. Giải bài IV.8 trang 63 SBT Vật lý 12
9. Giải bài IV.9 trang 63 SBT Vật lý 12
10. Giải bài IV.10 trang 63 SBT Vật lý 12
11. Giải bài IV.11 trang 63 SBT Vật lý 12

1. Giải bài IV.1 trang 61 SBT Vật lý 12
Mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm 10−4H và tụ điện có điện dung C. Biết tần số dao động riêng của mạch là 100kHz. Lấy π2=10.Giá trị của C là
A. 0,25F. B. 25nF.
C. 0,025F. D. 250nF.
Phương pháp giải
Áp dụng công thức tính tần số:
\({f = \frac{1}{{2\pi \sqrt {LC} }}}\)
Hướng dẫn giải
- Ta có tần số
\(\begin{array}{*{20}{l}} {f = \frac{1}{{2\pi \sqrt {LC} }}}\\ { \Rightarrow C = \frac{1}{{4{\pi ^2}{f^2}L}}}\\ { = \frac{1}{{4{\pi ^2}{{({{100.10}^3})}^2}{{.10}^{ - 4}}}}}\\ { = {{25.10}^{ - 9}}(F) = 25(nF)} \end{array}\)
- Chọn B
2. Giải bài IV.2 trang 61 SBT Vật lý 12
Một mạch dao động gồm một cuộn cảm thuần có độ tự cảm xác định và một tụ điện là tụ xoay, có điện dung thay đổi được theo quy luật hàm số bậc nhất của góc xoay α của bản linh động. Khi α=00, tần số dao động riêng của mạch là 3MHz. Khi α=1200, tần số dao động riêng của mạch là 1MHz. Để mạch có tần số dao động riêng bằng 1,5MHz thì α bằng
A. 900 B. 300
C. 450 D. 600
Phương pháp giải
- Vận dụng công thức tính điện dung:
+ \(C = a\alpha + b(F)(1)\)
+ \(f = \frac{1}{{2\pi \sqrt {LC} }} \Rightarrow C \sim \frac{1}{{{f^2}}}(2)\)
- Suy ra công thức tính tần số:
\(\frac{1}{{{f^2}}} = \frac{1}{{135}}\alpha + \frac{1}{9}(MHz)\)
Hướng dẫn giải
- Tụ điện xoay tụ có dạng:
\(C = a\alpha + b(F)(1)\)
- Lại có:
\(f = \frac{1}{{2\pi \sqrt {LC} }} \Rightarrow C \sim \frac{1}{{{f^2}}}(2)\)
- Từ (1), (2) suy ra dạng của tần số là:
\(\frac{1}{{{f^2}}} = {a_1}\alpha + {b_1}\)
- Theo đề bài, ta có hệ:
\(\left\{ \begin{array}{l} \frac{1}{{{3^2}}} = {a_1}.0 + {b_1}\\ \frac{1}{{{1^2}}} = {a_1}.120 + {b_1} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {a_1} = \frac{1}{{135}}\\ {b_1} = \frac{1}{9} \end{array} \right.\)
⇒ \(\frac{1}{{{f^2}}} = \frac{1}{{135}}\alpha + \frac{1}{9}(MHz)\)
- Khi f = 1,5MHz ⇒α = 450
⇒ Chọn C
3. Giải bài IV.3 trang 62 SBT Vật lý 12
Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại trên một bản tụ điện là 4√2μC và cường độ dòng điện cực đại trong mạch là 0,5π√2A. Thời gian ngắn nhất để điện tích trên một bản tụ điện giảm từ giá trị cực đại đến nửa giá trị cực đại là
A. 8/3μs. B. 4/3μs.
C. 2/3μs. D. 16/3μs.
Phương pháp giải
- Sử dụng công thức:
I0= Q0ω ⇒ ω ⇒ T
- Sử dụng vòng tròn lượng giác để tính thời gian ngắn nhất để điện tích trên một bản tụ điện giảm từ giá trị cực đại đến nửa giá trị cực đại
Hướng dẫn giải
- Ta có:
\(\begin{array}{*{20}{l}} {{I_0} = {Q_0}\omega }\\ { \Rightarrow \omega = \frac{{{I_0}}}{{{Q_0}}} = \frac{{0,5\pi \sqrt 2 }}{{4\sqrt 2 {{.10}^{ - 6}}}}}\\ { = 125000\pi (rad/s)}\\ { \Rightarrow T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{125000\pi }}}\\ { = {{1,6.10}^{ - 5}}(s)} \end{array}\)
- Vòng tròn lượng giác:
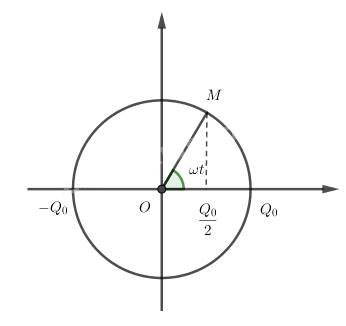
- Từ hình ta có:
\(\begin{array}{*{20}{l}} {\cos \omega t = \frac{{{Q_0}}}{{\frac{{{Q_0}}}{2}}} = \frac{1}{2}}\\ { \Rightarrow \omega t = \frac{\pi }{3} = \frac{{2\pi }}{T}}\\ { \Rightarrow t = \frac{T}{6} = \frac{{{{1,6.10}^{ - 5}}}}{6} = \frac{8}{3}{{.10}^{ - 6}}s}\\ { = \frac{8}{3}\mu s} \end{array}\)
- Chọn A
4. Giải bài IV.4 trang 62 SBT Vật lý 12
Khi nói về sóng điện từ, phát biểu nào sau đây là sai?
A. Sóng điện từ mang năng lượng.
B. Sóng điện từ là sóng ngang.
C. Sóng điện từ tuân theo các quy luật giao thoa, nhiễu xạ.
D. Sóng điện từ không truyền được trong chân không.
Phương pháp giải
Sử dụng lí thuyết của sóng điện từ
Hướng dẫn giải
- D sai vì: Sóng điện từ truyền được trong chân không
- Chọn D
5. Giải bài IV.5 trang 62 SBT Vật lý 12
Khi nói về sóng điện từ, phát biểu nào sau đây là sai?
A. Dao động của điện trường và của từ trường tại một điểm luôn luôn đồng pha với nhau.
B. Vectơ cường độ điện trường \(\vec E\) cùng phương với vectơ cảm ứng từ \(\vec B\).
C.Sóng điện từ lan truyền được trong chân không.
D. Sóng điện từ là sóng ngang và mang theo năng lượng.
Phương pháp giải
Vectơ cường độ điện trường \(\vec E\) không cùng phương với vectơ cảm ứng từ \(\vec B\).
Hướng dẫn giải
- B sai vì: Vectơ cường độ điện trường \(\vec E\), vectơ cảm ứng từ \(\vec B\) và véctơ vận tốc tạo với nhau một tam diện thuận.
- Chọn B
6. Giải bài IV.6 trang 62 SBT Vật lý 12
Một mạch dao động LC đang có dao động điện từ tự do với tần số góc ω. Gọi q0 là điện tích cực đại của một bản tụ điện. Bỏ qua sự tiêu hao năng lượng trong mạch, cường độ dòng điện cực đại trong mạch là
A. I0= q0ω2. B. I0= q0/ω2.
C. I0=q0ω. D. I0= q0/ω.
Phương pháp giải
Sử dụng công thức I0 = q0ω
Hướng dẫn giải
- Ta có I0 = q0ω
- Chọn C
7. Giải bài IV.7 trang 62 SBT Vật lý 12
Khi một mạch dao động lí tưởng (gồm cuộn cảm thuần và tụ điện) hoạt động thì
A. ở mọi thời điểm, trong mạch chỉ có năng lượng điện trường.
B. cảm ứng từ trong cuộn dây tỉ lệ nghịch với cường độ dòng điện qua cuộn dây.
C. cường độ điện trường trong tụ điện tỉ lệ nghịch với điện tích của tụ điện.
D. ở thời điểm năng lượng điện trường của mạch cực đại thì năng lượng từ trường của mạch bằng 0.
Phương pháp giải
Cơ năng không đổi và bằng tổng của động năng, thế năng của vật
Hướng dẫn giải
- Ta có: W= Wt+Wd= const
- Vậy ở thời điểm năng lượng điện trường của mạch cực đại thì năng lượng từ trường của mạch bằng 0.
- Chọn D
8. Giải bài IV.8 trang 63 SBT Vật lý 12
Sóng điện từ khi truyền từ không khí vào nước thì
A. tốc độ truyền sóng và bước sóng đều tăng.
B. tốc độ truyền sóng và bước sóng đều giảm.
C. tốc độ truyền sóng giảm, bước sóng tăng.
D. tốc độ truyền sóng tăng, bước sóng giảm.
Phương pháp giải
Sử dụng lí thuyết về sóng điện điện từ
Hướng dẫn giải
- Sóng điện từ khi truyền từ không khí vào nước thì tốc độ giảm, bước sóng giảm
- Chọn B
9. Giải bài IV.9 trang 63 SBT Vật lý 12
Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do, điện tích của một bản tụ điện và cường độ dòng điện qua cuộn cảm biến thiên điều hòa theo thời gian
A. cùng với tần số.
B. với cùng biên độ.
C. luôn cùng pha nhau.
D. luôn ngược pha nhau.
Phương pháp giải
Trong dao động điện từ điện tích của một bản tụ điện và cường độ dòng điện có cùng tần số
Hướng dẫn giải
- Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do, điện tích của một bản tụ điện và cường độ dòng điện qua cuộn cảm biến thiên điều hòa theo thời gian cùng tần số và vuông pha với nhau
- Chọn A
10. Giải bài IV.10 trang 63 SBT Vật lý 12
Phát biểu nào sau đây là sai khi nói về sóng điện từ?
A. Trong sóng điện từ thì dao động của điện trường và của từ trường tại một điểm luôn đồng pha với nhau.
B. Sóng điện từ là sóng ngang nên nó chỉ truyền đc trong chất rắn.
C. Khi sóng điện từ gặp mặt phân cách giữa hai môi trường thì nó có thể bị phản xạ và khúc xạ.
D. Sóng điện từ truyền được trong chân không.
Phương pháp giải
Để trả lời câu hỏi này cần nắm được các tính chất và đặc điểm của sóng điện từ
Hướng dẫn giải
- B sai vì: Sóng điện từ truyền được trong các môi trường rắn, lỏng, khí và chân không.
- Chọn B
11. Giải bài IV.11 trang 63 SBT Vật lý 12
Một mạch dao động điện từ lí tưởng gồm một cuộn cảm thuần có độ tự cảm 5μH và một tụ điện có điện dung 5μF. Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là bao nhiêu?
Phương pháp giải
- Tính chu kì dao động theo công thức:
\(T = 2\pi \sqrt {LC} \)
- Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là T/2
Hướng dẫn giải
- Ta có chu kì:
\(\begin{array}{l} T = 2\pi \sqrt {LC} \\ = 2\pi \sqrt {{{5.10}^{ - 6}}{{.5.10}^{ - 6}}} = 10\pi {.10^{ - 6}}(s) \end{array}\)
- Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là:
\(t = \frac{T}{2} = \frac{{10\pi {{.10}^{ - 6}}}}{2} = 5\pi {.10^{ - 6}}(s)\)
12. Giải bài IV.12 trang 63 SBT Vật lý 12
Một mạch dao động lí tưởng gồm cuộn cảm thuần có độ tự cảm L không đổi và tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung của tụ điện đến giá trị C1 thì tần số dao động riêng của mạch là f1. Để tần số riêng của mạch là √5f1 thì phải điều chỉnh điện dung của tụ điện đến giá trị nào?
Phương pháp giải
Sử dụng công thức tính tần số:
\(f = \frac{1}{{2\pi \sqrt {LC} }}\) suy ra tỉ lệ giữa C và f
Hướng dẫn giải
- Ta có tần số:
\(f = \frac{1}{{2\pi \sqrt {LC} }} \Rightarrow C \sim \frac{1}{{{f^2}}}\)
- Vậy:
\(\frac{{{C_1}}}{{{C_2}}} = \frac{{f_2^1}}{{f_1^2}} = 5 \Rightarrow {C_2} = \frac{{{C_1}}}{5}\)
13. Giải bài IV.13 trang 63 SBT Vật lý 12
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm 50mH và tụ điện có điện dung C. Trong mạch đang có dao động điện từ tự do với cường độ dòng điện i=0,12cos20000t (i tính bằng A, t tính bằng s). Ở thời điểm mà cường độ dòng điện trong mạch bằng một nửa cường độ hiệu dụng thì hiệu điện thế giữa hai bản tụ có độ lớn bằng bao nhiêu?
Phương pháp giải
- Tính điện dung C theo công thức:
\(\omega = \frac{1}{{\sqrt {LC} }} \Rightarrow {C = \frac{1}{{L{\omega ^2}}}} \)
- Dùng công thức:
\({I_0} = {q_0}\omega \Rightarrow {q_0}={I_0}/{q_0}\) để tính điện tích
- Dùng công thức:
\({q_0} = C{U_0} \Rightarrow {U_0}={q_0}/C\) để tính hiệu điện thế
- Dùng công thức độc lập với thời gian giữa u;i:
\({\left( {\frac{u}{{{U_0}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1\) để tính u
Hướng dẫn giải
- Điện dung là:
\(\begin{array}{l} \omega = \frac{1}{{\sqrt {LC} }}\\ \Rightarrow C = \frac{1}{{L{\omega ^2}}} = \frac{1}{{{{50.10}^{ - 3}}{{.2000}^2}}} = {5.10^{ - 6}}(F) \end{array}\)
-Ta có:
\(\begin{array}{l} + \,{I_0} = {q_0}\omega \\ \Rightarrow {q_0} = \frac{{{I_0}}}{\omega } = \frac{{0,12}}{{2000}} = {6.10^{ - 5}}(C)\\ + \,{q_0} = C{U_0}\\ \Rightarrow {U_0} = \frac{{{q_0}}}{C} = \frac{{{{6.10}^{ - 5}}}}{{{{5.10}^{ - 6}}}} = 12(V) \end{array}\)
- Công thức độc lập với thời gian giữa u;i:
\(\begin{array}{l} + \,{\left( {\frac{u}{{{U_0}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1\\ + \,i = \frac{I}{2} = \frac{{{I_0}}}{{2\sqrt 2 }}\\ \begin{array}{*{20}{l}} { \Rightarrow {{\left( {\frac{u}{{12}}} \right)}^2} + {{\left( {\frac{1}{{2\sqrt 2 }}} \right)}^2} = 1}\\ { \Rightarrow |u| = 3\sqrt {14} (V)} \end{array} \end{array}\)
Tham khảo thêm
- doc Giải bài tập SBT Vật Lí 12 Bài 20: Mạch dao động
- doc Giải bài tập SBT Vật Lí 12 Bài 21: Điện từ trường
- doc Giải bài tập SBT Vật Lí 12 Bài 22: Sóng điện từ
- doc Giải bài tập SBT Vật Lí 12 Bài 23: Nguyên tắc thông tin liên lạc bằng sóng vô tuyến



