Giải bài tập SBT Vật Lí 12 Bài tập cuối chương 2 - Sóng cơ và sóng âm

Bước sóng là khoảng cách giữa hai điểm

A. gần nhau nhất mà dao động tại hai điểm đó cùng pha.

B. trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.

C. trên cùng một phương truyền sóng mà dao động tại hai điểm đó ngược pha.

D. gần nhau nhất trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.

Phương pháp giải

Để trả lời câu hỏi này cần nắm được định nghĩa của bước sóng

Hướng dẫn giải

- Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.

- Chọn D

Một sóng cơ có tần số 0,5Hz truyền trên một sợi dây đàn hồi đủ dài với tốc độ 0,5m/s. Sóng này có bước sóng là

A. 1,2m                            B. 1,0m

C. 0,8m                            D. 0,5m

Phương pháp giải

Công thức tính bước sóng: λ = v/f

Hướng dẫn giải

- Bước sóng: λ = v/f = 0,5/ 0,5 = 1 (m)

- Chọn B

Một sóng cơ truyền dọc theo trục Ox có phương trình là u = 0,05cos(6πt−πx) (m;s). Tốc độ truyền sóng này là

A. 30m/s.                        B. 3m/s.

C. 6m/s.                          D. 60m/s.

Phương pháp giải

- Từ phương trình sóng ⇒ tìm λ

- Áp dụng công thức tính tốc độ truyền sóng:

v = λ.f

Hướng dẫn giải

- Phương trình sóng tại điểm cách nguồn đoạn x là:

 u = Acos(ωt−2πx/λ)

- Từ phương trình sóng 

⇒ 2πx/λ = πx ⇒ λ = 2m

- Tần số: f = ω/2π  =6π/2π = 3Hz

- Tốc độ truyền sóng: v = λf = 2.3 = 6 (m/s)

- Chọn C

Một sóng ngang truyền theo chiều dương của trục Ox, có phương trình là u=6cos(4πt−0,02πx)(cm;s). Sóng này có bước sóng là

A. 200cm.                      B. 100cm

C. 150cm.                      D. 50cm.

Phương pháp giải

Vận dụng công thức tính độ lệch pha: 2πx/λ để tìm λ

Hướng dẫn giải

- Phương trình sóng tại điểm cách nguồn đoạn x là:

 u = Acos(ωt−2πx/λ)

- Từ phương trình sóng 

⇒ 2πx/λ = 0,02πx ⇒ λ = 100cm

- Chọn B

Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số 120Hz, tạo ra sóng ổn định trên mặt chất lỏng. Xét 5 gợn lồi liên tiếp trên một phương truyền sóng, ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm 0,5m.Tốc độ truyền sóng là

A. 30m/s.                     B. 25m/s.

C. 12m/s.                     D. 15m/s.

Phương pháp giải

- Khoảng cách từ gợn lồi thứ nhất đến gợn thứ năm là 4λ

- Áp dụng công thức v = λf để tính tốc độ truyền sóng 

Hướng dẫn giải

- Khoảng cách hai gợn lồi liên tiếp là λ

- Khoảng cách từ gợn thứ nhất đến gợn thứ năm là 4λ

⇒ 4λ =0,5 ⇒ λ = 0,125m

- Tốc độ truyền sóng v = λf = 0,125.120 = 15(m/s)

- Chọn D

Trên một dây đàn hồi dài 1,8m, hai đầu cố định, đang có sóng dừng với 6 bụng sóng. Biết sóng truyền trên dây có tần số 100Hz. Tốc độ truyền sóng trên dây là

A. 20m/s.                        B. 600m/s.

C. 60m/s.                        D. 10m/s.

Phương pháp giải

- Sử dụng điều kiện sóng dừng: 

 l = kλ/2

- Công thức tính tốc độ truyền sóng: v = λf

Hướng dẫn giải

- Điều kiện sóng dừng trên dây với hai đầu cố định: 

l = kλ/2

- Trên dây có 6 bụng sóng ⇒k=6

λ = 2l/k = 2.1,8/6 = 0,6m

- Tốc độ truyền sóng: v = λ.f = 0,6.100 = 60(m/s)

- Chọn C

Tại một vị trí trong môi trường truyền âm, một sóng âm có cường độ âm I. Biết cường độ âm chuẩn là I₀. Mức cường độ âm L của sóng âm này tại vị trí đó được tính bằng công thức:

A. L(dB) = 10.lg (I/I₀).

B. L(dB) = 10.lg (I₀/I).

C. L(dB) = lg (I₀/I).

D. L(dB) = lg (I/I₀).

Phương pháp giải

Dựa vào công thức tính mức cường độ âm:

L(dB) = 10log(I/I₀).

Hướng dẫn giải

- Mức cường độ âm:

L(dB) = 10log(I/I₀).

- Trong đó:

+ I là cường độ âm tại vị trí xét

+ I₀ là cường độ âm chuẩn

- Chọn A.

Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 50Hz, được đặt tại hai điểm S₁ và S₂ cách nhau 10cm. Tốc độ truyền sóng trên mặt nước là 75cm/s. Xét các điểm trên mặt nước thuộc đường tròn tâm S₁, bán kính S₁S₂, điểm mà phân tử tại đó dao động với biên độ cực đại cách điểm S₂ một đoạn ngắn nhất bằng

A. 8,9m.                           B. 1,5m.

C. 8,5cm.                         D. 1,0cm.

Phương pháp giải

- Dựa vào điều kiện cực đại giao thoa:

 d₂−d₁=kλ

- Xét trong khoảng: −S₁S₂ < kλ < S₁S₂

⇒ tìm k = -6 là phù hợp yêu cầu

⇒ MS₂ − MS₁ = −6λ

Hướng dẫn giải

- Bước sóng: λ = v/f =75/50 = 1,5cm

- Xét:−S₁S₂ < kλ < S₁S₂

⇔ −10 < k.1,5 < 10

⇔ −6,6 < k < 6,6

⇒ k = −3;.....;3

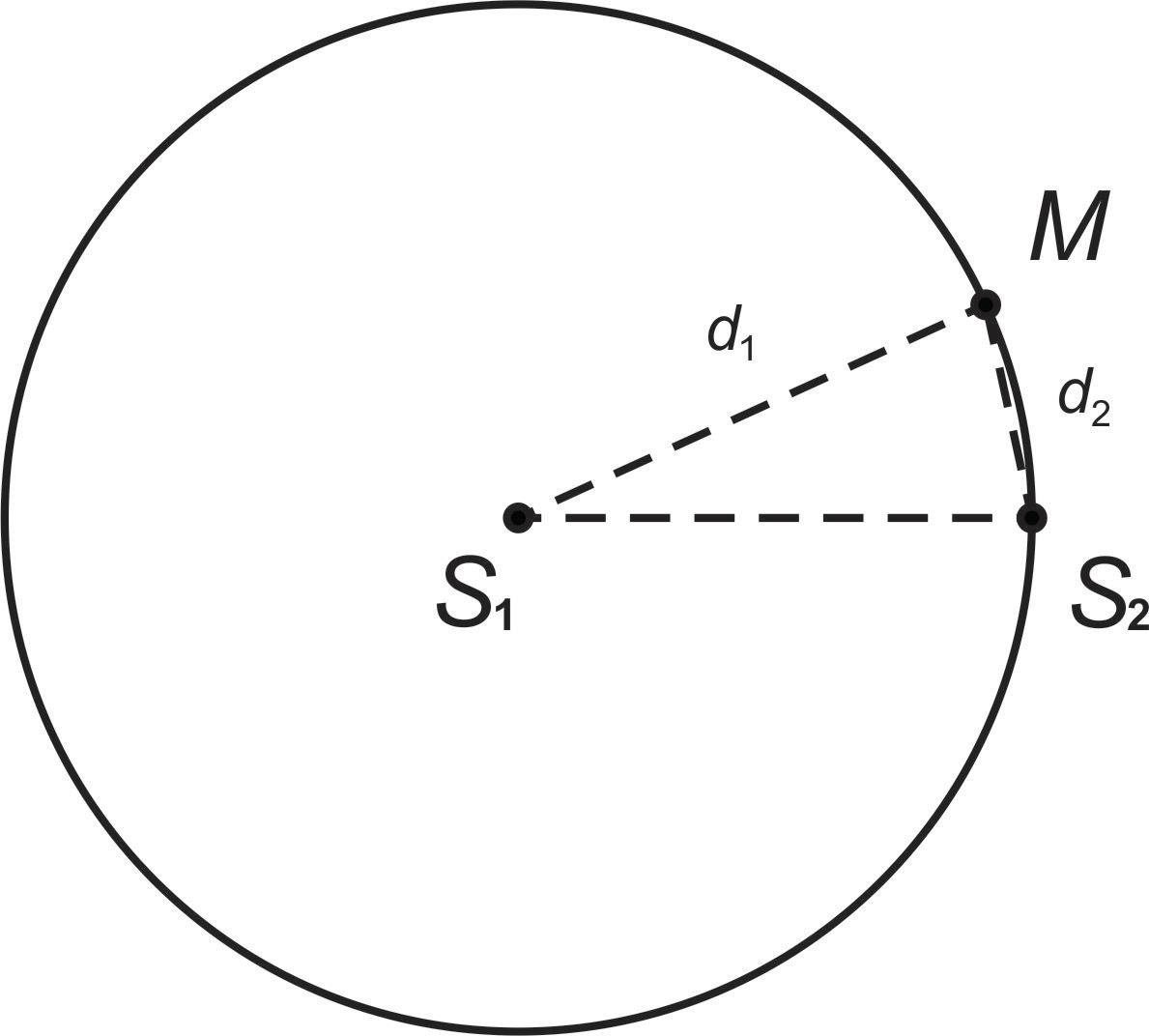
- Do M là điểm mà phân tử tại đó dao động với biên độ cực đại cách điểm S₂ một đoạn ngắn nhất nên M thuộc đường cực đại k=−6

⇒ MS₂ − MS₁ = −6λ = −6.1,5 =−9

MS₁ = S₁S₂ = 10cm ⇒ MS₂ = 1cm

- Chọn D

Hai điểm M,N cùng nằm trên một hướng truyền sóng và cách nhau một phần ba bước sóng. Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm khi li độ dao động của phần tử tại M là 3cm thì li độ dao động của phần tử tại N là −3cm. Biên độ của sóng bằng

A. 2√3cm.                      B. 3√2cm.

C. 3m.                            D. 6cm.

Phương pháp giải

-  Tính độ lệch pha theo công thức

\({\rm{\Delta }}\varphi = \frac{{2\pi d}}{\lambda } \)

- Sử dụng vòng tròn lượng giác để tìm α

⇒ biên độ A từ công thức:

\(\begin{array}{l} {x_M} = A\cos ( - \frac{\pi }{6})\\ \end{array}\)

Hướng dẫn giải

- Ta có: độ lệch pha giữa M và N là:

\({\rm{\Delta }}\varphi = \frac{{2\pi d}}{\lambda } = \frac{{2\pi .\frac{\lambda }{3}}}{\lambda } = \frac{{2\pi }}{3}rad\)

- Ta có vòng tròn lượng giác:

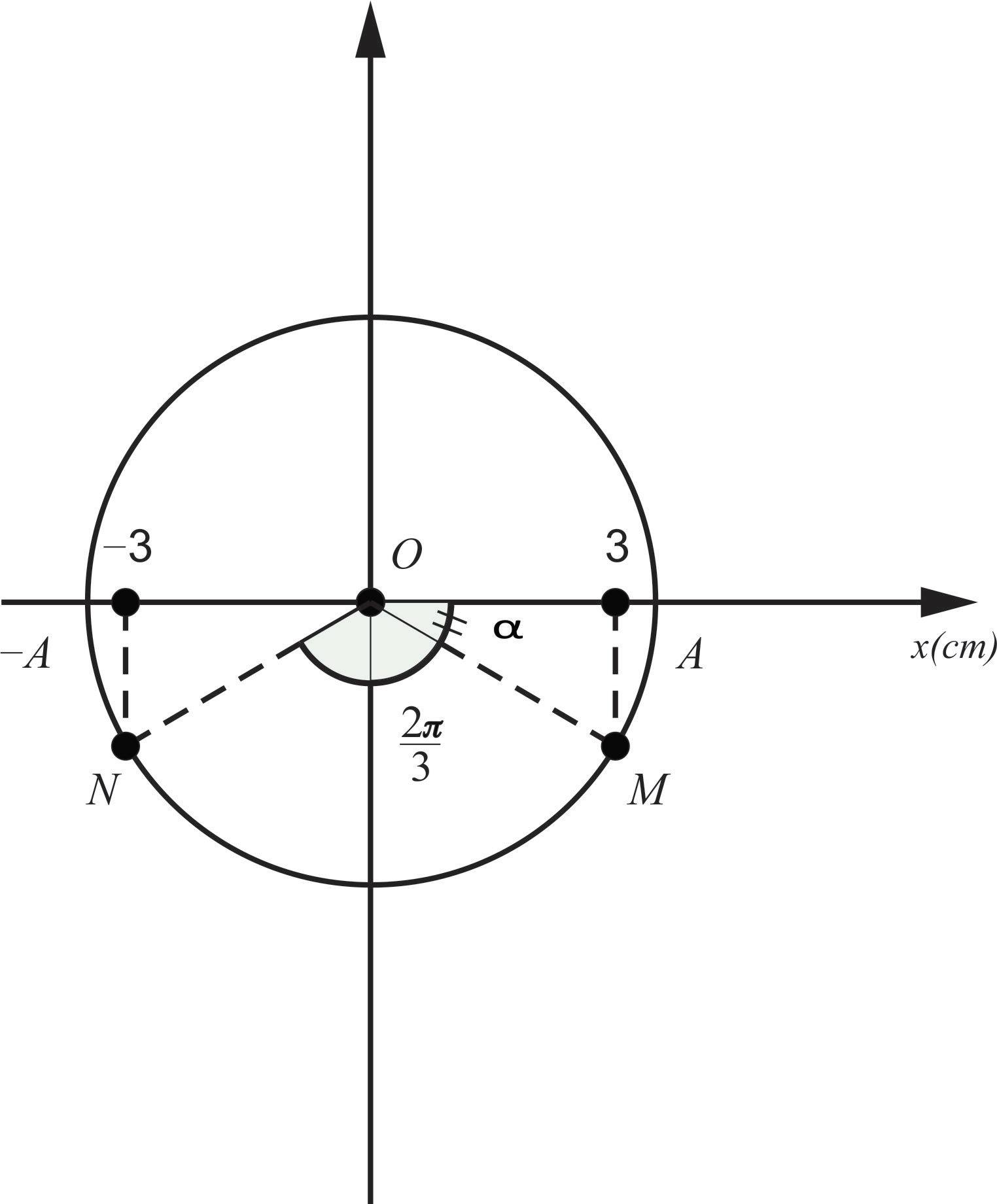
- Từ hình vẽ: suy ra α = −π/6 rad

\(\begin{array}{l} {x_M} = A\cos ( - \frac{\pi }{6})\\ \Rightarrow A = \frac{{{x_M}}}{{\cos ( - \frac{\pi }{6})}} = \frac{3}{{\cos ( - \frac{\pi }{6})}} = 2\sqrt 3 cm \end{array}\)

- Chọn A

Trên một sợi dây đàn hồi dài 100cm với hai đầu A và B cố định đang có sóng dừng, tần số sóng là 50Hz. Không kể hai đầu A và B, trên dây có 3 nút sóng. Tốc độ truyền sóng trên dây là

A. 30m/s.                        B. 20m/s.

C. 25m/s.                        D. 15m/s.

Phương pháp giải

- Vận dụng điều kiện sóng dừng:

l = kλ/2

- Công thức tính tốc độ truyền sóng:

v = λ.f

Hướng dẫn giải

- Tổng số nút trên dây là 5⇒ k=4

- Điều kiện sóng dừng trên dây với hai đầu cố định: 

l = kλ/2 ⇒ λ = 2l/k = 2.100/4 = 50cm

- Tốc độ truyền sóng:

v = λ.f = 50.50 = 2500cm/s = 25m/s

- Chọn C

Một sóng ngang truyền theo chiều dương của trục x trên một dây đàn hồi dài. Tại thời điểm xét, dây có dạng như hình II.1. Xét hai điểm P và Q của dây. Hướng chuyển động của hai điểm đó lần lượt là:

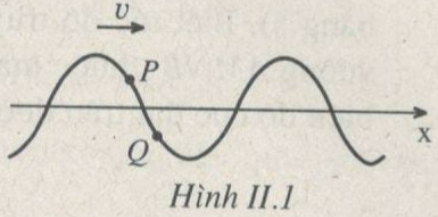
A. đi xuống; đi xuống.

B. đi xuống; đi lên.

C. đi lên; đi xuống.

D. đi lên; đi lên.

Phương pháp giải

Dùng đồ thị sóng hình sin

Hướng dẫn giải

Sóng truyền từ trái sang phải

- Dạng sóng trên dây tại thời điểm t (nét liền) và thời điểm t+dt (nét đứt)

-Ta có đồ thị:

- Từ đồ thị ta thấy, cả P và Q đều dịch chuyển đi lên

- Chọn D

Trên một sợi dây căng ngang với hai đầu cố định đang có sóng dừng. Không kể các điểm nút hoặc bụng, người ta còn thấy có những điểm cách đều nhau và dao động với cùng biên độ. Nếu khoảng cách ngắn nhất giữa chúng là 15cm thì bước sóng của sóng truyền trên dây bằng

A. 90cm.                           B. 60cm.

C. 45cm.                           D. 30cm.

Phương pháp giải

Sử dụng công thức tính biên độ tại điểm cách nút gần nhất đoạn là d: 

A_M = 2Asin(2πd/λ)

Hướng dẫn giải

- Biên độ tại điểm cách nút gần nhất đoạn là d: A_M = 2Asin2πd/λ

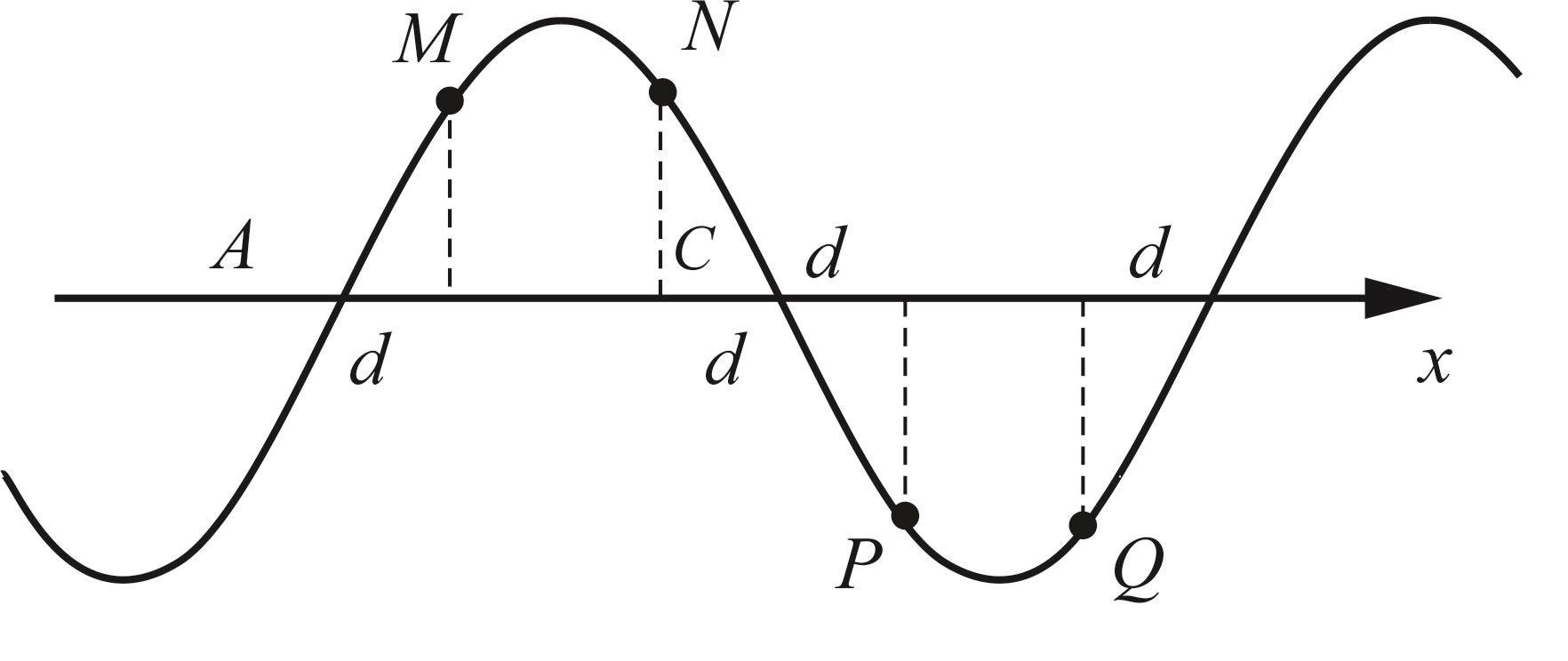
- Gọi M, N, P, Q là các điểm có cùng biên độ và cách đều nhau, chúng cùng cách nút các đoạn bằng d

MN = PQ = λ/2 − 2d; NP = 2d

- Theo đề:

 MN = NP = PQ = 15cm

⇒ d = 7,5cm; λ = 60cm

- Chọn B

Cường độ âm tại một điểm trong môi trường truyền âm là 10⁻⁴W/m². Biết cường độ âm chuẩn là 10⁻¹²W/m². Mức cường độ âm tại điểm đó bằng

A. 80dB.                         B. 8dB.

C. 0,8dB.                        D. 80B.

Phương pháp giải

Sử dụng công thức tính mức cường độ âm tại một điểm: 

L = 10log(I/I₀) 

Hướng dẫn giải

- Mức cường độ âm tại một điểm: 

L = 10log(I/I₀) = 10log(10⁻⁴/10⁻¹²) = 80 (dB)

- Chọn A

Một sợi dây dài 100cm căng ngang, đầu B cố định, đầu A gắn với một nhánh của âm thoa dao động điều hòa với tần số 40Hz. Trên dây AB có sóng dừng ổn định, A được coi là nút sóng. Tốc độ truyền sóng trên dây là 20m/s. Hỏi kế cả A và B, trên dây có bao nhiêu bụng và bao nhiêu nút?

Phương pháp giải

- Điều kiện sóng dừng trên dây với hai đầu cố định:

l = kλ/2 (k nguyên)

- k = số bụng = số nút-1

Hướng dẫn giải

- Bước sóng: λ = v/f = 20/40 = 0,5m = 50cm

- Điều kiện sóng dừng trên dây với hai đầu cố định:

 l = kλ/2 ⇒ k = 2l/λ= 2.100/50 = 4

Vậy trên dây có 4 bụng và 5 nút

Ở mặt chất lỏng có hai nguồn A,B cách nhau 18cm, dao động theo phương thẳng đứng với phương trình là u_A=u_B=acos50πt. Tốc độ truyền sóng ở mặt chất lỏng là 50cm/s. Gọi O là trung điểm của AB, điểm M ở mặt chất lỏng nằm trên đường trung trực của AB và gần O nhất sao cho phần tử chất lỏng tại M dao động cùng pha với phần tử chất lỏng tại O. Hỏi khoảng cách là bao nhiêu?

Phương pháp giải

- Tính tần số theo công thức: f = ω/2π

- Bước sóng được tính theo công thức: λ = v/f

- Điều kiện cùng pha: d = kλ

- Từ hình vẽ 

⇒ để cùng pha O thì M cùng pha với M′

⇒ từ MM' = λ tìm OM

Hướng dẫn giải

- Tần số: f = ω/2π = 50π/2π = 25Hz

- Bước sóng: λ = v/f = 50/25 = 2cm

- Độ lệch pha giữa nguồn và điểm cách nguồn một đoạn d là Δφ = 2πd/λ, vậy tất cả các điểm thuộc đường tròn tâm A bán kính AO đều cùng pha với O

⇒M′ cùng pha với O

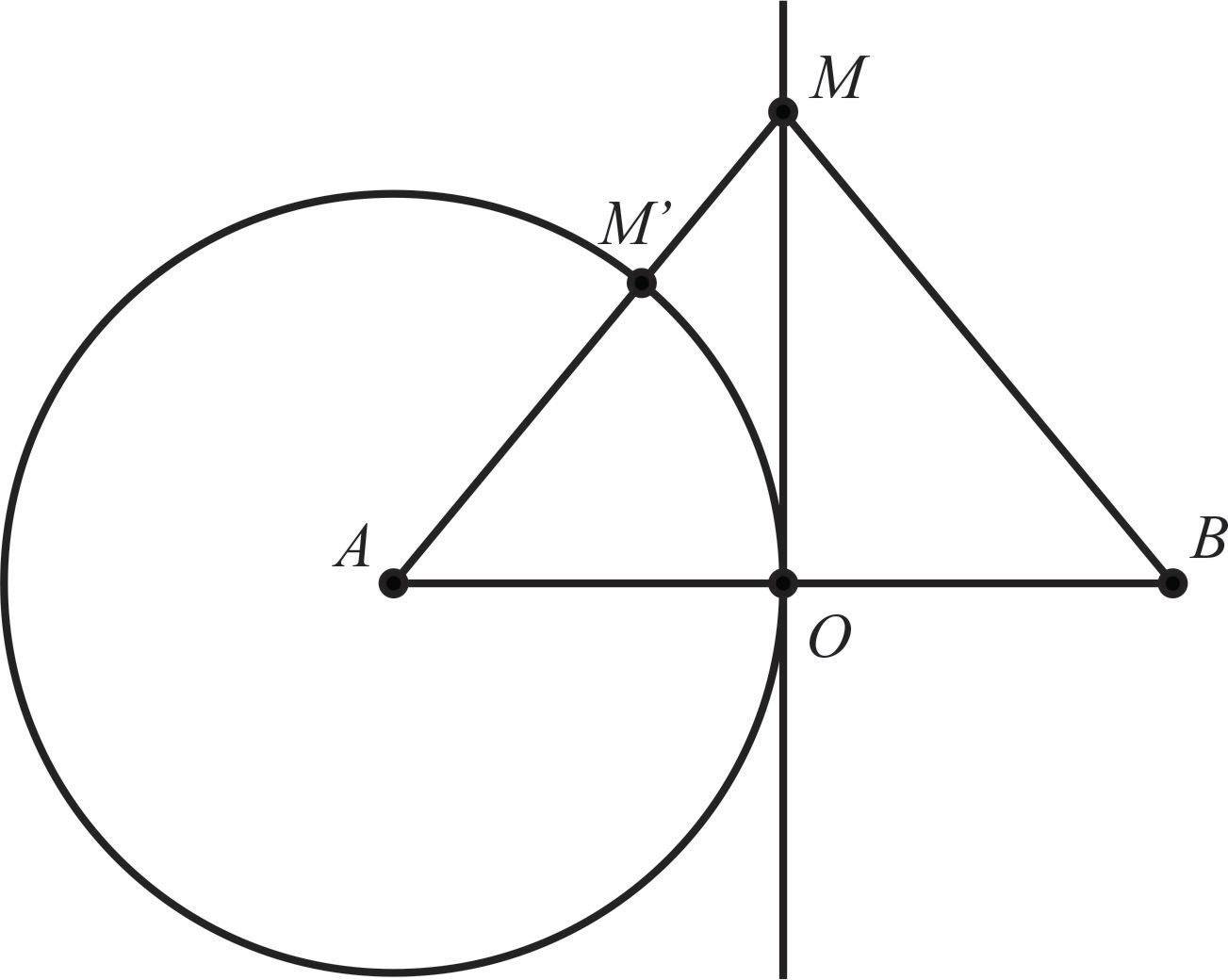
- Để M là điểm gần O nhất, cùng pha với O thì M cùng pha với M′, gần M′ nhất 

\(\begin{array}{l} \Rightarrow MM' = \lambda \\ \Rightarrow AM = AO + \lambda \\ \begin{array}{*{20}{l}} {OM = \sqrt {A{M^2} - A{O^2}} }\\ { = \sqrt {{{(AO + \lambda )}^2} - A{O^2}} }\\ { = \sqrt {{{(9 + 2)}^2} - {9^2}} = 2\sqrt {10} cm} \end{array} \end{array}\)

Hai sóng mặt nước phát ra từ hai nguồn S₁,S₂ dao động cùng pha (Hình II.2). M là một điểm nằm trên đường cực tiểu giao thoa thứ hai. Hiệu đường đi MS₁−MS₂=4,5cm. Hỏi bước sóng bằng bao nhiêu?

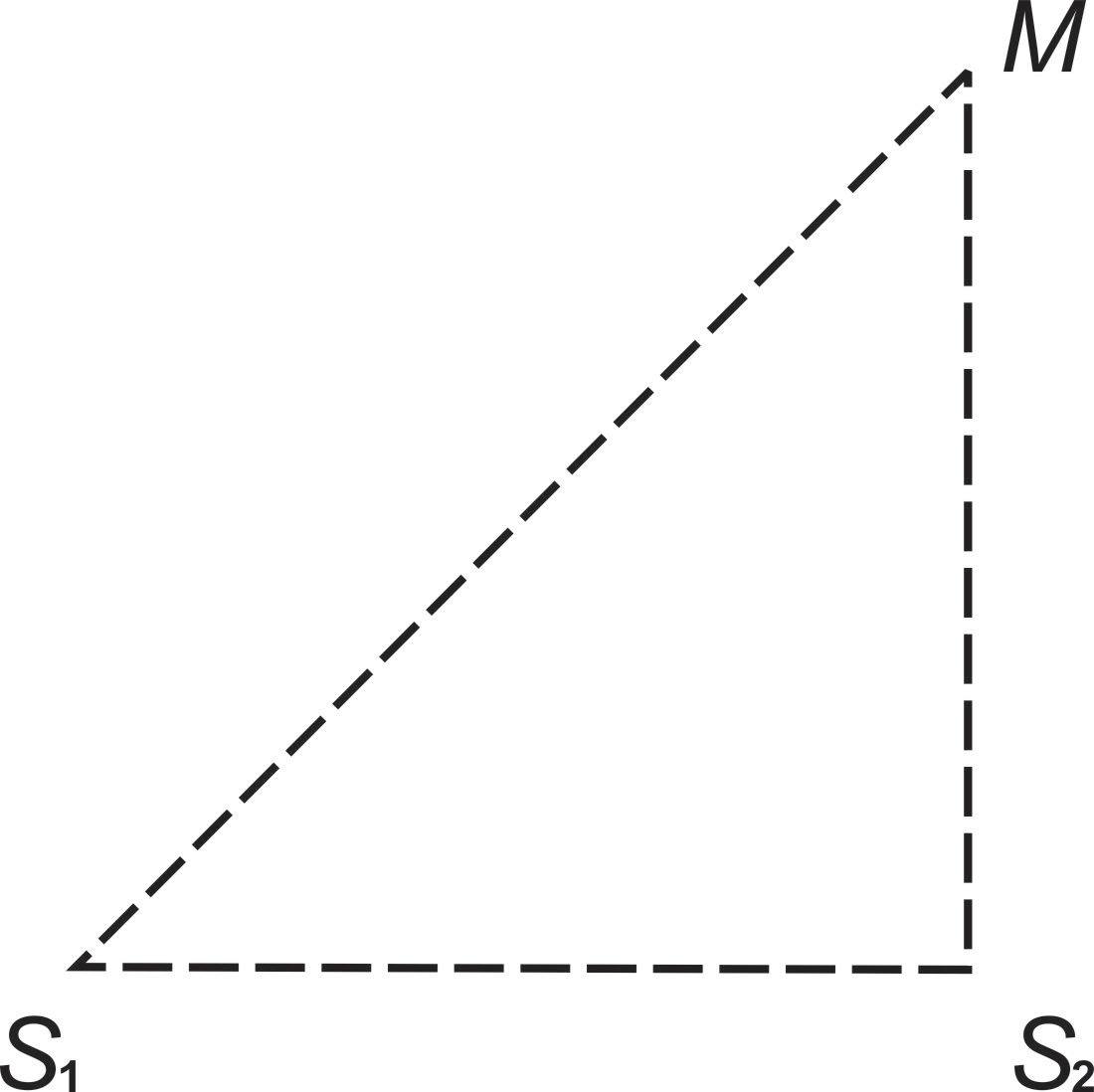
Phương pháp giải

Dựa vào điều kiện cực tiểu giao thoa:

d₂−d₁=(k+1/2)λ để tính bước sóng

Hướng dẫn giải

- Điều kiện biên độ cực tiểu hai nguồn cùng pha:

d₂−d₁=(k+1/2)λ

- Vì M thuộc đường cực tiểu giao thoa thứ hai ⇒k=2

⇒ M_S1 − M_S2 = 4,5cm = (2+1/2)λ ⇒ λ = 1,8cm

Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 20cm, dao động theo phương thẳng đứng với phương trình U_A=2cos40πt và U_B=2cos(40πt+π) (U_A và U_B tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt chất lỏng là 30cm/s. Xét hình vuông AMNB thuộc mặt thoáng của chất lỏng. Hỏi số điểm dao động với biên độ cực đại trên đường chéo BM của hình vuông là bao nhiêu?

Phương pháp giải

- Tính tần số và bước sóng theo công thức:

f = ω/2π và λ = v/f

- Áp dụng điều kiện biên độ cực tiểu hai nguồn cùng pha:

d₂−d₁ = kλ

- Xét trong đoạn:

d_2B − d_1B < kλ ≤ d_2M − d_1M

⇒ có 19 giá trị k thỏa mãn

Hướng dẫn giải

- Tần số: f = ω/2π = 40π/2π = 20Hz

- Bước sóng: λ = v/f = 30/20 = 1,5cm

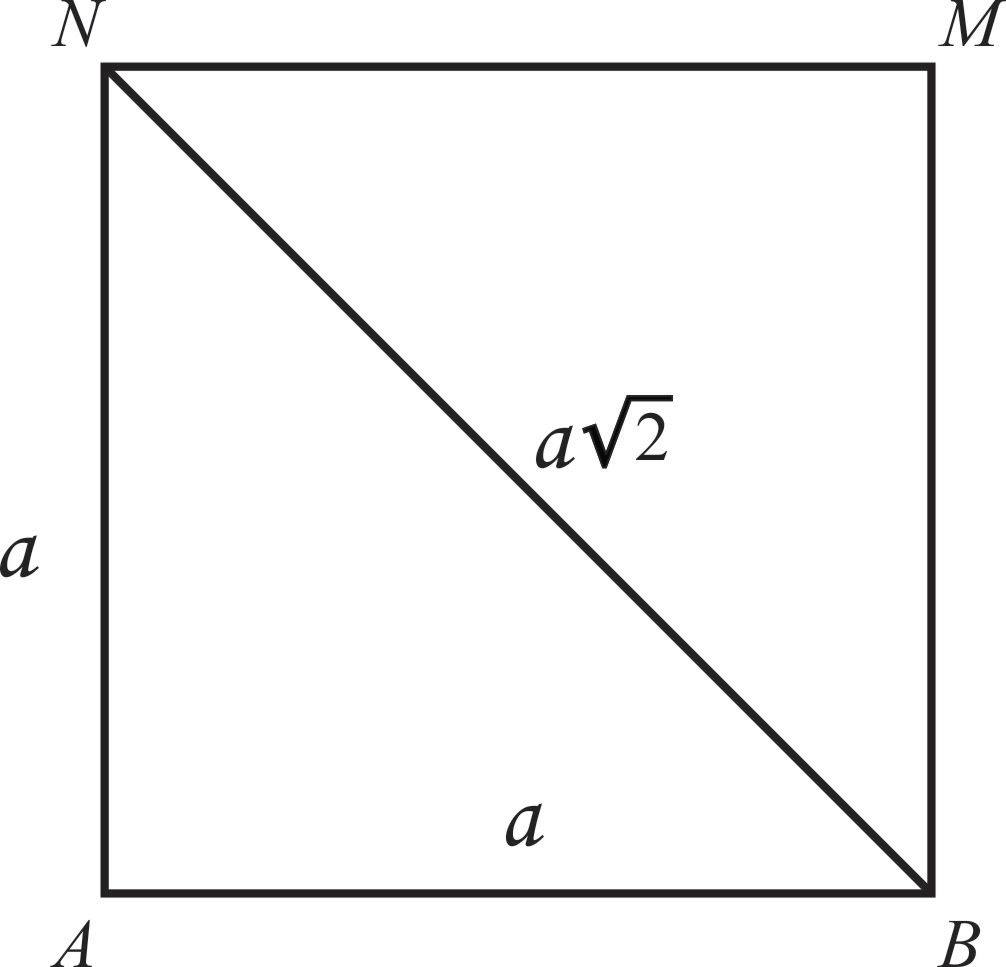
- Tại M: 

+ d_1M = AM = 20cm

+ d_2M = MB = 20√2cm

- Tại B:

+ d_1B = AB = 20cm

+ d_2B = BB = 0

- Điều kiện biên độ cực đại hai nguồn cùng pha:

d₂−d₁= kλ

⇒ d_2B − d_1B < kλ ≤ d_2M − d_1M

(Vì B không thể là cực đại nên không lấy dấu bằng)

⇔ 0−20 < k.1,5 ≤ 20√2−20

⇔ −13,4 < k ≤ 5,5 

⇒ k = −13;....;5

Vậy có 19 giá trị k nguyên tương ứng với 19 cực đại trên BM