Giải bài tập SBT Vật Lí 12 Bài 8: Giao thoa sóng

Hai nguồn phát sóng nào dưới đây chắc chắn là hai nguồn kết hợp?  Hai nguồn có

A. cùng tần số.

B. cùng biên độ dao động.

C. cùng pha ban đầu.

D. cùng tần số và hiệu số pha không đổi theo thời gian.

Phương pháp giải

Để trả lời câu hỏi này cần nắm được định nghĩa hai nguồn sóng kết hợp

Hướng dẫn giải

- Hai nguồn kết hợp có cùng phương, cùng tần số và hiệu số pha không đổi theo thời gian.

- Chọn D

Hai sóng phát ra từ hai nguồn đồng bộ. Cực đại giao thoa nằm tại các điểm có hiệu khoảng cách tới hai nguồn bằng

A. Một bội số của bước sóng.

B. Một ước số nguyên của bước sóng.

C. Một bội số lẻ của nửa bước sóng.

D. Một ước số của nửa bước sóng.

Phương pháp giải

Áp dụng điều kiện cực đại giao thoa:

 d₂−d₁ = kλ 

Hướng dẫn giải

- Cực đại giao thoa nằm tại các điểm có hiệu khoảng cách tới hai nguồn bằng một bội số của bước sóng.

- Chọn A

Hai nguồn phát sóng đồng bộ S₁,S₂ nằm sâu trong một bể nước. M và N là điểm trong bể nước có hiệu khoảng cách tới S₁ và S₂ bằng một số bán nguyên lần bước sóng. M nằm trên đường thẳng S₁S₂; N nằm ngoài đường thẳng đó (H.8.1 ).

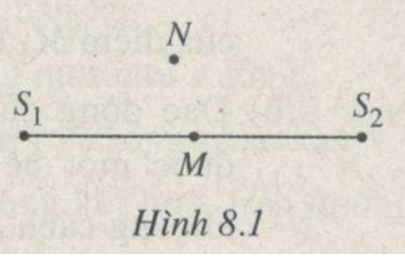
Chọn phát biểu đúng:

A. Các phần tử nước ở M và N đều đứng yên.

B. Các phần tử nước ở M và N đều dao động.

C. Các phần tử nước ở M dao động, ở N đứng yên.

D. Các phần tử nước ở M đứng yên, ở N dao động.

Phương pháp giải

Sử dụng điều kiện giao thoa sóng hai nguồn cùng pha: 

+ cực đại: d₂−d₁ = kλ

+ cực tiểu: d₂−d₁= (k+1/2)λ

Hướng dẫn giải

- M và N là điểm trong bể nước có hiệu khoảng cách tới S1 và S2 bằng một số bán nguyên lần bước sóng, thỏa mãn điều kiện cực tiểu

⇒ Các phần tử nước tại M và N đều đứng yên

- Chọn A

Ở mặt nước có hai nguồn kết hợp A,B dao động theo phương thẳng đứng với phương trình u_A=u_B=2cos20πt(mm). Tốc độ truyền sóng là 30cm/s. Coi biên độ sóng không đổi khi sóng truyền đi. Phần tử M ở mặt nước cách hai nguồn lần lượt là 10,5cm và 13,5cm có biên độ dao động là

A. 1mm                          B. 0mm

C. 2mm                          D. 4mm

Phương pháp giải

- Tính tần số và bước sóng theo công thức:

f = ω/2π và λ = v/f

- Vận dụng điều kiện giao thoa sóng:

+ cực đại: d₂−d₁ = kλ

+ cực tiểu: d₂−d₁ = (k+1/2)λ

Hướng dẫn giải

Ta có:

d_2M = 13,5cm

d_1M = 10,5cm

- Tần số:

f = ω/2π = 20π/2π = 10Hz

- Bước sóng là:

λ = v/f = 30/10 = 3cm

Ta có:

d_2M − d_1M = 13,5 − 10,5 = 3cm = 1.λ

⇒ tại M là một cực đại 

⇒ AM = 2a = 2.2 = 4cm

Hai nguồn sóng S₁,S₂ trên mặt chất lỏng, cách nhau 18cm, dao động cùng pha với tần số 20Hz. Tốc độ sóng là 1,2m/s. Số điểm trên đoạn S₁S₂ dao động với biên độ cực đại là

A. 5                                   B. 4

C. 3                                   D. 2

Phương pháp giải

- Áp dụng công thức: λ = v/f để tính bước sóng

- Sử dụng điều kiện cực đại giao:

d₂−d₁= kλ

- Xét: −S₁S₂ < kλ < S₁S₂

⇒ Số giá trị k nguyên là số điểm dao động biên độ cực đại trên S₁S₂

Hướng dẫn giải

- Bước sóng là:

λ = v/f = 1,2/20 = 0,06 m = 6cm

Xét: −S₁S₂ < kλ < S₁S₂

⇔ −18 < k.6 < 18

⇔ −3 < k <3

⇒k=−2;.....;2

⇒ Có 5 giá trị kk nguyên 

⇒ Có 5 cực đại trên đoạn  S₁S₂

- Chọn A

Ở bề mặt một chất lỏng có hai nguồn kết hợp  S₁S₂ và  S₁,S₂ cách nhau 20cm. Hai nguồn này dao động theo phương thẳng đứng có phương trình lần lượt là u₁=5cos40πt(mm) và u₂=5cos(40πt+π)(mm). Tốc độ truyền sóng trên mặt chất lỏng là 80cm/s. Số điểm dao động với biên độ cực tiểu trên đoạn thẳng S₁S₂ là

A. 11                                    B. 9

C. 10                                   D. 8

Phương pháp giải

- Tính tần số và bước sóng theo công thức:

f = ω/2π và λ = v/f

- Áp dụng công thức:

d₂−d₁= (k+1/2)λ để tính hiệu đường đi của hai cực tiểu

- Xét: −S₁S₂ < (k+1/2)λ < S₁S₂

⇒ Số giá trị k nguyên là số điểm dao động biên độ cực tiểu trên S₁S₂

Hướng dẫn giải

- Tần số:

f = ω/2π = 40π/2π = 20Hz

- Bước sóng:

λ = v/f = 80/20 = 4cm

Xét: −S₁S₂ < (k+1/2)λ < S₁S₂

⇔ −20 < (k+1/2).4 < 20

⇔ −5,5 < k < 4,5

⇒k = −5;.....;4

⇒ Có 10 giá trị k nguyên

 ⇒ Có 10 cực tiểu trên đoạn S₁S₂

- Chọn C

Hai điểm S₁,S₂ trên mặt một chất lỏng, cách nhau 18cm, dao động cùng pha với biên độ A và tần số f=20Hz. Tốc độ truyền sóng trên mặt chất lỏng là v=1,2m/s. Hỏi giữa S₁,S₂ có bao nhiêu gợn sóng (cực đại của giao thoa) hình hypebol?

Phương pháp giải

- Tính bước sóng theo công thức: λ = v/f

- Áp dụng công thức:

 d₂−d₁ = kλ tính hiệu đường đi của hai cực đại giao thoa

- Xét: −S₁S₂ < kλ < S₁S₂

⇒ Số giá trị k nguyên là số điểm dao động biên độ cực đại trên S₁S₂

Hướng dẫn giải

- Bước sóng là:

λ = v/f = 1,2/20 = 0,06m =6cm

- Xét: −S₁S₂ < kλ < S₁S₂

⇔−18 < k.6 < 18

⇔−3 < k < 3

⇒ k = −2;.....;2

⇒Có 5 giá trị k nguyên 

⇒ Có 5 cực đại trên đoạn S₁S₂

- Chú ý: Tại nguồn không thể có cực đại

Vậy, nếu không tính gợn thẳng trùng với đường trung trực của S₁S₂ thì có 4 gợn sóng hình hypebol

Hai mũi nhọn S₁,S₂ cách nhau 8cm, gắn ở đầu một cần rung có tần số f = 100Hz được đặt cho chạm nhẹ vào mặt một chất lỏng. Tốc độ truyền sóng trên mặt chất lỏng là v = 0,8m/s.

a) Gõ nhẹ cần rung thì hai điểm S₁,S₂ dao động theo phương thẳng đứng với phương trình dạng u = Acos2πft. Hãy viết phương trình dao động của điểm M₁ trên mặt chất lỏng cách đều S₁,S₂ một khoảng d=8cm.

b) Dao động của cần rung được duy trì bằng một nam châm điện. Để được một hệ vân giao thoa ổn định trên mặt chất lỏng, phải tăng khoảng cách S₁S₂ một đoạn ít nhất bằng bao nhiêu? Với khoảng cách ấy thì giữa hai điểm S₁,S₂ có bao nhiêu gợn sóng hình hypebol?

Phương pháp giải

Tính bước sóng theo công thức: λ = v/f

a) Sử dụng phương trình sóng tổng hợp tại điểm cách nguồn S₁ đoạn d₁ và cách nguồn S₂ đoạn d₂: 

\(u = 2A\cos \frac{{\pi ({d_2} - {d_1})}}{\lambda }cos(2\pi ft - \frac{{\pi ({d_2} + {d_1})}}{\lambda })\)

b)  Trung điểm I là cực đại giao thoa

⇒  S₁S₂  = 10λ ⇒ số gợn sóng

Hướng dẫn giải

- Bước sóng là:

λ = v/f = 0,8/100 = 0,008m = 0,8cm

a) Phương trình sóng tại điểm cách nguồn đoạn d:

\(\begin{array}{*{20}{l}} \begin{array}{l} u = 2A\cos \frac{{\pi ({d_2} - {d_1})}}{\lambda }cos(2\pi ft - \frac{{\pi ({d_2} + {d_1})}}{\lambda })\\ = 2A\cos \frac{{\pi (8 - 8)}}{{0,8}}cos(2\pi .100t - \frac{{\pi .(8 + 8)}}{{0,8}}) \end{array}\\ { = 2Acos(200\pi t - 20\pi )} \end{array}\)

b) Khi hệ vân giao thoa đã ổn định thì trung điểm I của S₁S₂ lại luôn luôn là cực đại giao thoa. 

- Do đó ta phải có:

\(\begin{array}{*{20}{l}} {{S_1}I = {S_2}I = k\frac{\lambda }{2} + \frac{\lambda }{4} = (2k + 1)\frac{\lambda }{4}}\\ {{S_1}{S_2} = 2{S_1}I = (2k + 1)\frac{\lambda }{2}} \end{array}\)

- Ban đầu ta có:

 S₁S₂ = 4cm = 10λ = 20.λ/2

- Vậy chỉ cần tăng khoảng cách S₁S₂ thêm λ/2  

⇒ Khi đó không tính gợn thẳng trùng với đường trung trực của S₁S₂ thì có 20 gợn sóng hình hypebol.

Một người làm thí nghiệm Hình 8.1 SGK với một chất lỏng và một cần rung có tần số 20Hz. Giữa hai điểm S₁,S₂ người đó đếm được 12 đường hypebol, quỹ tích của các điểm đứng yên. Khoảng cách giữa đỉnh của hai đường hypebol ngoài cùng là 22cm. Tính tốc độ truyền sóng.

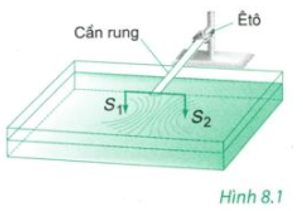
Phương pháp giải

- Sử dụng biểu thức khoảng cách giữa hai đỉnh hypebol (các điểm đứng yên) gần nhau nhất bằng λ/2

- Tốc độ truyền sóng: v=λf

Hướng dẫn giải

- Giữa đỉnh của hypebol thứ nhất đến hypebol thứ 12 có 11 khoảng λ/2

⇒ khoảng cách: 11.λ/2 = 22cm

⇒ λ = 4cm

- Tốc độ truyền sóng v = λf = 4.20 = 80cm/s

Dao động tại hai điểm S₁,S₂ cách nhau 12cm trên một mặt chất lỏng có biểu thức: u=Acos100πt, tốc độ truyền sóng trên mặt chất lỏng là 0,8m/s.

a) Giữa hai điểm có bao nhiêu đường hypebol, tại đó chất lỏng dao động mạnh nhất?

b) Viết biểu thức  của dao động tại điểm M, cách đều S₁,S₂ một khoảng 8cm, và tại điểm M′ nằm trên đường trung trực của S₁S₂ và cách đường S₁S₂ một khoảng 8cm.

Phương pháp giải

a) - Tính tần số và bước sóng theo công thức:

f = ω/2π và  λ = v/ f

- Áp dụng công thức:

d₂−d₁= kλ để tính hiệu đường đi của hai cực đại

Xét: −S₁S₂ < kλ < S₁S₂

Số giá trị k nguyên là số điểm dao động biên độ cực đại trên S₁S₂

b) Sử dụng phương trình sóng tổng hợp tại điểm cách nguồn S₁ đoạn d₁ và cách nguồn S₂ đoạn d₂:

\(u = 2A\cos \frac{{\pi ({d_2} - {d_1})}}{\lambda }cos(2\pi ft - \frac{{\pi ({d_2} + {d_1})}}{\lambda })\)

Hướng dẫn giải

- Tần số: f = ω/2π = 100π/2π = 50Hz

- Bước sóng: λ = v/ f= 0,8/50 = 0,016m = 1,6cm

- Xét: −S₁S₂ < kλ < S₁S₂

⇔−12 < k.1,6 < 12

⇔−7,5 < k < 7,5

⇒ k = −7;.....;7.

Có 15 giá trị của k

- Quỹ tích các điểm dao động với biên độ cực đại là đường hypebol

- Nếu coi đường trung trực của S₁S₂ như một hypebol đặc biệt thì số đường hypebol là 15

b) M cách S₁S₂ đoạn d₁ = d₂ = 8cm

\(\begin{array}{*{20}{l}} {u = 2A\cos \frac{{\pi ({d_2} - {d_1})}}{\lambda }cos(2\pi ft - \frac{{\pi ({d_2} + {d_1})}}{\lambda })}\\ { = 2A\cos \frac{{\pi .(8 - 8)}}{{1,6}}cos(2\pi .50t - \frac{{\pi .(8 + 8)}}{{1,6}})}\\ { = 2Acos(100\pi t - 10\pi )}\\ { = 2Acos(100\pi t)(cm)} \end{array}\)

M′ cách S₁S₂ đoạn 8cm:

\(\Rightarrow {d_1} = {d_2} = \sqrt {{8^2} + {6^2}} = 10cm\)

\(\begin{array}{*{20}{l}} \begin{array}{l} u = 2A\cos \frac{{\pi ({d_2} - {d_1})}}{\lambda }cos(2\pi ft - \frac{{\pi ({d_2} + {d_1})}}{\lambda })\\ = 2A\cos \frac{{\pi .(10 - 10)}}{{1,6}}cos(2\pi .50t - \frac{{\pi .(10 + 10)}}{{1,6}}) \end{array}\\ { = 2Acos(100\pi t - \frac{{25\pi }}{2})}\\ { = 2Acos(100\pi t - \frac{\pi }{2})(cm)} \end{array}\)