Giải bài tập SBT Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp

Đặt một điện áp xoay chiều có giá trị hiệu dụng 50V vào hai đầu đoạn mạch gồm điện trở thuần R mắc nối tiếp với cuộn cảm thuần L. Điện áp hiệu dụng giữa hai đầu R là 30V. Điện áp hiệu dụng giữa hai đầu cuộn cảm bằng

A. 30V.                              B. 20V.

C. 10V.                              D. 40V.

Phương pháp giải

Sử dụng công thức:

 U² = U_R² + (U_L−U_C)² 

để tính U_L là:

\({{U_L} = \sqrt {{U^2} - U_R^2} }\)

Hướng dẫn giải

Ta có: U² = U_R² + (U_L−U_C)²

mà mạch điện không có tụ nên U_C=0

⇒ U²=U_R²+U_L²

\(\begin{array}{l} \Rightarrow {U_L} = \sqrt {{U^2} - U_R^2} \\ = \sqrt {{{50}^2} - {{30}^2}} = 40V \end{array}\)

- Chọn D

Đặt điện áp xoay chiều u=100√2cosωt(V)  vào hai đầu một đoạn mạch gồm cuộn cảm thuần và tụ điện mắc nối tiếp. Biết điện áp hiệu dụng giữa hai đầu tụ điện là 100Vvà điện áp giữa hai đầu đoạn mạch sớm pha so với cường độ dòng điện trong mạch. Điện áp hiệu dụng giữa hai đầu cuộn cảm bằng

A. 150V.                        B. 50V.

C. 100√2.V                    D. 200V.

Phương pháp giải

- Từ công thức: 

 U² = U_R² + (U_L−U_C)²

tính khi không có điện trở và u sớm pha hơn i

- Ta được: U_L=U+U_C

Hướng dẫn giải

- Ta có: U² = U_R² + (U_L−U_C)²

mà mạch điện không có điện trở nên UR=0

⇒U = |U_L−U_C|

- Vì điện áp giữa hai đầu đoạn mạch sớm pha so với cường độ dòng điện trong mạch

U_L>U_C ⇒U=U_L−U_C

⇒U_L=U+U_C=100+100=200V

- Chọn D

Đặt một điện áp xoay chiều u=200√2cos100πt(V) vào hai đầu một đoạn mạch gồm cuộn cảm thuần có độ tự cảm L=1π(H) và tụ điện có điện dung C=10⁻⁴/2π(F)mắc nối tiếp. Cường độ hiệu dụng của dòng điện trong đoạn mạch là

A. 2A.                            B. 1,5A.

C. 0,75A.                       D. 2√2A.

Phương pháp giải

- Tính cảm kháng và dung kháng

- Tổng trở khi R =0 được tính là:

Z=|ZL−ZC|

- Áp dụng định luật Ôm để tính I

 I=U/Z

Hướng dẫn giải

- Cảm kháng: 

Z_L=Lω=1π.100π=100Ω

- Dung kháng:

\({Z_C} = \frac{1}{{C\omega }} = \frac{1}{{\frac{{{{10}^{ - 4}}}}{{2\pi }}.100\pi }} = 200{\rm{\Omega }}\)

- Mạch không có điện trở nên R=0

⇒Z=|ZL−ZC|=|100−200|=100Ω

- Ta có: I=U/Z=200/100=2A

- Chọn A

Khi đặt hiệu điện thế không đổi 30V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm 14π(H) thì dòng điện trong mạch là dòng điện một chiều có cường độ 1A. Nếu đặt vào hai đầu đoạn mạch này điện áp xoay chiều u=150√2cos120πt(V) thì biểu thức của cường độ  dòng điện trong đoạn mạch là:

A. i=5√2cos(120πt+π/4)(A).

B. i=5√2cos(120πt−π/4)(A).

C. i=5cos(120πt−π/4)(A).

D. i=5cos(120πt+π/4)(A).

Phương pháp giải

- Tính điện trở theo công thức;

R = U_1c/I_1c

- Tính cảm kháng và dung kháng

- Áp dụng công thức tính tổng trở: 

\(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)

- Áp dụng định luật Ôm: I₀= U₀/Z để tính cường độ dòng điện

- Sử dụng công thức 

φ = φ_u−φ_i; tanφ = Z_L−Z_CR

 để tính độ lệch pha giữa điện áp và dòng điện

Hướng dẫn giải

- Chỉ có điện trở cản trở dòng điện không đổi:

\(R = \frac{{{U_{1c}}}}{{{I_{1c}}}} = \frac{{30}}{1} = 30{\rm{\Omega }}\)

- Cảm kháng: 

\({Z_L} = L\omega = \frac{1}{{4\pi }}.120\pi = 30{\rm{\Omega }}\)

- Tổng trở của mạch điện:

\(\begin{array}{l} Z = \sqrt {{R^2} + {Z_L}^2} \\ = \sqrt {{{30}^2} + {{30}^2}} = 30\sqrt 2 {\rm{\Omega }} \end{array}\)

- Ta có: 

\({I_0} = \frac{{{U_0}}}{Z} = \frac{{150\sqrt 2 }}{{30\sqrt 2 }} = 5A\)

- Độ lệch pha giữa điện áp và dòng điện:

\(\begin{array}{l} \tan \varphi = \frac{{{Z_L}}}{R} = \frac{{30}}{{30}} = 1\\ \Rightarrow \varphi = \frac{\pi }{4}rad \end{array}\)

- Ta có: 

\(\begin{array}{l} \varphi = {\varphi _u} - {\varphi _i}\\ \Rightarrow {\varphi _i} = {\varphi _u} - \varphi = - \frac{\pi }{4}(rad) \end{array}\)

- Vậy biểu thức dòng điện là:

i= 5cos(120πt−π/4) (A)

- Chọn C

Đặt một điện áp xoay chiều u=100√2cos100πt(V) vào hai đầu đoạn mạch gồm R,L,C mắc nối tiếp. Biết R=50Ω, cuộn cảm thuần có L=1π(H) và tụ điện có C=2.10⁻⁴/π(F). Cường độ hiệu dụng trong đoạn mạch này là

A. √2A.                     B. 2√2A.

C. 2A.                       D. 1A.

Phương pháp giải

- Tính cảm kháng và dung kháng

- Áp dụng công thức tính tổng trở:

\(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)

- Vận dụng công thức định luật Ôm để tính I

 I=U_Z/I=U/Z

Hướng dẫn giải

- Cảm kháng:

Z_L= Lω= 1π.100π= 100Ω

- Dung kháng:

\({Z_C} = \frac{1}{{C\omega }} = \frac{1}{{\frac{{{{2.10}^{ - 4}}}}{\pi }.100\pi }} = 50{\rm{\Omega }}\)

- Tổng trở của mạch điện:

\(\begin{array}{l} Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\ = \sqrt {{{50}^2} + {{(100 - 50)}^2}} = 50\sqrt 2 {\rm{\Omega }} \end{array}\)

- Cường độ dòng điện hiệu dụng:

\(I = \frac{U}{Z} = \frac{{100}}{{50\sqrt 2 }} = \sqrt 2 A\)

- Chọn A

Đặt điện áp u=U√2cosωt vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Biết ω=1√LC. Tổng trở của đoạn mạch này bằng

A. R.                             B. 3R.

C. 0,5R.                        D. 2R.

Phương pháp giải

- Theo điều kiện đề bài:

ω=1√LC ta tính được Z_L = Z_C

- Sử dụng công thức tính tổng trở: 

\(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)

Hướng dẫn giải

- Ta có

\(\begin{array}{*{20}{l}} {\omega = \frac{1}{{\sqrt {LC} }}}\\ { \Leftrightarrow {\omega ^2} = \frac{1}{{LC}}}\\ { \Leftrightarrow L\omega = \frac{1}{{C\omega }} \Leftrightarrow {Z_L} = {Z_C}} \end{array}\)

- Tổng trở: 

\(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = R\)

- Chọn A

Đặt điện áp xoay chiều u=U₀cosωt vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Gọi i là cường độ dòng điện tức thời trong đoạn mạch; u₁, u₂, u₃ lần lượt là điện áp tức thời giữa hai đầu điện trở, giữa hai đầu cuộn cảm và giữa hai đầu tụ điện. Hệ thức đúng là:

A. i= u₂ωL.

B. i= u₁R.

C. i= u₃ωC.

D. \(i = \frac{u}{{{R^2} + {{(\omega L - \frac{1}{{\omega C}})}^2}}}.\)

Phương pháp giải

Sử dụng lí thuyết về dòng điện tức thời và điện áp tức thời

Hướng dẫn giải

- Trong mạch điện chỉ chứa R, dòng điện và điện áp cùng pha nên vậy giả sử:

\(\begin{array}{l} i = {I_0}\cos (\omega t + \varphi )\\ \Rightarrow {u_1} = {U_{0R}}\cos (\omega t + \varphi )\\ \Rightarrow \frac{{{u_1}}}{i} = \frac{{{U_{0R}}}}{{{I_0}}} = R \end{array}\)

- Chọn B

Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi vào hai đầu đoạn mạch có R,L,C mắc nối tiếp. Khi trong đoạn mạch xảy ra hiện tượng cộng hưởng điện, phát biểu nào sau đây là sai?

A. Cường độ dòng điện hiệu dụng trong đoạn mạch không phụ thuộc vào giá trị điện trở R.

B. Cường độ dòng điện hiệu dụng trong đoạn mạch đạt giá trị cực đại.

C. Điện áp hiệu dụng giữa hai bản tụ điện và giữa hai đầu cuộn cảm thuần có cùng giá trị.

D. Cường độ dòng điện trong đoạn mạch cùng pha với điện áp giữa hai đầu đoạn mạch.

Phương pháp giải

Để trả lời câu hỏi này, cần nắm được các đặc điểm của hiện tượng cộng hưởng

Hướng dẫn giải

- A sai vì: 

- Khi có hiện tưởng cộng hưởng điện:

 dòng điện đạt cực đại I_max= U/R

⇒ có phụ thuộc vào R

Đặt điện áp xoay chiều u=U₀cos100πt (U₀ không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở 50Ω, cuộn cảm thuần có độ tự cảm 0,318H và tụ điện có điện dung thay đổi được. Để cường độ dòng điện hiệu dụng trong đoạn mạch đạt giá trị cực đại thì phải điều chỉnh điện dung của tụ điện tới giá trị bằng

A. 42,48μF.                   B. 47,74μF.

C. 63,72μF.                   D. 31,86μF.

Phương pháp giải

Áp dụng điều kiện cộng hưởng để tìm điện dung C

Hướng dẫn giải

- Khi có hiện tưởng cộng hưởng điện dòng điện đạt cực đại

- Điều kiện xảy ra cộng hưởng điện là

\(\begin{array}{*{20}{l}} {{Z_L} = {Z_C} \Leftrightarrow L\omega = \frac{1}{{C\omega }}}\\ \begin{array}{l} \Leftrightarrow C = \frac{1}{{L{\omega ^2}}} = \frac{1}{{0,318{\pi ^2}}}\\ \Rightarrow C = {31,86.10^{ - 6}}F = 31,86\mu F \end{array} \end{array}\)

- Chọn D

Cho mạch gồm điện trở R=30√3Ω nối tiếp với tụ điện C=1/3000π(F), điện áp tức thời ở hai đầu đoạn mạch là u=120√2cos100πt(V).

a) Viết biểu thức của cường độ dòng điện tức thời trong mạch.

b) Xác định điện áp hiệu dụng ở hai đầu điện trở R và ở hai đầu tụ điện C.

Phương pháp giải

a) Tính  tổng trở: 

\(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)

- Định luật Ôm cho đoạn mạch RLC mắc nối tiếp: 

I₀=U₀/Z

- Biểu thức tính độ lệch pha giữa điện áp và dòng điện:

\(\begin{array}{l} \varphi = {\varphi _u} - {\varphi _i} \end{array}\);  \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)

b) Công thức tính điện áp hiệu dung:

 U_R= I.R  và U_C= I.Z_C

Hướng dẫn giải

a) Dung kháng là:

\({Z_C} = \frac{1}{{C\omega }} = \frac{1}{{\frac{1}{{3000\pi }}.100\pi }} = 30{\rm{\Omega }}\)

- Tổng trở của mạch điện:

\(Z = \sqrt {{R^2} + {Z_C}^2} = \sqrt {{{(30\sqrt 3 )}^2} + {{30}^2}} = 60{\rm{\Omega }}\)

- Ta có: I₀= U₀/Z = 120√2/60 = 2√2A

- Độ lệch pha giữa điện áp và dòng điện:

\(\begin{array}{l} \tan \varphi = - \frac{{{Z_C}}}{R} = - \frac{{30}}{{30\sqrt 3 }} = - \frac{1}{{\sqrt 3 }}\\ \Rightarrow \varphi = - \frac{\pi }{6}rad \end{array}\)

- Ta có:

\(\begin{array}{l} \varphi = {\varphi _u} - {\varphi _i}\\ \Rightarrow {\varphi _i} = {\varphi _u} - \varphi = \frac{\pi }{6}(rad) \end{array}\)

- Vậy biểu thức dòng điện là:

 i=2√2cos(100πt+π/6)(A)

b) Cường độ dòng điện hiệu dụng:

I = I₀/√2 = 2A

- Điện áp giữa hai đầu điện trở: 

U_R= I.R = 2.30√3 = 60√3V

- Điện áp giữa hai đầu tụ: 

U_C = I.Z_C = 2.30 = 60V

Cho mạch gồm điện trở R=40Ω nối tiếp với cuộn cảm thuần có L=0,4π(H); điện áp tức thời ở hai đầu đoạn mạch u=80cos100πt(V).

a) Viết biểu thức của cường độ dòng điện tức thời trong mạch.

b) Xác định điện áp hiệu dụng ở hai đầu điện trở R và ở hai đầu cuộn cảm L.

Phương pháp giải

a) Tính cảm kháng: Z_L= Lω

- Tính tổng trở theo công thức: 

\(Z = \sqrt {{R^2} + {{({Z_L})}^2}} \)

- Sử dụng định luật Ôm để tinh cường độ 

I₀=U₀/Z

- Sử dụng biểu thức:

\(\begin{array}{l} \varphi = {\varphi _u} - {\varphi _i} \end{array}\);  \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)

 để tính độ lệch pha giữa điện áp và dòng điện

b) Sử dụng công thức tính điện áp hiệu dung: 

U_R=I.R  và U_L= I.Z_L

Hướng dẫn giải

a) Cảm kháng:

Z_L= Lω= 0,4π.100π= 40Ω

- Tổng trở của mạch điện:

\(\begin{array}{l} Z = \sqrt {{R^2} + {Z_L}^2} \\ = \sqrt {{{40}^2} + {{40}^2}} = 40\sqrt 2 {\rm{\Omega }} \end{array}\)

- Cường độ dòng điện hiệu dụng:

\({I_0} = \frac{{{U_0}}}{Z} = \frac{{80}}{{40\sqrt 2 }} = \sqrt 2 A\)

- Độ lệch pha giữa điện áp và dòng điện:

\(\begin{array}{l} \tan \varphi = \frac{{{Z_L}}}{R} = \frac{{40}}{{40}} = 1\\ \Rightarrow \varphi = \frac{\pi }{4}rad \end{array}\)

- Ta có:

\(\begin{array}{l} \varphi = {\varphi _u} - {\varphi _i}\\ \Rightarrow {\varphi _i} = {\varphi _u} - \varphi = - \frac{\pi }{4}(rad) \end{array}\)

- Vậy biểu thức dòng điện là: 

i= √2cos(100πt−π/4) (A)

b) 

- Điện áp giữa hai đầu điện trở: 

U_R= I.R= 1.40= 40V

- Điện áp giữa hai đầu cuộn cảm: 

U_L= I.Z_L= 1.40= 40V

Cho mạch gồm điện trở R=30Ω nối tiếp với cuộn cảm L; điện áp tức thời ở hai đầu đoạn mạch u=120cos100πt(V). Điện áp hiệu dụng ở hai đầu cuộn cảm bằng 60V.

a) Xác định Z_L.

b) Viết biểu thức của cường độ dòng điện tức thời i.

Phương pháp giải

a) Tính điện trở bằng cách:

- Dựa vào công thức tính hiệu điện thế toàn mạch suy ra U_R

_{\({{U_L} = \sqrt {{U^2} - U_L^2} }\)}

- Từ R tìm cường độ I: I=U_R/R

- Tính Z_L theo công thức: Z=U_L/I

b) Để viết phương trình i, cùng với các thông số đã có, ta dựa vào công thức:

\(\varphi = {\varphi _u} - {\varphi _i};\,\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)

để tính độ lệch pha giữa điện áp và dòng điện 

Hướng dẫn giải

a)-  Hiệu điện thế:

\(\begin{array}{l} {U^2} = U_R^2 + U_L^2\\ \Rightarrow {U_R} = \sqrt {{U^2} - U_L^2} \\ = \sqrt {{{(60\sqrt 2 )}^2} - {{60}^2}} = 60V \end{array}\)

- Cường độ dòng điện:

\(\begin{array}{l} I = \frac{{{U_R}}}{R} = \frac{{60}}{{30}} = 2A\\ \Rightarrow {I_0} = 2\sqrt 2 A \end{array}\)

\(I = \frac{{{U_L}}}{{{Z_L}}} \Rightarrow {Z_L} = \frac{{{U_L}}}{I} = \frac{{60}}{2} = 30{\rm{\Omega }}\)

b) Độ lệch pha giữa điện áp và dòng điện:

\(\tan \varphi = \frac{{{Z_L}}}{R} = \frac{{60}}{{60}} = 1 \Rightarrow \varphi = \frac{\pi }{4}rad\)

- Ta có:

\(\begin{array}{l} \varphi = {\varphi _u} - {\varphi _i}\\ \Rightarrow {\varphi _i} = {\varphi _u} - \varphi = - \frac{\pi }{4}(rad) \end{array}\)

- Vậy biểu thức dòng điện là:

 i= 2√2cos (100πt−π/4) (A)

Cho mạch gồm điện trở R nối tiếp với tụ điện C=1/3000πF;điện áp tức thời ở hai đầu đoạn mạch u=120√2cos100πt(V). Điện áp hiệu dụng ở hai đầu điện trở là 60V.

a) Xác định R.

b) Viết biểu thức của cường độ dòng điện tức thời i.

Phương pháp giải

- Áp dụng công thức Z_C=1/ωC để tính dung kháng

a) Tính điện trở bằng cách:

- Dựa vào công thức tính hiệu điện thế toàn mạch suy ra U_C

_{\({{U_C} = \sqrt {{U^2} - U_R^2} }\)}

- Từ U_C tìm cường độ I: I=U_C/Z_C

- Tính điện trở theo công thức: R=U_R/I

b) Để viết phương trình i, cùng với các thông số đã có, ta dựa vào công thức:

\(\varphi = {\varphi _u} - {\varphi _i};\,\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)

để tính độ lệch pha giữa điện áp và dòng điện 

Huớng dẫn giải

- Dung kháng là:

\({Z_C} = \frac{1}{{C\omega }} = \frac{1}{{\frac{1}{{3000\pi }}.100\pi }} = 30{\rm{\Omega }}\)

a) Ta có: 

\(\begin{array}{l} {U^2} = U_R^2 + U_C^2\\ \Rightarrow {U_C} = \sqrt {{U^2} - U_R^2} \\ = \sqrt {{{120}^2} - {{60}^2}} = 60\sqrt 3 V \end{array}\)

- Cường độ dòng điện:

\(\begin{array}{l} I = \frac{{{U_C}}}{{{Z_C}}} = \frac{{60\sqrt 3 }}{{30}} = 2\sqrt 3 A\\ \Rightarrow {I_0} = 2\sqrt 6 A\\ I = \frac{{{U_R}}}{R} \Rightarrow R = \frac{{{U_R}}}{I} = \frac{{60}}{{2\sqrt 3 }} = 10\sqrt 3 {\rm{\Omega }} \end{array}\)

b) Độ lệch pha giữa điện áp và dòng điện:

\(\begin{array}{l} \tan \varphi = - \frac{{{Z_C}}}{R} = - \frac{{30}}{{10\sqrt 3 }} = - \sqrt 3 \\ \Rightarrow \varphi = - \frac{\pi }{3}rad \end{array}\)

- Ta có:

\(\begin{array}{l} \varphi = {\varphi _u} - {\varphi _i}\\ \Rightarrow {\varphi _i} = {\varphi _u} - \varphi = \frac{\pi }{3}(rad) \end{array}\)

- Vậy biểu thức dòng điện là:

 i= 2√6cos(100πt+π/3) (A)

Cho mạch điện gồm điện trở R=30Ω nối tiếp với hai tụ điện C₁=1/3000π(F); C₂=1/1000π(F) nối tiếp nhau (H.14.1). Điện áp tức thời ở hai đầu đoạn mạch là u=100√2cos100πt(V).

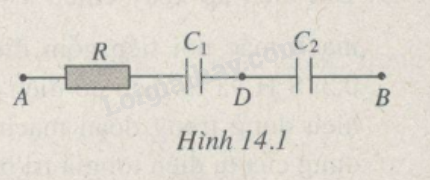
a) Xác định I.

b) Xác định U_AD;U_DB.

Phương pháp giải

- Tính dung kháng

- Áp dụng ông thức tính điện dung tương đương trong ghép nối tiếp: 

\(\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}}\)

- Tính tổng trở theo công thức: 

\(Z = \sqrt {{R^2} + {Z_C}^2} \)

- Định luật Ôm để tính I và U:

I = U/Z và U = I.Z

Hướng dẫn giải

- Dung kháng là:

\(\begin{array}{l} {Z_{{C_1}}} = \frac{1}{{{C_1}\omega }} = \frac{1}{{\frac{1}{{3000\pi }}.100\pi }} = 30{\rm{\Omega }}\\ {Z_{{C_2}}} = \frac{1}{{{C_2}\omega }} = \frac{1}{{\frac{1}{{1000\pi }}.100\pi }} = 10{\rm{\Omega }} \end{array}\)

- Ta có C₁ nối tiếp với C₂ nên điện dung tương đương: 

\(\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}}\)

Mà

\(\begin{array}{*{20}{l}} {{Z_C} = \frac{1}{{C\omega }} \Rightarrow {Z_C} \sim \frac{1}{C}}\\ { \Rightarrow {Z_C} = {Z_{{C_1}}} + {Z_{{C_2}}} = 30 + 10 = 40{\rm{\Omega }}} \end{array}\)

- Tổng trở là:

\(Z = \sqrt {{R^2} + {Z_C}^2} = \sqrt {{{30}^2} + {{40}^2}} = 50{\rm{\Omega }}\)

- Cường độ dòng điện hiệu dụng:

I= U/Z= 100/50= 2A

b) Ta có:

\(\begin{array}{l} {U_{AD}} = I.{Z_{R{C_1}}} = I.\sqrt {{R^2} + Z_{{C_1}}^2} \\ = 2\sqrt {{{30}^2} + {{30}^2}} = 60\sqrt 2 V \end{array}\)

U_DB= I.Z_C= 2.10= 20V

Cho mạch điện gồm ba phần tử mắc nối tiếp (H.14.2) L₁=0,1π(H); R=40Ω; L₂=0,3π(H). Điện áp tức thời ở hai đầu đoạn mạch u=160√2cos100πt(V).

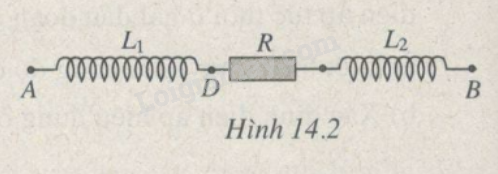
a) Viết biểu thức của i.

b) Xác định U_DB.

Phương pháp giải

a)  Viết biểu thức của i

- Tính tổng trở theo công thức: Z= Lω để tính cảm kháng

\(Z = \sqrt {{R^2} + {Z_L}^2} \)

- Áp dụng định luật Ôm: I=U/Z để tính I

- Sử dụng công thức 

\(\varphi = {\varphi _u} - {\varphi _i};\,\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)

tính độ lệch pha giữa điện áp và dòng điện

b) Áp dụng công thức: U = I.Z để tính hiệu điện thế

Hướng dẫn giải

- Cảm kháng là:

Z_L1= L₁ω= 0,1π.100π= 10Ω

Z_L2= L₂ω= 0,3π.100π= 30Ω

- Tổng trở:

\(\begin{array}{l} Z = \sqrt {{R^2} + {{({Z_{{L_1}}} + {Z_{{L_2}}})}^2}} \\ = \sqrt {{{40}^2} + {{(10 + 30)}^2}} = 40\sqrt 2 {\rm{\Omega }} \end{array}\)

- Cường độ dòng điện hiệu dụng:

\(I = \frac{U}{Z} = \frac{{160}}{{40\sqrt 2 }} = 2\sqrt 2 A \Rightarrow {I_0} = 4A\)

- Độ lệch pha giữa điện áp và dòng điện:

\(\begin{array}{l} \tan \varphi = \frac{{{Z_{{L_1}}} + {Z_{{L_2}}}}}{R} = \frac{{30 + 10}}{{40}} = 1\\ \Rightarrow \varphi = \frac{\pi }{4}rad \end{array}\)

- Ta có :

\(\begin{array}{l} \varphi = {\varphi _u} - {\varphi _i}\\ \Rightarrow {\varphi _i} = {\varphi _u} - \varphi = - \frac{\pi }{4}(rad) \end{array}\)

- Vậy biểu thức dòng điện là:

 i= 4cos(100πt−π/4) (A)

 b) Ta có:

\(\begin{array}{l} {U_{DB}} = I.{Z_{R{L_2}}} = I.\sqrt {{R^2} + Z_{{L_2}}^2} \\ = 2\sqrt 2 .\sqrt {{{40}^2} + {{30}^2}} = 100\sqrt 2 V \end{array}\)