Giải bài tập SBT Vật Lí 11 Bài 21: Từ trường của dòng điện chạy trong các dây dẫn có hình dạng đặc biệt

Chỉ ra ý đúng.

Cảm ứng từ do dòng điện chạy trong dây dẫn thẳng dài gây ra tại một điểm M có độ lớn tăng lên khi

A. điểm M dịch chuyển theo hướng vuông góc với dây và rời xa dây.

B. điểm M dịch chuyển theo hướng vuông góc với dây và lại gần dây.

C. điểm M dịch chuyển theo hướng song song với dây.

D. điểm M dịch chuyển theo một đường sức từ của dòng điện. 

Phương pháp giải

Để trả lời câu hỏi này cần nắm được đặc điểm của cảm ứng từ

Hướng dẫn giải

- Cảm ứng từ do dòng điện chạy trong dây dẫn thẳng dài gây ra tại một điểm M có độ lớn tăng lên khi điểm M dịch chuyển theo hướng vuông góc với dây và lại gần dây. 

- Đáp án B

Cảm ứng từ do dòng điện chạy trong dây dẫn uốn thành vòng tròn gây ra tại tâm O của vòng dây có độ lớn giảm khi

A. cường độ dòng điện tăng dần.

B. cường độ dòng điện giảm dần.

C. số vòng dây dẫn có cùng tâm O tăng dần.

D. đường kính của vòng dây dẫn giảm dần. 

Phương pháp giải

Công thức cảm ứng từ đối với vòng dây tâm O: B = 2.10^-7 I/r

⇒ cảm ứng từ B tỉ lệ thuận với cường độ dòng điện I

Hướng dẫn giải

- Cảm ứng từ do dòng điện chạy trong dây dẫn uốn thành vòng tròn gây ra tại tâm O của vòng dây có độ lớn giảm khi cường độ dòng điện giảm dần. 

- Đáp án B

Cảm ứng từ do dòng điện chạy qua ống dây dẫn hình trụ gây ra ở bên trong ống dây có độ lớn tăng lên khi

A. độ dài của ống dây hình trụ tăng dần.

B. đường kính của ống dây hình trụ giảm dần.

C. số vòng dây quấn trên mỗi đơn vị dài của ống dây hình trụ tăng dần.

D. cường độ dòng điện chạy qua ống dây hình trụ giảm dần. 

Phương pháp giải

Công thức cảm ứng từ qua ống dây dẫn hình trụ: B = 2π.10^-7 NI/l = 4π.10^-7.nI

⇒ cảm ứng từ B tỉ lệ thuận với số vòng dây n

Hướng dẫn giải

- Cảm ứng từ do dòng điện chạy qua ống dây dẫn hình trụ gây ra ở bên trong ống dây có độ lớn tăng lên khi số vòng dây quấn trên mỗi đơn vị dài của ống dây hình trụ tăng dần. 

- Đáp án C

Dòng điện cường độ 12 A chạy qua một dây dẫn thẳng dài gây ra tại điểm M trong không khí một từ trường có cảm ứng từ là 1,6.10^-5 T. Xác định khoảng cách từ điểm M đến dây dẫn thẳng.

A. 15 cm.                         B. 1,5 cm.    

C. 150 cm.                       D. 0,15 cm. 

Phương pháp giải

Tính khoảng cách từ điểm M đến dây dẫn thẳng theo công thức: 

\(r = {2.10^{ - 7}}.\frac{I}{B} \)

Hướng dẫn giải

- Áp dụng công thức B = 2.10^-7 I/r

Ta suy ra khoảng cách từ điểm M đến dây dẫn thẳng có dòng điện cường độ I = 12A:

\(r = {2.10^{ - 7}}.\frac{I}{B} = {2.10^{ - 7}}.\frac{{12}}{{1,{{6.10}^{ - 5}}}} = 15cm\)

- Đáp án A

Một dòng điện chạy trong một vòng dây dẫn bán kính 5,8 cm gây ra tại tâm của vòng dây một từ trường có cảm ứng từ là 1,3.10^-4 T. Xác định cường độ dòng điện chạy trong vòng dây dẫn này.

A. 1,2 A.                B. 20 A.                

C. 12 A.                 D. 2,5 A. 

Phương pháp giải

Tính cường độ dòng điện theo công thức:

\(I = \frac{{Br}}{{2\pi {{.10}^{ - 7}}}} A\)

Hướng dẫn giải

- Áp dụng công thức B = 2π.10^-7 I/r

Ta tìm được cường độ dòng điện chạy trong vòng dây dẫn:

\(I = \frac{{Br}}{{2\pi {{.10}^{ - 7}}}} = \frac{{1,{{3.10}^{ - 4}}.5,{{8.10}^{ - 2}}}}{{2.3,{{14.10}^{ - 7}}}} = 12A\)

- Đáp án C

Một ống dây dẫn hình trụ dài 31,4 cm (không lõi sắt) gồm 1200 vòng có dòng điện cường độ 2,5 A chạy qua. Xác định cảm ứng từ bên trong ống dây này. Cho biết đường kính của ống dây khá nhỏ so với độ dài của nó.

A. 2.1T.                 B.0,12.10^-3T.                           

C. 1,2T.                D. 12.10^-3T. 

Phương pháp giải

Tính cảm ứng từ bên trong ống dây theo công thức:

B = 2π.10^-7 NI/l 

Hướng dẫn giải

- Áp dụng công thức B = 2π.10^-7 NI/l ta tìm được cảm ứng từ bên trong ống dây dẫn:

\(B = 4.3,{14.10^{ - 7}}.\frac{{1200}}{{31,{{4.10}^{ - 2}}}}.2,5 = {12.10^{ - 3}}T\)

- Đáp án D

Dòng điện chạy qua một dây dẫn thẳng dài đặt nằm ngang trong không khí gây ra tại một điểm cách nó 4,5 cm một cảm ứng từ có độ lớn 2,8.10^-4 T. Xác định :

a) Cường độ của dòng điện chạy qua dây dẫn thẳng.

b) Độ lớn của cảm ứng từ do dòng điện này gây ra tại điểm cách nó 10 cm. 

Phương pháp giải

a) Cường độ của dòng điện được tính theo công thức:

\(I = \frac{{{B_1}{r_1}}}{{{{2.10}^{ - 7}}}}\)

b) Độ lớn cảm ứng được tính theo công thức:

\({B_2} = {2.10^{ - 7}}\frac{I}{{{r_2}}} \)

Hướng dẫn giải

Áp dụng công thức B = 2.10^-7 I/r ta suy ra

a) Cường độ của dòng điện chạy qua dây dẫn thẳng dài đặt nằm ngang trong không khí gây ra cảm ứng từ có độ lớn B₁ = 2,8.10^-4 T tại điểm M cách nó một khoảng r₁ = 4,5cm:

\(I = \frac{{{B_1}{r_1}}}{{{{2.10}^{ - 7}}}} = \frac{{2,{{8.10}^{ - 4}}.4,{{5.10}^{ - 2}}}}{{{{2.10}^{ - 7}}}} = 63A\)$$

b) Cảm ứng từ do dòng điện có cường độ I = 63 A chạy qua dây dẫn thẳng dài đặt nằm ngang trong không khí gây ra tại điểm N cách nó một khoảng r₂ = 10 cm :

\({B_2} = {2.10^{ - 7}}\frac{I}{{{r_2}}} = {2.10^{ - 7}}.\frac{{63}}{{{{10.10}^{ - 2}}}} = 1,{26.10^{ - 4}}T\)

Một dây dẫn thẳng dài 1,4 m đặt trong từ trường đều có cảm ứng từ 0,25 T. Khi dòng điện cường độ 12 A chạy qua dây dẫn thì dây dẫn này bị tác dụng một lực bằng 2,1 N. Xác định góc hợp bởi hướng của dòng điện chạy qua dây dẫn và hướng của cảm ứng từ. 

Phương pháp giải

Dựa vào công thức tính lực từ: F = BIlsinα để tìm góc hợp giữa I và B

Hướng dẫn giải

- Gọi α là góc hợp bởi hướng của dòng điện chạy qua dây dẫn và hướng của cảm ứng từ. Lực từ do từ trường tác dụng lên dòng điện chạy qua dây dẫn thẳng có độ lớn tính theo công thức:

F = BIlsinα

- Từ đó suy ra :  

\(\begin{array}{l} \sin \alpha = \frac{F}{{BI\ell }} = \frac{{2,1}}{{0,25.12.1,4}} = 0,50\\ \Rightarrow \alpha = {30^0} \end{array}\)

Cho dòng điện cường độ 20 A chạy qua một dây đồng có tiết diện 1,0 mm² được uốn thành một vòng tròn đặt trong không khí. Khi đó cảm ứng từ tại tâm của vòng dây đồng có độ lớn bằng 2,5.10^-4 T. Cho biết dây đồng có điện trở suất là l,7.10^-8 Ω.m. Xác định hiệu điện thế giữa hai đầu vòng dây đồng. 

Phương pháp giải

- Tính bán kính vòng dây theo công thức:

\(r = 2.3,{14.10^{ - 7}}.\frac{I}{B} \)

- Áp dụng công thức:

\(U = I\rho \frac{{2\pi r}}{S}\) để tính hiệu điện thế

Hướng dẫn giải

- Áp dụng công thức B = 2.10^-7 I/r ta suy ra bán kính vòng dây:

\(r = 2.3,{14.10^{ - 7}}.\frac{I}{B} = 2.3,{14.10^{ - 7}}.\frac{{20}}{{2,{{5.10}^{ - 4}}}} \approx 5,0cm\)$$

- Hiệu điện thế giữa hai đầu dây của vòng dây đồng tính theo công thức:

\(U = {\rm{IR}} = I\rho \frac{\ell }{S} = I\rho \frac{{2\pi r}}{S}\)

- Thay số ta tìm được:

\(U = 20.1,{7.10^{ - 8}}.\frac{{2.3,14.5,{{0.10}^{ - 2}}}}{{{{1.10}^{ - 6}}}} \approx 107mV\)

Xác định số vòng dây có trên mỗi cm dọc theo chiều dài của ống dây dẫn hình trụ (không lõi sắt) để cảm ứng từ bên trong ống dây dẫn có độ lớn không nhỏ hơn 8,2.10^-3T khi dòng điện trong ống dây có cường độ 4,35 A. 

Phương pháp giải

- Tính cảm ứng từ theo công thức:

B = 2π.10^-7 NI/l = 4π.10^-7.nI

- Số vòng dây được tính theo công thức: n = N/l

⇒ số vòng dây quấn trên mỗi cm dọc theo chiều dài của ống dây

Hướng dẫn giải

- Áp dụng công thức B = 2π.10^-7 NI/l = 4π.10^-7.nI

Trong đó n = N/l  là số vòng dây quấn trên mỗi đơn vị dài của ống dây dẫn.

- Như vậy, nếu muốn B ≥ 8,2.10^-3 T, thì ta phải có :

B = 4.3,14.10^-7n.4,35 ≥ 8,2.10^-3

- Từ đó suy ra số vòng dây quấn trên mỗi đơn vị dài của ống dây dẫn:

\(n \ge \frac{{8,{{2.10}^{ - 3}}}}{{4.3,{{14.10}^{ - 7}}.4,35}} = 1500\) vòng/m = 15 vòng/cm

Hai dây dẫn thẳng dài có dòng điện chạy qua được đặt song song và cách nhau 12 cm trong không khí. Dây dẫn thứ nhất dài 2,8 m bị dây dẫn thứ hai hút bởi một lực 3,4.10^-3 N khi dòng điện trong dây dẫn thứ nhất có cường độ 58 A. Xác định cường độ và chiều dòng điện chạy trong dây dẫn thứ hai. 

Phương pháp giải

Để xác định cường độ dòng điện, ta làm như sau:

- Áp dụng công thức tính cảm ứng từ:

\({B_2} = {2.10^{ - 7}}.\frac{{{I_2}}}{d}\)

- Áp dụng công thức tính lực điện:

F₂ = B₂I₁l₁

- Tính cường độ dòng điện theo công thức:

\({I_2} = \frac{{{F_2}d}}{{{{2.10}^{ - 7}}.{I_1}{\ell _1}}} \)

Hướng dẫn giải

Cảm ứng từ \(\vec B\) do dòng điện cường độ I₂ chạy trong dây dẫn thứ hai gây ra tại điểm M cách nó một khoảng d = 12 cm nằm trên dây dẫn thứ nhất, có phương vuông góc dây dẫn thứ nhất và có độ lớn bằng:

\({B_2} = {2.10^{ - 7}}.\frac{{{I_2}}}{d}\)$$

- Dòng điện cường độ I₁ chạy trong dây dẫn thứ nhất có độ dài l₁ = 2,8 m bị cảm ứng từ \(\overrightarrow {{B_2}} \)  hướng vuông góc với nó hút bởi một lực F₂ = 3,4.10^-3 N có phương, chiều xác định theo quy tắc bàn tay trái và có độ lớn bằng :  

F₂ = B₂I₁l₁

- Vì hai dòng điện I₁ và I₂ chạy trong hai dây dẫn thẳng song song hút nhau, nên hai dòng điện này phải có chiều giống nhau.

- Thay B₂ vào công thức của F₂, ta tìm được cường độ dòng điện chạy trong dây dẫn thứ hai:

\({I_2} = \frac{{{F_2}d}}{{{{2.10}^{ - 7}}.{I_1}{\ell _1}}} = \frac{{3,{{4.10}^{ - 3}}{{.12.10}^{ - 2}}}}{{{{2.10}^{ - 7}}.58.2,8}} \approx 12,6A\)

Hai dây dẫn thẳng dài, đặt song song cách nhau 10 cm trong không khí. Dòng điện chạy qua hai dây dẫn theo chiều ngược nhau và có cùng cường độ bằng 5,0 A. Xác định cảm ứng từ tại điểm nằm cách đều hai dây dẫn một đoạn 10 cm. 

Phương pháp giải

- Vận dụng quy tắc nắm tay phải đển xác định chiều của cảm ứng từ B₁ và B₂

- Từ hình vẽ nhận thấy \(\overrightarrow {{B_1}} \) và  \(\overrightarrow {{B_2}} \) hợp nhau một góc 120^o

- Áp dung công thức:

\({B_1} = {B_2} = {2.10^{ - 7}}.\frac{{{I_1}}}{a} \) để tính độ lớn cảm ứng từ

Hướng dẫn giải

Giả sử hai dòng điện I₁ và I₂ chạy ngược chiều nhau qua hai dây dẫn song song và vuông góc với mặt phẳng Hình 21.1G.

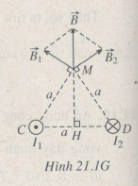
- Tại M : Vectơ cảm ứng từ  \(\overrightarrow {{B_1}} \) do dòng điện I₁ gây ra có gốc tại M, vuông góc với MC và có chiểu như hình vẽ. Vectơ cảm ứng từ  \(\overrightarrow {{B_2}} \)  do dòng điện I₂ gây ra có gốc tại M, vuông góc MD và có chiều như hình vẽ.

- Nhận xét thấy CMD là tam giác đều có cạnh a và góc (CMD) = 60° , nên góc giữa \(\overrightarrow {{B_1}} \)  và  \(\overrightarrow {{B_2}} \)  tại M bằng (\({B_1}M{B_2}\)$$ ) = 120°.

- Hơn nữa, \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) lại có cùng độ lớn :

\({B_1} = {B_2} = {2.10^{ - 7}}.\frac{{{I_1}}}{a} = {2.10^{ - 7}}.\frac{{5,0}}{{{{10.10}^{ - 2}}}} = 1,{0.10^{ - 5}}T\)$$

- Do đó vectơ cảm ứng từ tổng hợp \(\vec B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \) tại M sẽ nằm trùng với đường chéo của hình bình hành và đồng thời còn là hình thoi (vì B₁ = B₂).

- Như vậy, vectơ  sẽ nằm trên đường phân giác của góc (\({B_1}M{B_2}\)), hướng lên trên và có phương vuông góc với đoạn CD.

- Mặt khác, vì góc \(\widehat {BM{B_1}} = \widehat {BM{B_2}} = {60^o}\) nên tam giác tạo bởi \(\left( {\vec B,\overrightarrow {{B_1}} } \right)\) hoặc  \(\left( {\vec B,\overrightarrow {{B_2}} } \right)\) là đều, có các cạnh bằng nhau :

B = B₁ = B₂ = 1,0.10^-5 T