Giải bài tập SBT Vật Lí 10 Bài tập cuối chương III: Cân bằng và chuyển động của vật rắn
Cùng eLib ôn tập kiến thức và rèn luyện phương pháp giải các bài tập cuối chương III: Cân bằng và chuyển động của vật rắn trong nội dung Hướng dẫn giải bài tập dưới đây. Hy vọng đây sẽ là tài liệu hữu ích với các em học sinh.
Mục lục nội dung
1. Giải bài III.1 trang 51 SBT Vật lý 10
2. Giải bài III.2 trang 51 SBT Vật lý 10
3. Giải bài III.3 trang 51 SBT Vật lý 10
4. Giải bài III.4 trang 52 SBT Vật lý 10
5. Giải bài III.5 trang 52 SBT Vật lý 10
6. Giải bài III.6 trang 52 SBT Vật lý 10
7. Giải bài III.7 trang 52 SBT Vật lý 10
8. Giải bài III.8 trang 53 SBT Vật lý 10
9. Giải bài III.9 trang 53 SBT Vật lý 10

1. Giải bài III.1 trang 51 SBT Vật lý 10
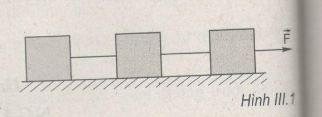
Có ba khối giống hệt nhau được nối với nhau bằng hai dây và được đặt trên mặt phẳng nằm ngang không ma sát (H.III.l). Hệ vật được tăng tốc bởi lực F. Hợp lực tác dụng lên khối giữa là bao nhiêu ?
A. 0. B. F. C. 2F/3. D. F/3
Phương pháp giải
- Áp dụng công thức: a=F/m để tính gia tốc
- Tính lực cho từng vật theo công thức: T=F=m.a
Hướng dẫn giải
Thứ tự các vật tư trái sang phải là 1 - 2 - 3
- Gia tốc của hệ vật: a=F/3m
- Xét riêng từng vật:
+ Với vật 1, lực tác dụng lên nó là lực căng T1
\({T_1} = {m_1}a = m.\frac{F}{{3m}} = \frac{F}{3}\)
+ Với vật 3, lực tác dụng lên nó bao gồm lực F và lực căng T2
\(\begin{array}{l} F - {T_2} = {m_2}a = m.\frac{F}{{3m}} = \frac{F}{3}\\ \Rightarrow {T_2} = F - \frac{F}{3} = \frac{{2F}}{3} \end{array}\)
+ Hợp lực tác dụng lên vật 2.
\({T_2} - {T_1} = \frac{{2F}}{3} - \frac{F}{3} = \frac{F}{3}\)
- Chọn đáp án D
2. Giải bài III.2 trang 51 SBT Vật lý 10
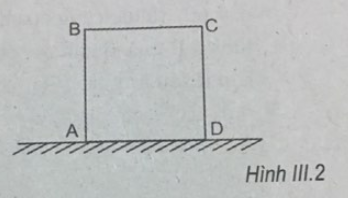
Một hình lập phương tiết diện ABCD, có trọng lượng 50N đặt trên mặt bàn nằm ngang (H.III.2). Phải tác dụng vào hình này một lực đẩy có phương song song với AD và có độ lớn tối thiểu bằng bao nhiêu để hình quay quanh D còn A bênh lên khỏi mặt bàn?
A. 50 N
B. 25 N
C. 12,5 N
D. 2,5 N
Phương pháp giải
Để giữ cho vật quay quanh D còn A bênh lên khỏi mặt bàn thì lực phải có độ lớn ít nhất bằng một nửa trọng lượng vật
Hướng dẫn giải
- Độ lớn tối thiểu của lực là: F=P/2=50/2=25N
- Chọn đáp án B
3. Giải bài III.3 trang 51 SBT Vật lý 10
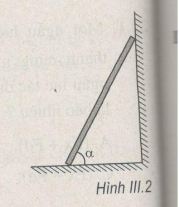
Một thanh đồng chất, dài L, trọng lượng P tựa vào tường không ma sát. Mặt sàn nhám và có hệ số ma sát trượt là µ. Thang đang đứng yên ở vị trí có góc nghiêng so với sàn là α (H.III.2). Khi giảm góc nghiêng α xuống đến quá giá trị α1 thì thang bắt đầu trượt. Coi một cách gần đúng lực ma sát nghỉ cực đại bằng lực ma sát trượt. Góc α1 là
A. tan α1= 2µ.
B. tanα1=1/2μ
C. cosα1 = µ.
D. sinα1 = µ.
Phương pháp giải
- Áp dụng công thức tính lực ma sát nghỉ: Fmsn=μ.N
- Sử dụng các hệ thức lượng giác sin, cos, tan trong tam giác vuông để tính tana
Hướng dẫn giải
Gọi \(\vec Q\)là phản lực của tường tác dụng lên thanh tại đầu B. Gọi \(\vec R\) là phản lực của sàn nhà tác dụng lên thanh tại đầu A. Phản lực \(\vec R\)gồm phản lực pháp tuyến \(\vec N\)và phản lực tiếp tuyến (hình vẽ). Ta trượt các vecto trên giá của chúng đến điểm đồng quy O. Ta có:
\(\vec P + \vec Q + \vec R = \vec 0\)
- Từ hình vẽ ta có:
\(\begin{array}{l} \tan \theta = \frac{{{F_{msn}}}}{N} = \mu \\ \tan \theta = \frac{{AH}}{{OH}} = \frac{{L\cos {\alpha _1}}}{{2.L\sin {\alpha _1}}} = \frac{1}{{2\tan {\alpha _1}}} \end{array}\)
Suy ra:
\(\tan {\alpha _1} = \frac{1}{{2\mu }}\)
- Chọn đáp án B
4. Giải bài III.4 trang 52 SBT Vật lý 10
Một tấm ván đồng chất tiết diện đều, dài L được bắc qua một con mương. Bỏ qua độ dài của phần tấm ván tựa lên hai bờ mương. Một người có trọng lượng bằng trọng lượng P của tấm ván đứng trên tấm ván cách đầu A một đoạn là L/4. Hai bờ mương chịu các áp lực FA và FB lần lượt là
A. 5P/8
B. 3P/8; 5P/8
C. 3P/4; 5P/4
D. 5P/4; 3P/4
Phương pháp giải
Áp dụng qui tắc hợp lực song song cùng chiều:
\(\begin{array}{l} F_A^\prime + F_B^\prime = F_{AB}^\prime = 2P\\ \frac{{F_A^\prime }}{{F_B^\prime }} = \frac{{DB}}{{DA}} \end{array}\)
để tính các áp lực FA và FB
Hướng dẫn giải
Xem hình vẽ:
Gọi \(\overrightarrow {{P_{12}}} \) là hợp lực của trọng lực \(\vec P_1\) của ván và \(\vec P_2\) của người. Vì P1=P2=Pnên theo qui tắc hợp lực song song cùng chiều ta có:
P12=2P; CD=DG=L/8
- Theo qui tắc hợp lực song song cùng chiều, ta có:
\(\begin{array}{l} F_A^\prime + F_B^\prime = F_{AB}^\prime = 2P\\ \frac{{F_A^\prime }}{{F_B^\prime }} = \frac{{DB}}{{DA}} = \frac{{5L}}{8}:\frac{{3L}}{8} = \frac{5}{3} \end{array}\)
Suy ra F′A=5/4P và F′B=3/4P
- Theo định luật III Niuton, ván tác dụng lên hai bờ mương các áp lực:
FA=5/4P và FB=3/4P
- Chọn đáp án D
5. Giải bài III.5 trang 52 SBT Vật lý 10
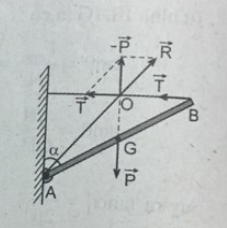
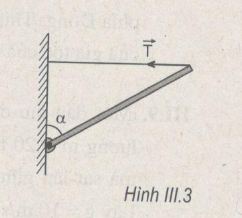
Một thanh đồng chất, tiết diện đều, một đầu được gắn với tường bằng một bản lề, đầu kia được giữ yên bằng một sợi dây nằm ngang (H.III.3). Cho biết góc α = 60° và lực căng của dây là T. Trọng lượng P của thanh và phản lực R của bản lề lần lượt là
\(\begin{array}{l} A.\,\,\frac{{T\sqrt 2 }}{3};T\sqrt {\frac{7}{3}} \\ B.\,\,2T\sqrt 3 ;T\sqrt {13} \\ C.\,\,\frac{T}{{\sqrt 3 }};\frac{{2T}}{{\sqrt 3 }}\\ D.\,\,\frac{{T\sqrt 2 }}{3};T \end{array}\)
Phương pháp giải
- Phân tích lực theo hình vẽ bên dưới
- Sử dụng các hệ thức lượng giác sin, cos, tan, cotg trong tam giác vuông để tìm trọng lượng P của thanh và phản lực R của bản lề
Hướng dẫn giải
- Xem hình vẽ:
\(\begin{array}{l} + \,\,\,P\frac{L}{2}\sin {60^0} = TL\cos {60^0}\\ + \,\,\,P = 2T\cot g{60^0} = \frac{{2T}}{{\sqrt 3 }}\\ + \,\,\,{R^2} = {P^2} + {T^2} = \frac{{4{T^2}}}{3} + {T^2}\\ \Rightarrow R = T\sqrt {\frac{7}{3}} \end{array}\)
- Chọn đáp án A
6. Giải bài III.6 trang 52 SBT Vật lý 10
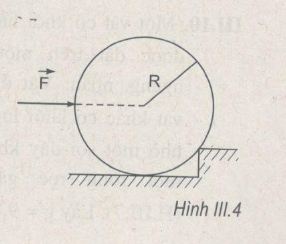
Để đẩy một con lăn nặng, bán kính R lên bậc thềm, người ta đặt vào nó một lực F theo phương ngang hướng đến trục (H.III.4). Lực này có độ lớn bằng trọng lượng của con lăn. Hãy xác định độ cao cực đại của bậc thềm.
Phương pháp giải
Xác định độ cao cực đại của bậc thềm theo công thức:
\(F(R - {h_m}) \ge P\sqrt {{R^2} - {{(R - {h_m})}^2}} \) và điều kiện: 0 < h < R
Hướng dẫn giải
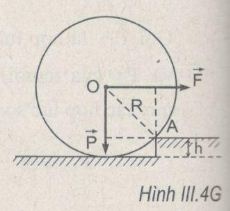
Con lăn vượt qua được bậc thềm nếu momen của lực \(\vec F\) đối với trục quay A lớn hơn hoặc bằng momen của trọng lực \(\vec P\) (H.III.4G)
- Ta có:
\(\begin{array}{l} F(R - h) \ge P\sqrt {{R^2} - {{(R - h)}^2}} \\ F(R - {h_m}) \ge P\sqrt {{R^2} - {{(R - {h_m})}^2}} \\ 2h_m^2 - 4R{h_m} + {R^2} = 0 \end{array}\)
- Vì chỉ lấy nghiệm 0 < h < R nên ta được hmax = 0,29R
7. Giải bài III.7 trang 52 SBT Vật lý 10
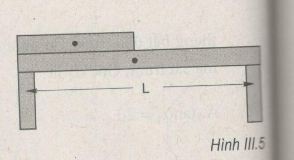
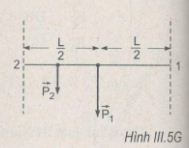
Một thanh dầm bằng thép có khối lượng 1 000 kg. Trên thanh dầm này có một thanh dầm khác giống hệt nhưng có chiều dài bằng một nửa (H.III.5). Hỏi mỗi cột đỡ chịu một lực bằng bao nhiêu ? Lấy g = 10 m/s2.
Phương pháp giải
- Áp dụng công thức: P=mg để tính trọng lượng cho mỗi cột
- Lập tỉ số hai giá trị trọng lượng vừa tìm được
- Tính áp lực theo công thức:
áp lực = trọng lượng đè lên cột 1 + trọng lượng đè lên cột 2
Hướng dẫn giải
- Ta phân tích lực \(\vec P_1\) thành hai lực tác dụng lên hai cột:
P11 = P12 = 0,5P1 = 0,5mg = 5000 N.
- Làm tương tự với \(\vec P_2\) ta được
P21 + P22 = P2 = 0,5mg
⇒ P21/P22=1/3
Suy ra :
P21=mg/8=10000/8=1250(N)
P22=3mg/8=3750(N)
- Áp lực lên cột 1 là:
F1 = P11 + P21 = 6250 N.
- Áp lực lên cột 2 là:
F2 = P12 + P22 = 8750 N.
8. Giải bài III.8 trang 53 SBT Vật lý 10
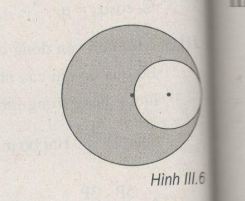
Người ta khoét một lỗ tròn bán kính R/2 trong một đĩa phẳng mỏng, đồng chất, bán kính R (H.III.6). Tìm trọng tâm của phần còn lại.
Phương pháp giải
- Lập tỉ số trọng lượng giữa hai phần với nhau:
GO/GO1=P1/P2
- Lỗ tròn nằm 1 phần bên hình tròn nên:
GO+GO1=R/2
- Giải hệ phương trình tìm trọng tâm của các phần
Hướng dẫn giải
Giả sử ta khoét thêm một lỗ tròn bán kính R/2 nữa đối xứng với lỗ tròn đã khoét lúc đầu (H.III.6G)
Gọi \(\vec P\) là trọng lượng của đĩa bán kính R khi chưa bị khoét, \(\vec P_1\) là trọng lượng của đĩa nhỏ có bán kính R/2 và \(\vec P_2\) là trọng lượng của phần đĩa còn lại sau hai lần khoét, ta có:
\(\begin{array}{l} \frac{{{P_1}}}{P} = \frac{{{S_1}}}{S} = \frac{{\frac{{\pi {R^2}}}{4}}}{{\pi {R^2}}} = \frac{1}{4}\\ \frac{{{P_2}}}{P} = \frac{{S - 2{S_1}}}{S} = \frac{{S - \frac{S}{2}}}{S} = \frac{1}{2}\\ \Rightarrow \frac{{{P_1}}}{{{P_2}}} = \frac{1}{2} \end{array}\)
Do tính chất đối xứng, trọng tâm phần đĩa còn lại sau hai lần khoét thì trùng với tâm O của đĩa khi chưa khoét, còn trọng tâm của đĩa nhỏ mà ta giả sử khoét thêm thì ở tâm O1 của nó. Gọi G là trọng tâm của đĩa sau khi bị khoét một lỗ tròn. Ta có hệ phương trình
- GO/GO1=P1/P2=1/2
- GO+GO1=R/2
Giải ra ta được: GO1=R/3 và GO=R/6
9. Giải bài III.9 trang 53 SBT Vật lý 10
Lực của gió tác dụng vào cánh buồm của một chiếc thuyền buồm là F1 = 380 N hướng về phía Bắc. Nước tác dụng vào thuyền một lực F2 = 190 N hướng về phía Đông. Thuyền có khối lượng tổng cộng là 270 kg. Hỏi độ lớn và hướng của gia tốc của thuyền ?
Phương pháp giải
- Áp dụng qui tắc tổng hợp lực: qui tắc hình bình hành
- Áp dụng định lí pytago để tính độ lớn của lực
- Áp dụng công thức: a=F/m để tính gia tốc
Hướng dẫn giải
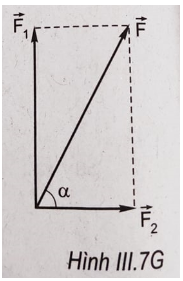
- Từ hình vẽ, ta có:
\(\begin{array}{l} + \,\,F = \sqrt {F_1^2 + F_2^2} = \sqrt {{{380}^2} + {{190}^2}} \\ = > F \approx 425N\\ + \,\,\tan \alpha = \frac{{{F_1}}}{{{F_2}}} = 2 = > \alpha = {63,5^0}\\ \end{array}\)
- Độ lớn gia tốc là:
\(a = \frac{F}{m} = \frac{{425}}{{270}} = 1,57(m/{s^2})\)
⇒ theo hướng Đông – Bắc
10. Giải bài III.10 trang 53 SBT Vật lý 10
Một đầu tàu có khối lượng M = 50 tấn được nối với một toa xe có khối lượng m = 20 tấn. Đoàn tàu bắt đầu rời ga với gia tốc a = 0,2 m/s2. Bỏ qua ma sát lăn giữa bánh xe và mặt đường ray và khối lượng của các bánh xe. Lấy g = 10 m/s2.
a) Tính lực phát động của đầu tàu.
b) Tính lực căng ở chỗ nối.
c) Lực nào là lực kéo của đầu tàu ?
Phương pháp giải
a. Áp dụng công thức:
Fpd = (M + m)a để tính lực phát động
b. Tính lực căng theo công thức: T= ma
c. Lực kéo của tàu bằng lực căng T
Hướng dẫn giải
a. Chọn trục Ox theo chiều chuyển động.
Lực phát động là lực ma sát nghỉ từ phía mặt đường tác dụng lên các bánh xe phát động của đầu tàu. Lực này hướng về phía trước, gây ra gia tốc cho cả đoàn tàu.
Fpd = (M + m)a = (50000 + 20000).0,2 = 14000 N.
b. Xét riêng toa xe:
T = ma = 20000.0,2 = 4000 N.
c. Đầu tàu kéo toa xe bằng một lực, gọi là lực kéo của đầu tàu (ở đây là lực căng T2)
Fk = 4000 N.
11. Giải bài III.11 trang 53 SBT Vật lý 10
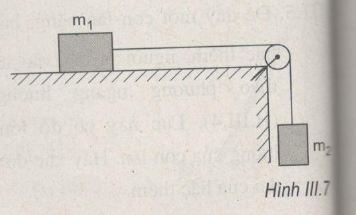
Một vật có khối lượng m1 =3,0 kg được đặt trên một mặt bàn nằm ngang, nhẵn. Vật được nối với một vật khác có khối lượng m2 = 1,0 kg nhờ một sợi dây không dãn vắt qua một ròng rọc gắn ở mép bàn (H.III.7). Lấy g = 9,8 m/s2.
a) Tính gia tốc của mỗi vật.
b) Nếu lúc đầu vật m1 đứng yên cách mép bàn 150 cm thì sau bao lâu sau nó sẽ đến mép bàn.
c) Tính lực căng của dây.
Phương pháp giải
a) Vận dụng lí thuyết của định luật III Niuton: Trong mọi trường hợp, khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng lại vật A một lực. Hai lực này có cùng giá, cùng độ lớn, nhưng ngược chiều.
Áp dụng định luật II Niuton: F = m.a để tính gia tốc
b) Thời gian dịch chuyển được tính theo công thức:
\(t = \sqrt {\frac{{2s}}{a}} \)
c) Tính lực căng của dây theo công thức:
T = m2(g – a)
Hướng dẫn giải
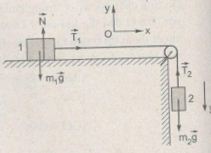
Chọn chiều dương là chiều chuyển động của dây (H.III.8G)
a. Xét vật 1: Oy: N – m1g = 0; Ox: a=T1/m1 (1)
Xét vật 2: Oy: m2a = m2g – T2 (2)
- Theo định luật III Niu-tơn:
T1 = T2 = T (3)
- Từ (1), (2) và (3) suy ra
\(\begin{array}{l} a = \frac{{{m_2}g}}{{{m_1} + {m_2}}}\\ = \frac{{1,0.9,8}}{{3,0 + 1,0}} = 2,45 \approx 2,5(m/{s^2}) \end{array}\)
b. Thời gian đến mép bàn là:
\(\begin{array}{l} s = \frac{1}{2}a{t^2}\\ = > t = \sqrt {\frac{{2s}}{a}} = \sqrt {\frac{{2.1,50}}{{2,45}}} = 1,1(s) \end{array}\)
c. Từ (2) và (3)
T = m2(g – a) = 1,0(9,8 – 2,45) = 7,35 N
12. Giải bài III.12 trang 54 SBT Vật lý 10
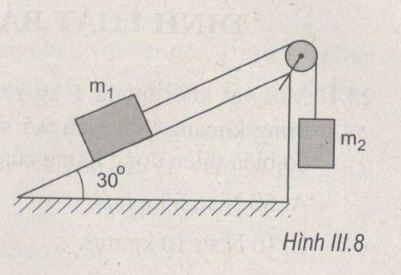
Một vật có khối lượng m1 =3,7 kg nằm trên một mặt không ma sát, nghiêng 30° so với phương ngang. Vật được nối với một vật thứ hai có khối lượng m2 = 2,3 kg bằng một sợi dây không dãn vắt qua một ròng rọc gắn ở đỉnh của mặt phẳng nghiêng (H.III.8).Cho g = 9,8 m/s2.
a) Tính gia tốc và hướng chuyển động của mỗi vật.
b) Tính lực căng của dây.
Phương pháp giải
a) Phân tích lực cho hai vật theo hai thành phần Ox và Oy để tìm dấu của gia tốc a
b) Tính lực căng dây theo công thức:
T = m2(g – a)
Hướng dẫn giải
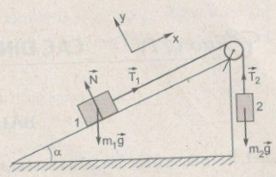
a. Chọn chiều dương của hệ tọa độ cho mỗi vật như hình vẽ
-Xét vật 1: Oy: N – m1gcosα = 0; Ox: T1 – m1gsinα = m1a (1)
- Xét vật 2: m2g – T2 = m2a (2); T1 = T2 = T (3)
- Từ (1), (2) và (3) suy ra:
a > 0: vật m2 đi xuống và vật m1 đi lên.
b. Từ (2) và (3) suy ra:
T = m2(g – a) = 2,30(9,8 – 0,735) = 20,84 N.
Tham khảo thêm
- doc Giải bài tập SBT Vật Lí 10 Bài 17: Cân bằng của một vật chịu tác dụng của hai lực và của ba lực không song song
- doc Giải bài tập SBT Vật Lí 10 Bài 18: Cân bằng của một vật có trục quay cố định. Momen lực
- doc Giải bài tập SBT Vật Lí 10 Bài 19: Quy tắc hợp lực song song cùng chiều
- doc Giải bài tập SBT Vật Lí 10 Bài 20: Các dạng cân bằng. Cân bằng của một vật có mặt chân đế
- doc Giải bài tập SBT Vật Lí 10 Bài 21: Chuyển động tịnh tiến của vật rắn. Chuyển động quay của vật rắn quanh một trục cố định
- doc Giải bài tập SBT Vật Lí 10 Bài 22: Ngẫu lực