Giải bài tập SBT Vật Lí 10 Bài tập cuối chương I: Động học chất điểm

1. Giải bài I.1 trang 20 SBT Vật lý 10

Một ô tô chạy từ tỉnh A đến tỉnh B. Trong nửa đoạn đường đầu, xe chuyển động với tốc độ 40 km/h. Trong nửa đoạn đường sau, xe chuyển động với tốc độ 60 km/h. Hỏi tốc độ trung bình vtb của ô tô trên đoạn đường AB bằng bao nhiêu ?

A. 24 km/h.         B. 48 km/h.

C. 50 km/h.         D. 40 km/h.

Phương pháp giải

Hướng dẫn giải

Gọi quãng đường AB là S (km, S > 0)

- Trong nửa đoạn đường đầu, xe chuyển động với tốc độ 40 km/h, suy ra thời gian xe đi nửa đoạn đường đầu là:

\({t_1} = \frac{{S/2}}{{40}} = \frac{S}{{80}}(h)\)

- Trong nửa đoạn đường sau, xe chuyển động với tốc độ 60 km/h, suy ra thời gian xe đi nửa đoạn đường sau là:

\({t_2} = \frac{{S/2}}{{60}} = \frac{S}{{120}}(h)\)

- Tổng thời gian xe chuyển động là:

\(t = {t_1} + {t_2} = \frac{S}{{80}} + \frac{S}{{120}} = \frac{S}{{48}}(h)\)

- Vậy tốc độ trung bình của ô tô là: 

\(v = \frac{S}{t} = \frac{S}{{S/48}} = 48(km/h)\)

- Chọn đáp án B

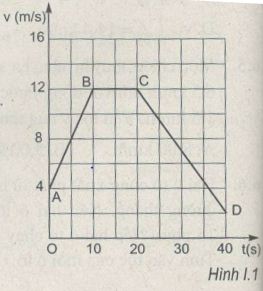
Hình 1.1 là đồ thị vận tốc - thời gian của một vật chuyển động thẳng. Theo đồ thị này, gia tốc a của vật tương ứng với các đoạn AB, BC, CD là bao nhiêu ?

A. Đoạn AB : a₁ = 0,8 m/s²                

    Đoạn BC : a₂ = 0.

    Đoạn CD : a₃ = 0,5 m/s².

B. Đoạn AB :  a₁ = 1,8 m/s².

    Đoạn BC : a₂ = 0.

    Đoạn CD : a₃ = - 0,5 m/s².

C. Đoạn AB :  a₁ = 0,8 m/s² .      

    Đoạn BC : a₂ = 0.    

    Đoạn CD : a₃ = -1 m/s².

D. Đoạn AB :  a₁ = 0,8 m/s² .

    Đoạn BC : a₂ = 0.

    Đoạn CD : a₃ = -0,5 m/s².

Phương pháp giải

Áp dụng công thức:

\(a = \frac{{v - {v_0}}}{t}\) tính gia tốc cho từng quá trình

Hướng dẫn giải

- Gia tốc trên từng quá trình là:

AB: \({a_1} = \frac{{12 - 4}}{{10}} = 0,8(m/{s^2})\)$$

BC: \({a_2} = 0(m/{s^2})\)$$

CD: \({a_3} = \frac{{2 - 12}}{{40 - 20}} = - 0,5(m/{s^2})\)$$

- Chọn đáp án D

Một ô tô chuyển động thẳng nhanh dần đều. Sau 10 s, vận tốc của ô tô tăng từ 4 m/s đến 6 m/s. Quãng đường s mà ô tô đã đi được trong khoảng thời gian này là bao nhiêu ?

A. 100 m.               B. 50 m.

C. 25 m.                 D. 500 m.

Phương pháp giải

- Áp dụng công thức:

\(a = \frac{{v - {v_0}}}{t}\) để tính gia tốc

- Áp dụng công thức:

\(S = \frac{{{v^2} - v_0^2}}{{2a}}\) để tính quãng đường

Hướng dẫn giải

- Gia tốc chuyển động là:

\(\begin{array}{l} v = {v_0} + at\\ \Rightarrow a = \frac{{v - {v_0}}}{t} = \frac{{6 - 4}}{{10}} = 0,2 \end{array}\)

- Quãng đường s mà ô tô đã đi được là:

\(\begin{array}{l} {v^2} - v_0^2 = 2aS\\ \Rightarrow S = \frac{{{v^2} - v_0^2}}{{2a}} = \frac{{{6^2} - {4^2}}}{{2.0,2}} = 50(m) \end{array}\)

- Chọn đáp án B

Một xe lửa bắt đầu rời khỏi ga và chuyển động thẳng nhanh dần đều với gia tốc 0,1 m/s². Khoảng thời gian t để xe lửa đạt được vận tốc 36 km/h là bao nhiêu ?

A. 360 s.                 B. 200 s.

C. 300 s.                 D. 100 s.

Phương pháp giải

Tính thời gian theo công thức:

\(t = \frac{{v - {v_0}}}{a}\)

Hướng dẫn giải

- Khoảng thời gian t để xe lửa đạt được vận tốc 36 km/h là

\(\begin{array}{l} v = {v_0} + at\\ \Rightarrow t = \frac{{v - {v_0}}}{a} = \frac{{10 - 0}}{{0,1}} = 100s \end{array}\)

- Chọn đáp án D

Một ô tô đang chuyển động với vận tốc 54 km/h thì người lái xe hãm phanh. Ô tô chuyển động thẳng chậm dần đều và sau 6 giây thì dừng lại. Quãng đường s mà ô tô đã chạy thêm được kể từ lúc hãm phanh là bao nhiêu ?

A. s = 45 m.           B. s = 82,6 m.      

C. s = 252m.          D. s = 135 m.

Phương pháp giải

- Áp dụng công thức:

\(a = \frac{{v - {v_0}}}{t}\) để tính gia tốc

- Áp dụng công thức:

\(S = \frac{{{v^2} - v_0^2}}{{2a}}\) để tính quãng đường

Hướng dẫn giải

- Gia tốc chuyển động là:

\(a = \frac{{v - {v_0}}}{t} = \frac{{0 - 15}}{6} = - 2,5(m/{s^2})\)

- Quãng đường s mà ô tô đã chạy thêm được kể từ lúc hãm phanh là:

\(S = \frac{{{v^2} - v_0^2}}{{2a}} = \frac{{{0^2} - {{15}^2}}}{{2.( - 2,5)}} = 45(m)\)

- Chọn đáp án A

Nếu lấy gia tốc rơi tự do là g = 10 m/s² thì tốc độ trung bình v_tb của một vật trong chuyển động rơi tự do từ độ cao 20 m xuống tới đất sẽ là bao nhiêu ?

A. v_tb = 15 m/s.                   B. v_tb = 8 m/s.

C. v_tb = 10 m/s.                   D. v_tb = 1 m/s

Phương pháp giải

- Áp dụng công thức:

\(t = \sqrt {\frac{{2h}}{g}} \) để tính thời gian rơi

- Tính tốc độ trung bình theo công thức:

\({v_{tb}} = \frac{S}{t}\)

Hướng dẫn giải

- Thời gian vật rơi là:

\(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.20}}{{10}}} = 2(s)\)

- Vận tốc trung bình là:

\({v_{tb}} = \frac{S}{t} = \frac{{20}}{2} = 10(m/s)\)

- Chọn đáp án C

Một đĩa tròn bán kính 20 cm quay đều quanh trục của nó. Đĩa quay 1 vòng hết đúng 0,2 s. Hỏi tốc độ dài v của một điểm nằm trên mép đĩa bằng bao nhiêu ?

A. v = 62,8 m/s.                 B. v = 3,14 m/s.

C. v = 628 m/s.                  D. v = 6,28 m/s.

Phương pháp giải

Tính vận tốc dài theo công thức:

 v=ω.r với ω=2π/T

Hướng dẫn giải

- Vận tốc góc là: 

ω=2π/T=2π/0,2=10π(rad/s)

- Vận tốc dài là:

 v=ω.r=10π.0,2=6,28(m/s)

- Chọn đáp án D

Hai bến sông A và B cùng nằm trên một bờ sông, cách nhau 18 km. Cho biết vận tốc của ca nô đối với nước là 16,2 km/h và vận tốc của nước đối với bờ sông là 5,4 km/h. Hỏi khoảng thời gian t để một ca nô chạy xuôi dòng từ A đến B rồi lại chạy ngược dòng trở về A bằng bao nhiêu ?

A. t = 1 giờ 40 phút.

B. t ≈ 1 giờ 20 phút.

C. t = 2 giờ 30 phút.

D. t = 2 giờ 10 phút.

Phương pháp giải

- Áp dụng công thức cộng vận tốc:

\(\overrightarrow {{v_{thuyen - bo}}} = \overrightarrow {{v_{thuyen - nuoc}}} + \overrightarrow {{v_{nuoc - bo}}} \)

+ Tính vận tốc thuyền khi đi xuôi dòng:

\(\begin{array}{l} {v_{thuyen - bo}} = {v_{thuyen - nuoc}} + {v_{nuoc - bo}}\\ \end{array}\)

+ Tính vận tốc thuyền khi đi ngược dòng:

\(\begin{array}{l} {v_{thuyen - bo}} = {v_{thuyen - nuoc}} - {v_{nuoc - bo}}\\ \end{array}\)

- Áp dụng công thức: t=s/v để tính thời gian

Hướng dẫn giải

Ta có: 

\(\overrightarrow {{v_{thuyen - bo}}} = \overrightarrow {{v_{thuyen - nuoc}}} + \overrightarrow {{v_{nuoc - bo}}} \)

Chọn chiều dương cùng chiều chuyển động của thuyền

- Khi thuyền đi xuôi dòng:

\(\begin{array}{l} {v_{thuyen - bo}} = {v_{thuyen - nuoc}} + {v_{nuoc - bo}}\\ = 16,2 + 5,4 = 21,6(km/h) = {v_1} \end{array}\)

- Thời gian khi thuyền đi xuôi dòng là:

\({t_1} = \frac{S}{{{v_1}}} = \frac{{18}}{{21,6}} = \frac{5}{6}(h)\)

- Khi thuyền đi ngược dòng: 

\(\begin{array}{l} {v_{thuyen - bo}} = {v_{thuyen - nuoc}} - {v_{nuoc - bo}}\\ = 16,2 - 5,4 = 10,8(km/h) \end{array}\)

- Thời gian khi thuyền đi ngược dòng là: 

\({t_2} = \frac{S}{{{v_2}}} = \frac{{18}}{{10,8}} = \frac{5}{3}(h)\)

Vậy tổng thời gian thuyền đi và về là:

 t=t₁+t₂=56+53=2,5(h)

- Chọn đáp án C

Một ô tô và một xe máy xuất phát cùng một lúc từ hai địa điểm A và B cách nhau 20 km và chuyển động thẳng đều theo chiều từ A đến B. Ô tô đi từ A có vận tốc là 80 km/h và xe máy đi từ B có vận tốc là 40 km/h. Chọn A làm gốc toạ độ, chiều từ A đến B là chiều dương và chọn thời điểm xuất phát của hai xe làm mốc thời gian.

a) Viết phương trình chuyển động của mỗi xe.

b) Tính thời điểm và vị trí hai xe đuổi kịp nhau.

c) Vẽ đồ thị toạ độ - thời gian của hai xe. Căn cứ vào đồ thị này, hãy xác định vị trí và thời điểm hai xe đuổi kịp nhau. So sánh kết quả tìm được trên đồ thị với kết quả tính trong câu b).

Phương pháp giải

a) Viết phương trình dưới dạng: x=v.t

b) Khi hai xe gặp nhau: x_A = x_B 

⇒ giải phương trình tìm thời điểm gặp nhau t, thay t vào phương trình x_A để tìm vị trí\

c) Vận dụng lí thuyết về chuyển động thẳng để vẽ đồ thị

Hướng dẫn giải

a) Phương trình chuyển động của ô tô : x_A = 80t

Phương trình chuyển động của xe máy : x_B = 20 + 40t

b) Hai xe gặp nhau khi x_A = x_B. Từ đó suy ra:

- Thời điểm hai xe gặp nhau kể từ khi xuất phát:

80t = 20 + 40t
Hay t=20/40=0,5(h)

- Vị trí hai xe gặp nhau cách A một đoạn: x_A = 80.0,5 = 40 km.

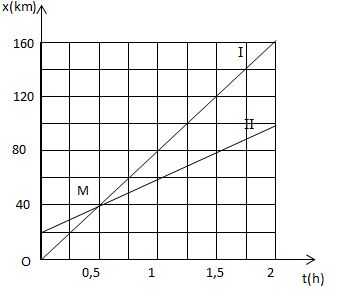
c) Đồ thị toạ độ của hai xe có dạng như  trên hình I.1G, trong đó đường I biểu diễn chuyển động của ô tô và đường II biểu diễn chuyển động của xe máy.

Căn cứ vào đồ thị trên hình I.l G, ta thấy hai đường biểu diễn I và II giao nhau tại điểm M ứng với thời điểm hai  xe gặp nhau t = 0,5 giờ = 30 phút ở vị trí có toạ độ x = 40 km.

Như vậy kết quả tìm được trên đồ thị trùng với kết quả tính toán trong câu b).

Một ô tô chuyển động thẳng nhanh dần đều đi qua điểm A rồi qua điểm B cách A 20 m trong thời gian t = 2 s. Vận tốc của ô tô khi đi qua điểm B là v_B= 12 m/s.

a) Tính gia tốc của ô tô và vận tốc của nó khi đi qua điểm A.

b) Tính quãng đường ô tô đã đi được từ điểm khởi hành đến điểm A.

Phương pháp giải

a)- Tính gia tốc của ô tô theo công thức:

 a=v_B−v_At

Tính vận tốc theo công thức:

\({v_A} = \frac{{2s}}{t} - {v_B}\)

b) Tính quãng đường ô tô đã đi được theo công thức:

\(\begin{array}{l} {s_A} = \frac{{at_A^2}}{2}\\ \end{array}\)

Hướng dẫn giải

Chọn thời điểm ô tô đi qua điểm A làm mốc thời gian. Vì ô tô chuyển động thẳng nhanh dần đều nên gia tốc của ô tô được tính theo công thức: a=v_B−v_At(1)

Mặt khác gia tốc a lại liên hệ với quãng đường đi được s và các vận tốc v_A và v_B theo công thức: v²_B−v²_A=2as

a) Ta suy ra 2s = (v_B + v_A)t

hay  \({v_A} = \frac{{2s}}{t} - {v_B} = \frac{{2.20}}{2} - 12 = 8(m/s)\)

Thay số vào (1) ta tính được gia tốc của ô tô:  

\(a = \frac{{12 - 8}}{2} = 2(m/{s^2})\)

b) Vì vận tốc đầu v₀ = 0, nên quãng đường đi được của ô tô kể từ điểm khởi hành cho đến điểm A tính bằng: \(\begin{array}{l} {s_A} = \frac{{at_A^2}}{2}\\ \end{array}\)

Vì v_A = a.t_A nên suy ra: 

\(\begin{array}{l} {s_A} = \frac{{at_A^2}}{2}\\ = \frac{a}{2}{\left( {\frac{{{v_A}}}{a}} \right)^2} = \frac{{v_A^2}}{{2a}} = \frac{{{8^2}}}{{2.2}} = 16(m) \end{array}\)

Một xe đạp đang đi với vận tốc 12 km/h thì hãm phanh. Xe chuyển động chậm dần đều và đi được thêm 10 m thì dừng lại.

a) Tính gia tốc của xe.

b) Tính thời gian hãm phanh.

Phương pháp giải

a) Tính gia tốc của xe theo công thức:

v² – v₀² = 2as thay số và tìm a

b) Tính thời gian hãm phanh theo công thức:

v = v₀ + at thay số và tìm t

Hướng dẫn giải

a) Vận tốc xe đạp trước khi hãm phanh : v₀ = 12 km/h = 10/3 (m/s)

Áp dụng công thức giữa vận tốc, gia tốc và quãng đường đi được: 

v² – v₀² = 2as với v = 0 và s = 10 m ;

ta tính được a = - 5/9  ≈ - 0,55 m/s².

Vậy, gia tốc của xe đạp là - 0,55 m/s².

b)  Áp dụng công thức tính vận tốc v = v₀ + at

ta tính được : t = 90/15 = 6 s.

Vậy, thời gian hãm phanh là 6 giây.

Một hòn bi lăn xuống một máng nghiêng theo đường thẳng. Khoảng cách giữa 5 vị trí liên tiếp A, B, C, D, E của hòn bi là AB = 3 cm, BC = 4 cm, CD = 5cm và DE = 6 cm. Khoảng thời gian để hòn bi lăn trên các đoạn AB, BC, CD và DE đều là 0,5 s.

a) Chứng minh chuyển động của hòn bi là chuyển động thẳng, nhanh dần đều.

b) Tính gia tốc của hòn bi.

Phương pháp giải

a) Mỗi đoạn thẳng tương ứng với mỗi quãng đường hòn bi chuyển động được

- Áp dụng công thức:

\(s = \frac{1}{2}a{t^2}\) để tính quãng đường hay độ dài mỗi đoạn thẳng

- Rút gọn các phương trình trên bằng phép trừ, ta được:

l₂ – l₁ = aΔt₂;  l₃ – l₂ = = aΔt₂; l₄ – l₃ = = aΔt₂

⇒ kết quả này chứng tỏ chuyển động của hòn bi là chuyển động thẳng, nhanh dần đều

b) Tính gia tốc của hòn bi theo công thức:

a=l₂−l₁Δt₂

Hướng dẫn giải

a) Giả sử hòn bi chuyển động thẳng nhanh dần đều. Ta hãy tìm quy luật biến đổi của những quãng đường đi được liên tiếp trong những khoảng thời gian bằng nhau.

- Đặt l₁ = AB ; l₂ = BC ; l₃ = CD ; l₄ = DE.

- Gọi Δt là những khoảng thời gian bằng nhau liên tiếp mà hòn bi chuyển động trên các đoạn đường AB, BC, CD và DE.

- Giả sử hòn bi xuất phát không vận tốc đầu từ điểm O và sau khoảng thời gian t nó lăn đến điểm A.

- Gọi a là gia tốc của hòn bi, ta có:

\(\begin{array}{l} OA = \frac{1}{2}a{t^2}(1)\\ OB = \frac{1}{2}a{(t + {\rm{\Delta }}t)^2} = s + AB(2)\\ OC = \frac{1}{2}a{(t + 2{\rm{\Delta }}t)^2} = s + AB + BC\\ = s + AB + BC + CD(3)\\ OD = \frac{1}{2}a{(t + 3{\rm{\Delta }}t)^2}\\ = s + AB + BC + CD(4)\\ OE = \frac{1}{2}a{(t + 4{\rm{\Delta }}t)^2}\\ = s + AB + BC + CD + DE(5) \end{array}\)

- Lần lượt làm các phép trừ vế với vế các phương trình trên, ta có :

(2) - (1):  \(AB = at{\rm{\Delta }}t + \frac{1}{2}a{\rm{\Delta }}{t^2} = {l_1}\)

(3) - (2): \(BC = at{\rm{\Delta }}t + \frac{3}{2}a{\rm{\Delta }}{t^2} = {l_2}\)

(4) - (3): \(CD = at{\rm{\Delta }}t + \frac{5}{2}a{\rm{\Delta }}{t^2} = {l_3}\)

(5) - (4): \(DE = at{\rm{\Delta }}t + \frac{7}{2}a{\rm{\Delta }}{t^2} = {l_4}\)

- Từ các kết quả trên, ta rút ra nhận xét sau :

l₂ – l₁ = aΔt₂;  l₃ – l₂ = = aΔt₂; l₄ – l₃ = = aΔt₂

Vậy, trong chuyển động thẳng nhanh dần đều, hiệu những quãng đường đi được trong hai khoảng thời gian liên tiếp bằng nhau là một lượng không đổi.

- Áp dụng vào bài toán này (AB = 3 cm, BC = 4 cm, CD = 5 cm và DE = 6 cm) ta thấy :

BC - AB = CD - BC = DE - CD = 1 cm

Vậy, chuyển động của hòn bi là chuyển động thẳng nhanh dần đều.

b) Từ phép tính trên ta rút ra công thức tính gia tốc của hòn bi là: 

a=l₂−l₁Δt₂

Với l₂ – l₁ = 1 cm ; Δt = 0,5 s ;

ta có a = 4.10^-2m/s² = 4 cm/s².

Nếu có một giọt nước mưa rơi được 100 m trong giây cuối cùng trước khi chạm đất, thì giọt nước mưa đó phải bắt đầu rơi từ độ cao bao nhiêu mét ? Cho rằng chuyển động của giọt nước mưa là rơi tự do với g = 9,8 m/s² và trong suốt quá trình rơi, khối lượng của nó không bị thay đổi.

Phương pháp giải

- Giải phương trình quãng đường rơi của giọt nước:

s+100=1/2g(t+1)² để tìm thời gian t

- Thay giá trị t vừa tìm được và phương trình tính quãng đường:

s=1/2gt² để tìm độ cao: h= s +100

Hướng dẫn giải

Gọi s là quãng đường rơi của giọt nước mưa từ lúc đầu đến điểm cách mặt đất 100 m, t là thời gian rơi trên quãng đường đó, ta có: s=1/2gt²(1)

- Mặt khác, quãng đường rơi từ lúc đầu đến mặt đất là s + 100 và thời gian rơi trên quãng đường đó là t + 1 giây.

- Ta có :s+100=1/2g(t+1)² (2)

- Từ hai phương trình (1) và (2) ta rút ra: 

\(t = \frac{{100}}{9} - 0,5 \approx 9,7(s) = > s = 461(m)\)

Vậy, độ cao ban đầu của giọt nước mưa lúc bắt đầu rơi là: 

h= s +100 = 561 m.