Giải bài tập SBT Vật Lí 10 Bài 3: Chuyển động thẳng biến đổi đều
Mời các em học sinh cùng tham khảo nội dung giải Bài 3 SBT Vật Lý 10 dưới đây. Hy vọng đây sẽ là tài liệu hữu ích giúp các em rèn luyện phương pháp giải bài tập về: Chuyển động thẳng biến đổi đều.
Mục lục nội dung
1. Giải bài 3.1 trang 11 SBT Vật lý 10
2. Giải bài 3.2 trang 11 SBT Vật lý 10
3. Giải bài 3.3 trang 11 SBT Vật lý 10
4. Giải bài 3.4 trang 12 SBT Vật lý 10
5. Giải bài 3.4 trang 12 SBT Vật lý 10
6. Giải bài 3.6 trang 12 SBT Vật lý 10
7. Giải bài 3.7 trang 12 SBT Vật lý 10
8. Giải bài 3.8 trang 13 SBT Vật lý 10
9. Giải bài 3.9 trang 13 SBT Vật lý 10
10. Giải bài 3.10 trang 13 SBT Vật lý 10
11. Giải bài 3.11 trang 13 SBT Vật lý 10
12. Giải bài 3.12 trang 13 SBT Vật lý 10
13. Giải bài 3.13 trang 13 SBT Vật lý 10
14. Giải bài 3.14 trang 13 SBT Vật lý 10
15. Giải bài 3.15 trang 14 SBT Vật lý 10
16. Giải bài 3.16 trang 14 SBT Vật lý 10

1. Giải bài 3.1 trang 11 SBT Vật lý 10
Câu nào sai ?
Trong chuyển động thẳng nhanh dần đều thì
A. vectơ gia tốc ngược chiều với vectơ vận tốc.
B. vận tốc tức thời tăng theo hàm số bậc nhất của thời gian.
C. quãng đường đi được tăng theo hàm số bậc hai của thời gian.
D. gia tốc là đại lượng không đổi.
Phương pháp giải
Để trả lời câu hỏi này cần nắm được các đặc điểm của chuyển động thẳng nhanh dần đều
Hướng dẫn giải
- Vectơ gia tốc ngược chiều với vectơ vận tốc. → A sai
- Chọn đáp án A
2. Giải bài 3.2 trang 11 SBT Vật lý 10
Chỉ ra câu sai.
A. Vận tốc tức thời của chuyển động thẳng biến đổi đều có độ lớn tăng hoặc giảm đều theo thời gian.
B. Gia tốc của chuyển động thẳng biến đổi đều có độ lớn không đổi.
C. Vectơ gia tốc của chuyển động thẳng biến đổi đều có thể cùng chiều hoặc ngược chiều với vectơ vận tốc.
D. Trong chuyển động thẳng biến đổi đều, quãng đường đi được trong những khoảng thời gian bằng nhau thì bằng nhau.
Phương pháp giải
Quãng đường vật đi được trong chuyển động thẳng biến đổi đều tủy thuộc vào gia tốc của vật
Hướng dẫn giải
- Trong chuyển động thẳng biến đổi đều, quãng đường đi được trong những khoảng thời gian bằng nhau thì bằng nhau → D sai
- Chọn đáp án D
3. Giải bài 3.3 trang 11 SBT Vật lý 10
Câu nào đúng ?
Công thức tính quãng đường đi được của chuyển động thẳng nhanh dần đều là
A. \(s = {v_0}t + \frac{{a{t^2}}}{2} \) (a và v0 cùng dấu)
B. \(s = {v_0}t + \frac{{a{t^2}}}{2}\) (a và v0 trái dấu)
C. \(x = {x_0} + {v_0}t + \frac{{a{t^2}}}{2}\) (a và v0 cùng dấu)
D. \(x = {x_0} + {v_0}t + \frac{{a{t^2}}}{2}\) (a và v0 trái dấu)
Phương pháp giải
Quãng đường trong chuyển động thẳng nhanh dần đều tính theo công thức:
\(s = {v_0}t + \frac{{a{t^2}}}{2} \)(a và v0 cùng dấu)
Hướng dẫn giải
- Công thức tính quãng đường đi được của chuyển động thẳng nhanh dần đều là:
\(s = {v_0}t + \frac{{a{t^2}}}{2} \) (a và v0 cùng dấu)
- Chọn đáp án A
4. Giải bài 3.4 trang 12 SBT Vật lý 10
Câu nào đúng ?
Phương trình chuyển động của chuyển động thẳng chậm dần đều là:
A. \(s = {v_0}t + \frac{{a{t^2}}}{2}\) (a và v0 cùng dấu)
B. \(s = {v_0}t + \frac{{a{t^2}}}{2}\) (a và v0 trái dấu)
C. \(x = {x_0} + {v_0}t + \frac{{a{t^2}}}{2}\) (a và v0 cùng dấu)
D. \(x = {x_0} + {v_0}t + \frac{{a{t^2}}}{2}\) (a và v0 trái dấu)
Phương pháp giải
Phương trình trong chuyển động thẳng chậm dần đều:
\(x = {x_0} + {v_0}t + \frac{{a{t^2}}}{2}\)(a và v0 trái dấu)
Hướng dẫn giải
- Phương trình chuyển động của chuyển động thẳng chậm dần đều là:
\(x = {x_0} + {v_0}t + \frac{{a{t^2}}}{2}\) (a và v0 trái dấu)
- Chọn đáp án D
5. Giải bài 3.5 trang 12 SBT Vật lý 10
Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động thẳng nhanh dần đều (v2 – v02 = 2as), ta có các điều kiện nào dưới đây ?
A. s > 0 ; a > 0 ; v > v0. B. s > 0 ; a < 0 ; v < v0.
C. s > 0 ; a > 0 ; v < v0. D. s > 0 ; a < 0 ; v > v0.
Phương pháp giải
Trong chuyển động thẳng nhanh dần đều có: s > 0 ; a > 0 ; v > v0
Hướng dẫn giải
- Điều kiện: s > 0 ; a > 0 ; v > v0
- Chọn đáp án A
6. Giải bài 3.6 trang 12 SBT Vật lý 10
Hình 3.1 là đồ thị vận tốc theo thời gian của một xe máy chuyển động trên một đường thẳng. Trong khoảng thời gian nào, xe máy chuyển động chậm dần đều ?
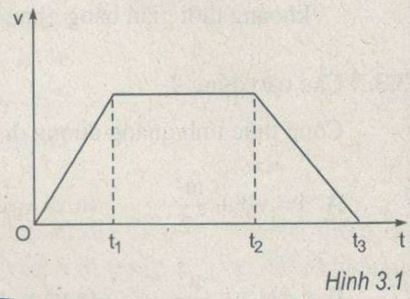
A. Trong khoảng thời gian từ 0 đến t1 .
B. Trong khoảng thời gian từ t1 đến t2 .
C. Trong khoảng thời gian từ t2 đến t3 .
D. Các câu trả lời A, B, C đều sai.
Phương pháp giải
Dựa vào hình vẽ để xác định tính chất chuyển động của từng đoạn
Hướng dẫn giải
- Trong khoảng thời gian từ t2 đến t3 , xe máy chuyển động chậm dần đều.
- Chọn đáp án C
7. Giải bài 3.7 trang 12 SBT Vật lý 10
Khi ô tô đang chạy với vận tốc 10 m/s trên đoạn đường thẳng thì người lái xe tăng ga và ô tô chuyển động nhanh dần đều. Sau 20 s, ô tô đạt vận tốc 14 m/s. Gia tốc a và vận tốc v của ô tô sau 40 s kể từ lúc bắt đầu tăng ga là bao nhiêu ?
A. a = 0,7 m/s2 ; v = 38 m/s. B. a = 0,2 m/s2 ; v = 18 m/s.
C. a = 0,2 m/s2 ; v = 8 m/s. D. a = 1,4 m/s2 ; v = 66 m/s.
Phương pháp giải
- Áp dụng công thức:
\(a = \frac{{v - {v_0}}}{t}\) để tính gia tốc
- Vận tốc tính theo công thức: \(v = 10 + 0,2t\)
Hướng dẫn giải
- Ta có:
\(v = {v_0} + at \Rightarrow a = \frac{{v - {v_0}}}{t}\)
- Thay số vào ta được:
+ Gia tốc vật là: a = 0,2 m/s2
+ Vận tốc v của ô tô sau 40 s kể từ lúc bắt đầu tăng ga là:
\(v = 10 + 0,2t\) = 18 m/s
- Chọn đáp án B
8. Giải bài 3.8 trang 13 SBT Vật lý 10
Cũng bài toán trên, hỏi quãng đường s mà ô tô đã đi được sau 40 s kể từ lúc bắt đầu tăng ga và tốc độ trung bìnhvtb trên quãng đường đó là bao nhiêu ?
A. s = 480 m ; vtb = 12 m/s. B. s = 360 m ; vtb = 9 m/s.
C. s = 160 m ; vtb = 4 m/s. D. s = 560 m ; vtb = 14 m/s.
Phương pháp giải
- Áp dụng công thức:
\(S = \frac{{{v^2} - v_0^2}}{{2a}}\) để tính quãng đường
- Vận tốc trung bình tính theo công thức: vtb=S/t
Hướng dẫn giải
- Quãng đường mà người đó đã đi được sau 40s40s là:
\(\begin{array}{l} {v^2} - v_0^2 = 2aS\\ \Rightarrow S = \frac{{{v^2} - v_0^2}}{{2a}} = \frac{{{{18}^2} - {{10}^2}}}{{2.0,2}} = 560(m) \end{array}\)
- Vận tốc trung bình của người đó là:
vtb=S/t=560/40=14(m/s)
- Chọn đáp án D
9. Giải bài 3.9 trang 13 SBT Vật lý 10
Khi ô tô đang chạy với vận tốc 10 m/s trên đoạn đường thẳng thì người lái xe hãm phanh và ô tô chuyển động chậm dần đều. Cho tới khi dừng hẳn lại thì ô tô đã chạy thêm được 100 m. Gia tốc a của ô tô là bao nhiêu ?
A. a = -0,5 m/s2. C. a = -0,2 m/s2.
B. a = 0,2 m/s2 . D. a = 0,5 m/s2.
Phương pháp giải
Tính gia tốc theo công thức:
\(a = \frac{{{v^2} - v_0^2}}{{2S}}\)
Hướng dẫn giải
- Gia tốc a của ô tô là:
\(\begin{array}{l} {v^2} - v_0^2 = 2aS\\ \Rightarrow a = \frac{{{v^2} - v_0^2}}{{2S}} = \frac{{{0^2} - {{10}^2}}}{{2.100}} = - 0,5(m/{s^2}) \end{array}\)
- Chọn đáp án A
10. Giải bài 3.10 trang 13 SBT Vật lý 10
Hai ô tô chuyển động trên cùng một đường thẳng. Ô tô A chạy nhanh dần và ô tô B chạy chậm dần. So sánh hướng gia tốc của hai ô tô trong mỗi trường hợp sau :
a) Hai ô tô chạy cùng chiều.
b) Hai ô tô chạy ngược chiều.
Phương pháp giải
Vận dụng lí thuyết về chuyển động thẳng biến đổi đều để trả lời câu hỏi này
Hướng dẫn giải
Chọn trục tọa độ trùng với quỹ đạo của hai xe và chiều dương hướng theo chiều chuyển động của xe A.
a) Hai ô tô chạy cùng chiều (Hình 1): Ô tô A chạy theo chiều dương (+) và chuyển động nhanh dần đều nên gia tốc a1 của nó cùng chiều với vận tốc v1. Còn ô tô B cũng chạy theo chiều dương (+) và chuyển động chậm dần đều nên gia tốc a2 của nó ngược chiều với vận tốc v2.
Trong trường hợp này, gia tốc a1 và a2 của hai ô tô ngược hướng (cùng phương, ngược chiều)
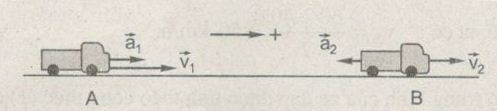
b) Hai ô tô chạy ngược chiều (Hình 2): Ô tô A chạy theo chiều dương (+) và chuyển động nhanh dần nên gia tốc a1 của nó cùng chiều với vận tốc v1. Còn ô tô B chạy ngược chiều dương (+) và chuyển động chậm dần nên gia tốc a2 của nó ngược chiều với vận tốc v2.
Trong trường hợp này, gia tốc a1 và a2 cùng hướng (cùng phương, cùng chiều)
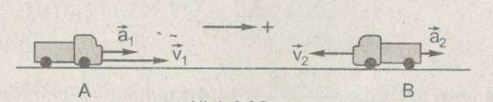
11. Giải bài 3.11 trang 13 SBT Vật lý 10
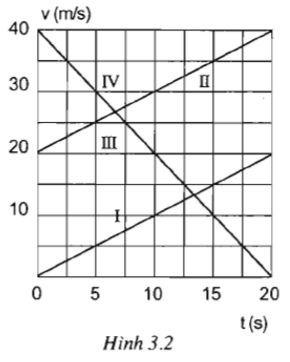
Căn cứ vào đồ thị vận tốc của 4 vật I, II, III, IV trên hình 3.2, hãy lập công thức tính vận tốc và công thức tính quãng đường đi được của mỗi vật chuyển động.
Phương pháp giải
- Dựa vào hình vẽ xác định vo, a và t của từng vật
- Thay các giá trị vào công thức tính vận tốc vận: v=vo+at và quãng đường:
\(s = {v_0}t + \frac{{a{t^2}}}{2} \)
Hướng dẫn giải
- Căn cứ vào đồ thị vận tốc của 4 vật I, II, III, IV vẽ trên hình 3.2 ta có thể xác định được vận tốc đầu v0 và vận tốc tức thời v của mỗi vật chuyển động, do đó tính được gia tốc theo công thức
- Sau đó thay các giá trị tìm được vào công thức tính vận tốc v và công thức tính quãng đường đi được của mỗi vật chuyển động:
- Vật I:
\({v_0} = {\rm{ }}0;{\rm{ }}v = 20{\rm{ }}m/s;{\rm{ }}t = 20{\rm{ }}s;\,v = t;\;s = \frac{{{t^2}}}{2}\)
- Vật II:
\(\begin{array}{l} {v_0} = {\rm{ }}20{\rm{ }}m/s;{\rm{ }}v = 40{\rm{ }}m/s;{\rm{ }}t = 20s;\\ a = \frac{{20}}{{20}} = 1m/{s^2};v = 20{\rm{ }} + {\rm{ }}\;t;s = 20t + \frac{{{t^2}}}{2} \end{array}\)
- Vật III:
\(v = {v_0}\; = 20{\rm{ }}m/s;{\rm{ }}t = 20{\rm{ }}s;{\rm{ }}a = 0;{\rm{ }}s = 20t\)
- Vật IV:
\(\begin{array}{l} {v_0} = 40{\rm{ }}m/s;{\rm{ }}v = 0{\rm{ }}m/s;{\rm{ }}t = 20{\rm{ }}s;\\ a = - \frac{{40}}{{20}} = - 2m/{s^2};v = 40{\rm{ }}-{\rm{ }}2t;s = 40t - {t^2} \end{array}\)
12. Giải bài 3.12 trang 13 SBT Vật lý 10
Khi ô tô đang chạy với vận tốc 12 m/s trên một đoạn đường thẳng thì người lái xe tăng ga cho ô tô chạy nhanh dần đều.
Sau 15 s, ô tô đạt vận tốc 15 m/s.
a) Tính gia tốc của ô tô.
b) Tính vận tốc của ô tô sau 30 s kể từ khi tăng ga.
c) Tính quãng đường ô tô đi được sau 30 s kể từ khi tăng ga.
Phương pháp giải
a) Tính gia tốc vật theo công thức:
\(a = \frac{{v - {v_0}}}{t}\)
b) Tính vận tốc theo công thức:
\(v = {v_0} + at\)
c) Áp dụng công thức:
\(s = {v_0}t + \frac{{a{t^2}}}{2} \) để tính quãng đường vật đi
Hướng dẫn giải
a. Chọn trục tọa độ trùng với quỹ đạo chuyển động thẳng của ô tô, chiều dương của trục hướng theo chiều chuyển động. Chọn mốc thời gian là lúc ô tô bắt đầu tăng ga.
Gia tốc của ô tô bằng:
\(a = \frac{{v - {v_0}}}{t} = \frac{{15 - 12}}{{15}} = 0,2(m/{s^2})\)
b. Vận tốc của ô tô sau 30 s kể từ khi tăng ga:
\(v = {v_0} + at = 12 + 0,2.30 = 18(m/s)\)
c. Quãng đường ô tô đi được sau 30 s kể từ khi tăng ga:
\(s = {v_0}t + \frac{{a{t^2}}}{2} = 12.30 + \frac{{0,{{2.30}^2}}}{2} = 450(m)\)
13. Giải bài 3.13 trang 13 SBT Vật lý 10
Khi đang chạy với vận tốc 36 km/h thì ô tô bắt đầu chạy xuống dốc. Nhưng do bị mất phanh nên ô tô chuyển động thẳng nhanh dần đều với gia tốc 0,2 m/s2 xuống hết đoạn dốc có độ dài 960 m.
a) Tính khoảng thời gian ô tô chạy xuống hết đoạn dốc.
b) Vận tốc ô tô ở cuối đoạn dốc là bao nhiêu ?
Phương pháp giải
a) Tính thời gian theo công thức:
\(s = {v_0}t + \frac{{a{t^2}}}{2}\) (thay số và giải phương trình tìm t , lấy t>0)
b) Áp dụng công thức:
\(v = {v_0} + at\) để tính vận tốc
Hướng dẫn giải
a. Ô tô đang chuyển động với vận tốc v0 = 36 km/h = 10 m/s thì xuống dốc và chuyển động thẳng nhanh dần đều với gia tốc a = 0,2 m/s2.
- Do đó quãng đường ô tô đi được trong khoảng thời gian t là được tính theo công thức \(s = {v_0}t + \frac{{a{t^2}}}{2}\) , thay số vào ta được
\(\begin{array}{l} 960 = 10t + \frac{{0,2{t^2}}}{2}\\ \Rightarrow {t^2} + 100t - 9600 = 0 \end{array}\)
- Do đó giải được t = 60 s.
b. Vận tốc của ô tô ở cuối đoạn dốc là:
\(\begin{array}{l} v = {v_0} + at\\ = 10 + 0,2.60 = 22(m/s) = 79,2(km/h) \end{array}\)
14. Giải bài 3.14 trang 13 SBT Vật lý 10
Một đoàn tàu bắt đầu rời ga và chuyển động thẳng nhanh dần đều. Sau khi chạy được 1,5 km thì đoàn tàu đạt vận tốc 36 km/h. Tính vận tốc của đoàn tàu sau khi chạy được 3 km kể từ khi đoàn tàu bắt đầu rời ga.
Phương pháp giải
Từ công thức độc lập:
\({v^2} - v_0^2 = 2as\) tìm được công thức tính vận tốc là:
\(\begin{array}{l} {v_2} = {v_1}\sqrt {\frac{{{s_2}}}{{{s_1}}}} \end{array}\)
Hướng dẫn giải
- Công thức độc lập với thời gian trong chuyển động thẳng nhanh dần đều là: \({v^2} - v_0^2 = 2as\)
- Gọi v1 là vận tốc của đoàn tàu sau khi đi được đoạn đường s1 = 1,5 km và v2 là vận tốc của đoạn tàu sau khi chạy được đoạn đường s2 = 3 km kể từ khi đoàn tàu bắt đầu rời ga.
- Vì gia tốc a không đổi và vận tốc ban đầu v0 = 0, nên ta có:
\(v_1^2 = 2a{s_1};v_2^2 = 2a{s_2}\)
Do đó:
\(\begin{array}{l} \frac{{v_2^2}}{{v_1^2}} = \frac{{{s_2}}}{{{s_1}}}\\ = > {v_2} = {v_1}\sqrt {\frac{{{s_2}}}{{{s_1}}}} = 36\sqrt {\frac{3}{{1,5}}} = 50,91 \approx 51(km/h) \end{array}\)
15. Giải bài 3.15 trang 14 SBT Vật lý 10
Một viên bi chuyển động thẳng nhanh dần đều không vận tốc đầu trên máng nghiêng và trong giây thứ năm nó đi được quãng đường bằng 36 cm.
a) Tính gia tốc của viên bi chuyển động trên máng nghiêng.
b) Tính quãng đường viên bi đi được sau 5 giây kể từ khi nó bắt đầu chuyển động.
Phương pháp giải
a) Tính gia tốc viên bi theo cách sau:
- Tính quãng đường từng đoạn theo công thức:
\(s = \frac{{a{t^2}}}{2}\)
- Tính quãng đường đi được trong giây thứ 5:
\({\rm{\Delta }}s = {s_5} - {s_4}\)
- Gia tốc được tính theo công thức:
\(a = \frac{{{\rm{\Delta }}s}}{{4,5}}\)
b) Thay t=5 vào công thức quãng đường để tính quãng đường viên bi đi được sau 5s
Hướng dẫn giải
a) Trong chuyển động thẳng nhanh dần đều không vận tốc đầu, quãng đường viên bi đi được sau những khoảng thời gian t liên hệ với gia tốc a theo công thức:
\(s = \frac{{a{t^2}}}{2}\)
- Quãng đường viên bi đi được sau khoảng thời gian t = 4s là:
Và quãng đường viên bi đi được sau khoảng thời gian t = 5s là:
\({s_5} = \frac{{a{{.5}^2}}}{2} = 12,5a\)
- Quãng đường viên bi đi được trong giây thứ 5 là:
\({\rm{\Delta }}s = {s_5} - {s_4} = 4,5a\)
Mà theo đề bài Δs = 36 cm
=> Gia tốc của viên bi là :
\(a = \frac{{{\rm{\Delta }}s}}{{4,5}} = \frac{{36}}{{4,5}} = 8(cm/{s^2})\)
b. Theo kết quả trên, ta tìm được quãng đường viên bi đi được sau khoảng thời gian t = 5s là:
s5 = 12,5.8 = 100 cm.
16. Giải bài 3.16 trang 14 SBT Vật lý 10
Một vật chuyển động thẳng nhanh dần đều có vận tốc đầu là 18 km/h. Trong giây thứ năm, vật đi được quãng đường là 5,9 m.
a) Tính gia tốc của vật.
b) Tính quãng đường vật đi được sau khoảng thời gian là 10 s kể từ khi vật bắt đầu chuyển động.
Phương pháp giải
a) Tính gia tốc viên bi theo cách sau:
- Tính quãng đường từng đoạn theo công thức:
\(s = \frac{{a{t^2}}}{2}\)
- Tính quãng đường đi được trong giây thứ 5:
\({\rm{\Delta }}s = {s_5} - {s_4}\)
- Gia tốc được tính theo công thức:
\(a = \frac{{{\rm{\Delta }}s}}{{4,5}}\)
b) Thay t=10 vào công thức quãng đường để tính quãng đường viên bi đi được sau 10s
Hướng dẫn giải
- Trong chuyển động thẳng nhanh dần đều với vận tốc đầu v0, quãng đường vật đi được sau khoảng thời gian t liên hệ với gia tốc a theo công thức:
\(s = {v_0}t + \frac{{a{t^2}}}{2}\)
- Như vậy quãng đường vật đi được sau khoảng thời gian t = 4 s là:
\({s_4} = {v_0}.4 + \frac{{a{{.4}^2}}}{2} = 4{v_0} + 8a\)
- Và quãng đường vật đi được sau khoảng thời gian t = 5 s là:
\({s_5} = {v_0}.5 + \frac{{a{{.5}^2}}}{2} = 5{v_0} + 12,5a\)
- Do đó quãng đường vật đi được trong giây thứ 5 là:
Δs = s5 – s4 = (5v0 + 12,5a) – (4v0 + 8a) = v0 + 4,5a
Theo đề bài: v0 = 18 km/h = 5 m/s và Δs = 5,9 m nên gia tốc của viên bi bằng
\(a = \frac{{{\rm{\Delta }}s - {v_0}}}{{4,5}} = \frac{{5,9 - 5}}{{4,5}} = 0,2(m/{s^2})\)
b. Theo kết quả trên, ta tìm được quãng đường vật đi được sau khoảng thời gian t = 10 s là:
\({s_{10}} = 5.10 + \frac{{0,{{2.10}^2}}}{2} = 50 + 10 = 60(m)\)
17. Giải bài 3.17 trang 14 SBT Vật lý 10
Khi ô tô đang chạy với vân tốc 15 m/s trên một đoạn đường thẳng thì người lái xe hãm phanh cho ô tô chạy chậm dần đều. Sau khi chạy thêm được 125 m thì vận tốc ô tô chỉ còn bằng 10 m/s.
a) Tính gia tốc của ô tô.
b) Tính khoảng thời gian để ô tô chạy trên quãng đường đó.
Phương pháp giải
a) Tính gia tốc theo công thức:
\(a = \frac{{{v^2} - v_0^2}}{{2s}} \)
b) Tính khoảng thời gian theo công thức:
\(s = {v_0}t + \frac{{a{t^2}}}{2}\) (thay số và giải phương trình tìm t , lấy t>0)
Hướng dẫn giải
a. Chọn trục tọa độ trùng với quỹ đạo chuyển động thẳng của ô tô, chiều dương của trục hướng theo chiều chuyển động. Chọn mốc thời gian là lúc ô tô bắt đầu hãm phanh.
- Theo công thức liên hệ giữa quãng đường đi được với vận tốc và gia tốc trong chuyển động thẳng chậm dần đều:
\({v^2} - v_0^2 = 2as\)
- Ta suy ra công thức tính gia tốc của ô tô:
\(a = \frac{{{v^2} - v_0^2}}{{2s}} = \frac{{{{10}^2} - {{15}^5}}}{{2.125}} = - 0,5(m/{s^2})\)
Dấu – của gia tốc a chứng tỏ ô tô chuyển động thẳng chậm dần đều có chiều dương đã chọn trên trục tọa độ, tức là ngược chiều với vận tốc ban đầu v0.
b. Quãng đường ô tô đi được trong chuyển động thẳng chậm dần đều được tính theo công thức:
\(s = {v_0}t + \frac{{a{t^2}}}{2}\)
- Thay số vào ta được phương trình bậc 2 ẩn t:
- Giải ra ta được hai nghiệm t1 = 50 s và t2 = 10 s.
- Chú ý: Ta loại nghiệm t1 vì thời gian kể từ lúc bắt đầu hãm phanh đến khi dừng lại hẳn (v = 0) là :
\(t = \frac{{v - {v_0}}}{a} = \frac{{0 - 15}}{{ - 0,5}} = 30(s)\,\, < {t_1}\)
Do đó khoảng thời gian để ô tô chạy thêm được 125 m kể từ khi bắt đầu hãm phanh là t2 = 10 s.
18. Giải bài 3.18 trang 14 SBT Vật lý 10
Hai xe máy cùng xuất phát tại hai địa điểm A và B cách nhau 400 m và cùng chạy theo hướng AB trên đoạn đường thẳng đi qua A và B. Xe máy xuất phát từ A chuyển động nhanh dần đều với gia tốc 2,5.10-2 m/s2. Xe máy.xuất phát từ B chuyển động nhanh dần đều với gia tốc 2,0.10-2 m/s2. Chọn A làm mốc, chọn thời điểm xuất phát của hai xe máy làm mốc thời gian và chọn chiều từ A đến B làm chiều dương.
a) Viết phương trình chuyển động của mỗi xe máy.
b) Xác định vị trí và thời điểm hai xe máy đuổi kịp nhau kể từ lúc xuất phát.
c) Tính vận tốc của mỗi xe máy tại vị trí đuổi kịp nhau.
Phương pháp giải
a)- Viết phương trình chuyển động của xe 1 theo dạng:
\({x_1} = \frac{{{a_1}{t^2}}}{2} \)
- Viết phương trình chuyển động của xe 1 theo dạng:
\({x_2} = {x_0} + \frac{{{a_2}{t^2}}}{2} \)
b) Khi hai xe đuổi kịp nhau: x1=x2
⇒ giải phương trình tìm thời gian t
c) Áp dụng công thức: v=at để tính vận tốc mỗi xe
Hướng dẫn giải
a. Phương trình chuyển động của xe máy xuất phát từ A chuyển động nhanh dần đều không vận tốc đầu với gia tốc a1 = 2,5.10-2 m/s2 :
\({x_1} = \frac{{{a_1}{t^2}}}{2} = \frac{{2,{{5.10}^{ - 2}}{t^2}}}{2} = 1,{25.10^{ - 2}}{t^2}\)
Phương trình chuyển động của xe máy xuất phát từ B cách A một đoạn x0 = 400 m chuyển động nhanh dần đều không vận tốc đầu với gia tốc a2 = 2,0.10-2 m/s2 :
\({x_2} = {x_0} + \frac{{{a_2}{t^2}}}{2} = 400 + \frac{{2,{{0.10}^{ - 2}}{t^2}}}{2} = 400 + 1,{0.10^{ - 2}}{t^2}\)
b. Khi hai xe máy gặp nhau thì x1 = x2, nghĩa là:
\(1,{25.10^{ - 2}}{t^2} = 400 + 1,{0.10^{ - 2}}{t^2}\) hay t = 400 s
Như vậy sau thời gian t = 400 s = 6 phút 40 giây kể từ lúc xuất phát thì hai xe đuổi kịp nhau.
Thay vào ta tìm được vị trí hai xe đuổi kịp nhau cách A đoạn:
x1 = 1,25.10-2.4002 = 2000 m = 2 km
c. Tại vị trí gặp nhau của hai xe thì
- Xe xuất phát từ A có vận tốc bằng :
\({v_1} = {a_1}t = 2,{5.10^{ - 2}}.400 = 10(m/s) = 36(km/h)\)
- Xe xuất phát từ B có vận tốc bằng:
\({v_2} = {a_2}t = 2,{0.10^{ - 2}}.400 = 8(m/s) = 28,8(km/h)\)
Tham khảo thêm
- doc Giải bài tập SBT Vật Lí 10 Bài 1: Chuyển động cơ
- doc Giải bài tập SBT Vật Lí 10 Bài 2: Chuyển động thẳng đều
- doc Giải bài tập SBT Vật Lí 10 Bài 4: Sự rơi tự do
- doc Giải bài tập SBT Vật Lí 10 Bài 5: Chuyển động tròn đều
- doc Giải bài tập SBT Vật Lí 10 Bài 6: Tính tương đối của chuyển động. Công thức cộng vận tốc
- doc Giải bài tập SBT Vật Lí 10 Bài tập cuối chương I: Động học chất điểm



