Giải bài tập SBT Vật Lí 10 Bài 29: Quá trình đẳng nhiệt. Định luật Bôi-lơ-Ma-ri-ốt

Tập hợp ba thông số nào sau đây xác định trạng thái của một lượng khí xác định ?

A. Áp suất, thể tích, khối lượng.

B. Áp suất, nhiệt độ, thể tích.

C. Thể tích, trọng lượng, áp suất.

D. Áp suất, nhiệt độ, khối lượng.

Phương pháp giải

3 thông số trạng thái của chất khí: áp suất, nhiệt độ, thể tích

Hướng dẫn giải

- Tập hợp ba thông số áp suất, nhiệt độ, thể tích là trạng thái của một lượng khí xác định

- Chọn B

Quá trình nào sau đây là đẳng quá trình ?

A. Đun nóng khí trong một bình đậy kín.

B. Không khí trong quả bóng bay bị phơi nắng, nóng lên, nở ra làm căng bóng.

C. Đun nóng khí trong một xilanh, khí nở ra đẩy pit-tông chuyển động.

D. Cả ba quá trình trên đều không phải là đẳng quá trình.

Phương pháp giải

Đẳng quá trình là quá trình biến đổi trạng thái của chất khí mà có một trong 3 thông số trạng thái không đổi

Hướng dẫn giải

A - đúng vì trong quá trình thay đổi trạng thái, thể tích khí là không đổi do bình kín, gọi là quá trình đẳng tích 

⇒ Chọn đáp án A

Đẩy pit-tông của một xilanh đủ chậm để nén lượng khí chứa trong xilanh sao cho thể tích của lượng khí này giảm đi 2 lần ở nhiệt độ không đổi. Khi đó áp suất của khí trong xi lanh

A. giảm đi 2 lần.                                B. tăng lên 2 lần.

C. tăng thêm 4 lần.                           D. không thay đổi.

Phương pháp giải

Áp dụng định luật Bôi lơ ma ri ốt:

\({p_1}{V_1} = {p_2}{V_2}\) để tìm p₂

Hướng dẫn giải

- Ta có: 

\(\begin{array}{l} {V_1} = 2{V_2}\\ {p_1}{V_1} = {p_2}{V_2}\\ \Rightarrow {p_2} = \frac{{{p_1}{V_1}}}{{{V_2}}} = \frac{{{p_1}.2{V_2}}}{V} = 2{p_1} \end{array}\)

- Chọn đáp án B

Hệ thức nào sau đây là của định luật Bôi-lơ - Ma-ri-ốt ?

A. p₁V₂ = p₂V₁.                        B. p/V = hằng số.

C. pV = hằng số.                      D. V/p = hằng số.

Phương pháp giải

Công thức định luật Bôi lơ ma ri ốt: 

\({p_1}{V_1} = {p_2}{V_2}\) hay pV=const

Hướng dẫn giải

- Hệ thức pV = hằng số là của định luật Bôi-lơ - Ma-ri-ốt

- Chọn C

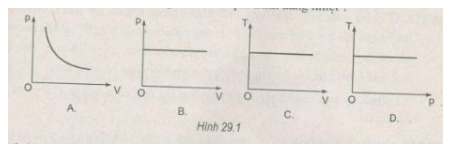
Đường nào sau đây không biểu diễn quá trình đẳng nhiệt?

Phương pháp giải

Quá trình đẳng nhiệt là quá trình biến đổi trạng thái trong đó nhiệt độ được giữ không đổi

Hướng dẫn giải

Hình A, C, D - đều có nhiệt độ không đổi

Hình B - có áp suất p không đổi

⇒ Chọn đáp án B

Một lượng khí có thể tích 1 m³ và áp suất 1 atm. Người ta nén đẳng nhiệt khí tới áp suất 3,5 atm. Thể tích của khí nén là

A. 28,6 m³

B. 3,5 m³

C. 0,286 m³

D. 0,35 m³

Phương pháp giải

Áp dụng định luật Bôi lơ ma ri ốt: 

\({p_1}{V_1} = {p_2}{V_2}\) để tính V₂

Hướng dẫn giải

- Ta có:

\(\begin{array}{l} {p_1}{V_1} = {p_2}{V_2}\\ \Rightarrow {V_2} = \frac{{{p_1}{V_1}}}{{{p_2}}} = \frac{{1.1}}{{3,5}} = 0,286{m^3} \end{array}\)

- Chọn đáp án C

Một bình đựng khí có dung tích 6.10⁻³m³ đựng khí ở áp suất 2,75.10⁶Pa. Người ta dùng khí trong bình để thổi các quả bóng bay sao cho bóng có thể tích 3.10⁻³m³ và khí trong bóng có áp suất 1,1.10⁵Pa. Nếu coi nhiệt độ của khí không đổi thì số lượng bóng thổi được là

A. 50 quả bóng

B. 48 quả bóng

C. 52 quả bóng

D. 49 quả bóng

Phương pháp giải

Áp dụng định luật Bôi lơ ma ri ốt:

\({p_2}(n{V_2} + {V_1}) = {p_2}(n + 2)V\) để tính số lượng bóng thổi được

Hướng dẫn giải

- Khí trong bình chỉ thổi được bóng cho tới khi áp suất của khí trong bình bằng áp suất của khí trong bóng: 

\({p_1}{V_1} = {p_2}V_2^\prime = {p_2}(n{V_2} + {V_1}) = {p_2}(n + 2){V_2}\)

Thay số: 

\(\begin{array}{l} {2,75.10^6}{.6.10^{ - 3}} = {1,1.10^5}(n + 2){.3.10^{ - 3}}\\ \Rightarrow n = 48 \end{array}\)

- Chọn đáp án B

Người ta điều chế khí hiđrô và chứa vào một bình lớn dưới áp suất 1 atm, ở nhiệt độ 20°C. Tính thể tích khí phải lấy từ bình lớn ra để nạp vào một bình nhỏ thể tích 20 lít dưới áp suất 25 atm. Coi nhiệt độ không đổi.

Phương pháp giải

Áp dụng định luật Bôi lơ ma ri ốt:

\({p_1}{V_1} = {p_2}{V_2}\) để tính thể tích

Hướng dẫn giải

Ta có:

\(\begin{array}{l} {p_1}{V_1} = {p_2}{V_2}\\ \Rightarrow {V_1} = \frac{{{p_2}{V_2}}}{{{p_1}}} = \frac{{25.20}}{1} = 500 \end{array}\)

Vậy thể tích khí phải lấy từ bình lớn là 500 lít

Tính khối lượng khí ôxi đựng trong một bình thể tích 10 lít dưới áp suất 150 atm ở nhiệt độ 0°C. Biết ở điều kiện chuẩn khối lượng riêng của ôxi là 1,43 kg/m³.

Phương pháp giải

- Áp dụng công thức quá trình đẳng tích:

ρ₀V₀=ρV để tính ρ

- Tính khối lượng theo công thức: m=ρ.V 

Hướng dẫn giải

Biết ρ₀=m/V₀ và ρ=m/V suy ra  ρ₀V₀=ρV

Vì nhiệt độ của khí bằng nhiệt độ ở điều kiện chuẩn nên

\(\rho = \frac{{{\rho _0}p}}{{{p_0}}} = \frac{{1,43.150}}{1} = 214,5(kg/{m^3})\)

Và m = 214,5.10^-2 = 2,145 kg.

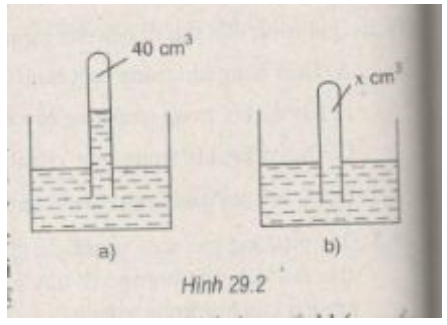
Một ống thuỷ tinh được cắm lộn ngược vào một chậu chứa thuỷ ngân, bên trong ống chứa 40 cm³ không khí và một cột thuỷ ngân cao 8 cm so với mực thuỷ ngân trong chậu (H.29.2a). Người ta ấn sâu ống thủy tinh vào thủy ngân cho tới khi mực thủy ngân ở bên trong và bên ngoài ống bằng nhau (H.29.2b). Tính thể tích của không khí còn lại bên trong ống thủy tinh. Biết áp suất khí quyển là 75 cmHg.

Phương pháp giải

Áp dụng công thức:

\({V_2} = \frac{{{p_1}{V_1}}}{{{p_2}}}\) để tính thể tích không khí còn lại bên trong ống thủy tinh

Hướng dẫn giải

Vì nhiệt độ không đổi nên:

\({p_1}{V_1} = {p_2}{V_2}\)

⇒ \({V_2} = \frac{{{p_1}{V_1}}}{{{p_2}}} \approx 35,7(c{m^3})\)

Ớ chính giữa một ống thuỷ tinh nằm ngang, tiết diện nhỏ, chiều dài L = 100 cm, hai đầu bịt kín có một cột thuỷ ngân dài h = 20 cm. Trong ống có không khí. Khi đặt ống thẳng đứng, cột thuỷ ngân dịch chuyển xuống dưới một đoạn l = 10 cm. Tìm áp suất của không khí trong ống ra cmHg và Pa khi ống nằm ngang.
Coi nhiệt độ của không khí trong ống không đổi và khối lượng riêng của thuỷ ngân là ρ=1,36.104kg/m³

Phương pháp giải

- Xác định thông số trạng thái của từng khối khí ( ở hai bên cột thủy ngân, ở trên cột thủy ngân, ở dưới cột thủy ngân)

- Áp dụng định luật Bôi lơ Mariot cho từng khối khí, ta có:

+ \({p_2} = \frac{{h(L - h - 2\ell )}}{{4\ell }}\)

+ \({p_1} = \frac{{h({{(L - h)}^2} - 4{\ell ^2})}}{{4\ell (L - h)}}\)

thay số để tìm áp suất của không khí trong ống

Hướng dẫn giải

- Trạng thái 1 của mỗi lượng khí ở hai bên cột thủy ngân (ống nằm ngang)

\({p_1};{V_1} = \frac{{L - h}}{2}S;{T_1}\)

- Trạng thái 2 (ống đứng thẳng)

- Đối với lượng khí ở trên cột thủy ngân: 

\({p_2};{V_2} = (\frac{{L - h}}{2} + \ell )S;{T_2} = {T_1}\)

- Đối với lượng khí ở dưới cột thủy ngân: 

\(p_2^\prime ;V_2^\prime = (\frac{{L - h}}{2} + \ell )S;T_2^\prime = {T_1}\)

Áp suất khí ở phần dưới bằng áp suất khí ở phần trên cộng với áp suất do cột thủy ngân gây ra. Do đó đối với khí ở phần dưới, ta có: 

\(p_2^\prime = {p_2} + h;V_2^\prime = (\frac{{L - h}}{2} - \ell )S;T_2^\prime = {T_1}\)

Áp dụng định luật Bôi lơ ma ri ốt cho từng lượng khí. Ta có:

- Đối với khí ở trên:

\(\begin{array}{l} {p_1}\frac{{L - h}}{2}S = {p_2}(\frac{{L - h + 2\ell }}{2})S\\ \Rightarrow {p_1}(L - h) = {p_2}(L - h + 2\ell ) \end{array}\)

- Đối với khí ở dưới:

\(\begin{array}{l} {p_1}\frac{{L - h}}{2}S = ({p_2} + h)(\frac{{L - h - 2\ell }}{2})S\\ \Rightarrow {p_1}(L - h) = ({p_2} + h)(L - h - 2\ell ) \end{array}\)

Từ hai phương trình (1) và (2) rút ra:

\({p_2} = \frac{{h(L - h - 2\ell )}}{{4\ell }}\)

Thay giá trị của p₂ vào (1) ta được:

\(\begin{array}{l} {p_1} = \frac{{h({{(L - h)}^2} - 4{\ell ^2})}}{{4\ell (L - h)}}\\ {p_1} = \frac{{20({{(100 - 20)}^2} - {{4.10}^2})}}{{4.10.(100 - 20)}} = 37,5cmHg\\ {p_1} = \rho gh = {1,36.10^4}.9,8.0,375 = {5.10^4}Pa \end{array}\)

Ở chính giữa một ống thuỷ tinh nằm ngang, kín cả hai đầu có một cột thuỷ ngân dài h = 19,6 mm. Nếu đặt ống nghiêng một góc 30° so với phương nằm ngang thì cột thuỷ ngân dịch chuyển một đoạn Δl₁ = 20 mm. Nếu đặt ống thẳng đứng thì cột thuỷ ngân dịch chuyển một đoạn Δl₂ = 30 mm.

Xác định áp suất của không khí trong ống khi ống nằm ngang. Coi nhiệt độ không đổi.

Phương pháp giải

- Xác định thông số trạng thái của: không khí trong ống nằm ngang; không khí khi ống nằm nghiêng; không khí khi ống thẳng đứng

- Áp dụng định luật Bôi lơ để tìm các giá trị đoạn dịch chuyển khi ống nằm nghiêng và khi ống thẳng đứng

- Khi cột thủy ngân cân bằng, ta có công thức:

p₂ = p’₂ + ρghsinα và p₃ = p’₃ + ρgh

- Từ các giá trị trên, tìm p₂ theo công thức:

\(\begin{array}{l} {p_1} = \frac{{\rho gh}}{2}\left( {\sqrt {\frac{{{\rm{\Delta }}{l_1}\left( {{\rm{\Delta }}{l_2} - {\rm{\Delta }}{l_1}\sin \alpha } \right)}}{{{\rm{\Delta }}{l_2}\left( {{\rm{\Delta }}{l_1} - {\rm{\Delta }}{l_2}\sin \alpha } \right)}}} - \sqrt {\frac{{{\rm{\Delta }}{l_2}\left( {{\rm{\Delta }}{l_1} - {\rm{\Delta }}{l_2}\sin \alpha } \right)}}{{{\rm{\Delta }}{l_1}\left( {{\rm{\Delta }}{l_2} - {\rm{\Delta }}{l_1}\sin \alpha } \right)}}} } \right)\\ \end{array}\)

Hướng dẫn giải

- Trạng thái 1 của không khí trong ống nằm ngang. Với lượng khí ở bên phải cũng như ở bên trái cột thủy ngân: p₁; V₁.

- Trạng thái 2 của không khí khi ống nằm nghiêng.

+ Với lượng khí ở bên trái: p₂ ; V₂.

+ Với lượng khí ở bên phải: p’₂ ; V’₂.

- Trạng thái 3 của không khí khi ống thẳng đứng.

+ Với lượng khí ở bên trái: p₃ ;  V₃.

+ Với lượng khí ở bên phải: p’₃ ; V’₃.

- Theo định luật Bôi-lơ – Ma-ri-ốt. Ta có:

+ Khi ống nằm nghiêng thì: l₂ = l₁ – Δl₁ và l’₂ = l₁ + Δl₁

+ Khi ống thẳng đứng thì: l₃ = l₁ – Δl₂ và l’₃ = l₁ + Δl₂

- Ngoài ra, khi cột thủy ngân đã cân bằng thì:

p₂ = p’₂ + ρghsinα và p₃ = p’₃ + ρgh.

Thay các giá trị của l₂, l₃, l’₂, l’₃, p₂, p₃ vào các phương trình của định luật Bôi-lơ – Ma-ri-ốt ở trên, ta được:

\(\begin{array}{l} {p_1} = \frac{{\rho gh}}{2}\left( {\sqrt {\frac{{{\rm{\Delta }}{l_1}\left( {{\rm{\Delta }}{l_2} - {\rm{\Delta }}{l_1}\sin \alpha } \right)}}{{{\rm{\Delta }}{l_2}\left( {{\rm{\Delta }}{l_1} - {\rm{\Delta }}{l_2}\sin \alpha } \right)}}} - \sqrt {\frac{{{\rm{\Delta }}{l_2}\left( {{\rm{\Delta }}{l_1} - {\rm{\Delta }}{l_2}\sin \alpha } \right)}}{{{\rm{\Delta }}{l_1}\left( {{\rm{\Delta }}{l_2} - {\rm{\Delta }}{l_1}\sin \alpha } \right)}}} } \right)\\ = 6mmHg \end{array}\)

Người ta dùng bơm có pit-tông diện tích 8 cm² và khoảng chạy 25 cm bơm một bánh xe đạp sao cho áp lực của bánh xe đạp lên mặt đường là 350 N  thì diện tích tiếp xúc là 50 cm². Ban đầu bánh xe đạp chứa không khí ở áp suất khí quyển p₀ = 10⁵ Pa và có thể tích là V₀ = 1 500 cm³. Giả thiết khi áp suất không khí trong bánh xe đạp vượt quá 1,5p₀ thì thể tích của bánh xe đạp là 2 000 cm³.

a) Hỏi phải đẩy bơm bao nhiêu lần ?

b) Nếu do bơm hở nên mỗi lần đẩy bơm chỉ đưa được 100 cm³ không khí vào bánh xe thì phải đẩy bao nhiêu lần ?

Phương pháp giải

a) Áp dụng định luật Bôi-lơ – Ma-ri-ốt để tìm n với:

- p₁ = p₀ ; V₁ = (1500 + 200n)

- p₂ = 1,7.10⁵ Pa ; V₂ = 2000 cm³

b) Tìm số lần đẩy bơm theo công thức:  n’ = 2n

Hướng dẫn giải

Áp suất trong bánh xe khi bơm xong: p = p₀ + p’

Với p’ = 350/0,005 = 0,7.10⁵ Pa; p = 1,7.10⁵ Pa lớn hơn 1,5p₀ nên thể tích sau khi bơm là 2000 cm³.

a) Mỗi lần bơm có 8.25 = 200 cm³ không khí ở áp suất p₀ được đưa vào bánh xe. Sau n lần bơm có 200n cm³ không khí được đưa vào bánh. Ban đầu có 1500 cm³ không khí ở áp suất p0 trong bánh xe. Như vậy có thể coi:

- Trạng thái 1: p₁ = p₀ ; V₁ = (1500 + 200n)

- Trạng thái 2: p₂ = 1,7.10⁵ Pa ; V₂ = 2000 cm³

- Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần.

b) n’ = 2n = 19 lần.