Giải bài tập SBT Vật Lí 10 Bài 22: Ngẫu lực
Mời các em học sinh cùng tham khảo nội dung giải bài 22 SBT Vật Lý 10 dưới đây. Hy vọng đây sẽ là tài liệu hữu ích giúp các em rèn luyện phương pháp giải bài tập khi có ngẫu lực tác dụng vào vật.
Mục lục nội dung

1. Giải bài 22.1 trang 50 SBT Vật lý 10
Một ngẫu lực \(\vec F,\overrightarrow {F'} \) tác dụng vào một thanh cứng như hình 22.1. Momen của ngẫu lực tác dụng vào thanh đối với trục O là bao nhiêu ?
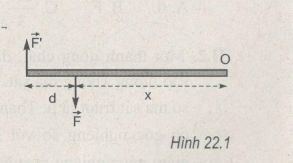
A. (Fx + Fd). B. (Fd - Fx).
C. (Fx - Fd). D. Fd.
Phương pháp giải
Fd là momen của ngẫu lực tác dụng vào thanh đối với trục O
Hướng dẫn giải
- Momen của ngẫu lực tác dụng vào thanh đối với trục O là Fd.
- Chọn đáp án D
2. Giải bài 22.2 trang 50 SBT Vật lý 10
Một cái chắn đường có trọng lượng 600N quay quanh trục nằm ngang O. Trục quay này cũng là trục quay của động cơ điện dùng để nâng chắn đường lên. Trọng tâm G của chắn đường cách O: 50 cm. Để nâng chắn đường lên, momen ngẫu lực của động cơ phải có độ lớn tối thiểu là
A. 300 N.m
B. 150 N.m
C. 1200 N.m
D. 600 N.m
Phương pháp giải
Áp dụng công thức tính momen của ngẫu lực:
M=F.d
Hướng dẫn giải
- Momen của ngẫu lực là:
MF=MP=Pd=600.0,5=300N.m
- Chọn đáp án A
3. Giải bài 22.3 trang 50 SBT Vật lý 10
Tác dụng của ngẫu lực đối với một vật có thay đổi không nếu ta thay đổi điểm đặt và phương của cặp lực (F, F') nhưng không thay đổi độ lớn của lực và cánh tay đòn của ngẫu lực (H.22.2 a và b)?
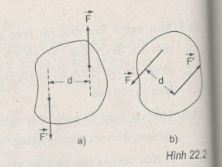
Phương pháp giải
Khi độ lớn của lực và cánh tay đòn không đổi thì ngẫu lực cũng không thay đổi
Hướng dẫn giải
Ngẫu lực trong trường hợp này không đổi
4. Giải bài 22.4 trang 50 SBT Vật lý 10
Một vật rắn phẳng, mỏng có dạng là một tam giác đều ABC, mỗi cạnh là a = 20 cm. Người ta tác dụng vào vật một ngẫu lực nằm trong mặt phẳng của tam giác. Các lực có độ lớn là 8 N và đặt vào hai đỉnh A và B. Tính momen của ngẫu lực trong các trường hợp sau đây :
a) Các lực vuông góc với cạnh AB.
b) Các lực vuông góc với cạnh AC.
c) Các lực song song với cạnh AC.
Phương pháp giải
Áp dụng công thức: M=F.d để tính momen cho từng trường hợp
Hướng dẫn giải
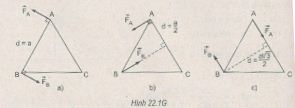
Áp dụng công thức tính momen ngẫu lực M = F.d vào các phần ta được
a. M = F.d = F.a = 8.0,2 = 1,6 N.m
b. M = F.d = F.a/2 = 8.0,1 = 0,8 N.m
c. M = F.d = F. \(a\frac{{\sqrt 3 }}{2}\) = 8. 0,1.\(\frac{{\sqrt 3 }}{2}\) = 1,38 N.m
Tham khảo thêm
- doc Giải bài tập SBT Vật Lí 10 Bài 17: Cân bằng của một vật chịu tác dụng của hai lực và của ba lực không song song
- doc Giải bài tập SBT Vật Lí 10 Bài 18: Cân bằng của một vật có trục quay cố định. Momen lực
- doc Giải bài tập SBT Vật Lí 10 Bài 19: Quy tắc hợp lực song song cùng chiều
- doc Giải bài tập SBT Vật Lí 10 Bài 20: Các dạng cân bằng. Cân bằng của một vật có mặt chân đế
- doc Giải bài tập SBT Vật Lí 10 Bài 21: Chuyển động tịnh tiến của vật rắn. Chuyển động quay của vật rắn quanh một trục cố định
- doc Giải bài tập SBT Vật Lí 10 Bài tập cuối chương III: Cân bằng và chuyển động của vật rắn



