Giải bài tập SBT Toán 12 Bài 3: Phương trình đường thẳng
Môn Toán là môn quan trọng và tương đối khó với các em học sinh lớp 12, với mong muốn giúp các em nắm thật vững kiến thức và làm bài thật hiệu quả eLib đã biên soạn và tổng hợp nội dung giải bài tập SBT trang 130 - 132 bên dưới đây. Với nội dung chi tiết, rõ ràng được trình bày logic, khoa học hứa hẹn sẽ mang lại cho các em thật nhiều kiến thức bổ ích.
Mục lục nội dung
1. Giải bài 3.31 trang 130 SBT Hình học 12
2. Giải bài 3.32 trang 130 SBT Hình học 12
3. Giải bài 3.33 trang 130 SBT Hình học 12
4. Giải bài 3.34 trang 130 SBT Hình học 12
5. Giải bài 3.35 trang 130 SBT Hình học 12
6. Giải bài 3.36 trang 131 SBT Hình học 12
7. Giải bài 3.37 trang 131 SBT Hình học 12
8. Giải bài 3.38 trang 131 SBT Hình học 12
9. Giải bài 3.39 trang 131 SBT Hình học 12
10. Giải bài 3.40 trang 131 SBT Hình học 12
11. Giải bài 3.41 trang 132 SBT Hình học 12
12. Giải bài 3.42 trang 132 SBT Hình học 12
13. Giải bài 3.43 trang 132 SBT Hình học 12

1. Giải bài 3.31 trang 130 SBT Hình học 12
Viết phương trình tham số, phương trình chính tắc của đường thẳng Δ trong các trường hợp sau:
a) Δ đi qua điểm A(1; 2; 3) và có vecto chỉ phương \(\overrightarrow a = (3;3;1)\)
b) Δ đi qua điểm B(1; 0; -1) và vuông góc với mặt phẳng (α) : 2x – y + z + 9 = 0
c) Δ đi qua hai điểm C(1; -1; 1) và D(2; 1; 4)
Phương pháp giải
a) Đường thẳng đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có VTCP \(\overrightarrow u = \left( {a;b;c} \right)\) có phương trình tham số là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) và phương trình chính tắc \(\dfrac{{x - {x_0}}}{a} = \dfrac{{y - {y_0}}}{b} = \dfrac{{z - {z_0}}}{c}\)
b) Đường thẳng Δ vuông góc mặt phẳng \(\left( \alpha \right)\) thì \(\overrightarrow {{u_\Delta }} = \overrightarrow {{n_{\left( \alpha \right)}}} \)
c) Đường thẳng Δ đi qua hai điểm C,D thì \(\overrightarrow {{u_\Delta }} = \overrightarrow {CD}\)
Hướng dẫn giải
a) Phương trình tham số của đường thẳng Δ đi qua điểm A(1; 2; 3) và có vecto chỉ phương \(\overrightarrow a = (3;3;1)\) là: \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + 3t}\\{y = 2 + 3t}\\{z = 3 + t}\end{array}} \right.\)
Phương trình chính tắc của Δ là \(\dfrac{{x - 1}}{3} = \dfrac{{y - 2}}{3} = \dfrac{{z - 3}}{1}\)
b) \(\Delta \bot (\alpha ) \Rightarrow \overrightarrow {{u_\Delta }} = \overrightarrow {{n_{\left( \alpha \right)}}} = (2; - 1;1)\)
Phương trình tham số của Δ là \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = - t}\\{z = - 1 + t}\end{array}} \right.\)
Phương trình chính tắc của Δ là \(\dfrac{{x - 1}}{2} = \dfrac{y}{{ - 1}} = \dfrac{{z + 1}}{1}\)
c) Δ đi qua hai điểm C và D nên có vecto chỉ phương \(\overrightarrow {CD} = (1;2;3)\)
Vậy phương trình tham số của Δ là \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = - 1 + 2t}\\{z = 1 + 3t}\end{array}} \right.\)
Phương trình chính tắc của Δ là \(\dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{3}\)
2. Giải bài 3.32 trang 130 SBT Hình học 12
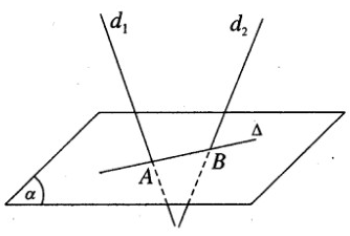
Viết phương trình của đường thẳng Δ nằm trong mặt phẳng (α): x + 2z = 0 và cắt hai đường kính \({d_1}:\left\{ {\begin{array}{*{20}{c}}{x = 1 - t}\\{y = t}\\{z = 4t}\end{array}} \right.\) và \({d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 2 - t'}\\{y = 4 + 2t'}\\{z = 4}\end{array}} \right.\)
Phương pháp giải
- Tham số hóa tọa độ hai giao điểm.
- Thay tọa các điểm vào phương trình mặt phẳng \(\left( \alpha \right)\), từ đó suy ra tọa độ các điểm.
- Viết phương trình đường thẳng đi qua hai điểm và kết luận.
Hướng dẫn giải
Gọi A và B lần lượt là giao điểm của d1 và d2 với (α). Đường thẳng Δ cần tìm chính là đường thẳng AB.
Ta có: A(1 − t; t; 4t) ∈ d1
A ∈ (α) ⇔ t + 4.(2t) = 0 ⇔ t = 0
Suy ra: A(1; 0; 0)
Ta có : B(2 − t′; 4 + 2t′; 4) ∈ d2
B ∈ (α) ⇔ 4 +2t′ + 8 = 0 ⇔ t′ = −6
Suy ra B(8; -8; 4)
Δ đi qua A, B nên có vecto chỉ phương \(\overrightarrow {{u_\Delta }} = \overrightarrow {AB} = (7; - 8;4)\)
Phương trình chính tắc của Δ là:
\(\dfrac{{x - 1}}{7} = \dfrac{y}{{ - 8}} = \dfrac{z}{4}\)
3. Giải bài 3.33 trang 130 SBT Hình học 12
Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau:
a) \(d:\dfrac{{x + 1}}{1} = \dfrac{{y - 1}}{2} = \dfrac{{z + 3}}{3} \,\, và \,\,d':\dfrac{{x - 1}}{3} = \dfrac{{y - 5}}{2} = \dfrac{{z - 4}}{2}\)
b) \(d:\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = 1 + t}\\{z = 2 - t}\end{array}} \right. \,\, và \,\, d':\left\{ {\begin{array}{*{20}{c}}{x = 9 + 2t'}\\{y = 8 + 2t'}\\{z = 10 - 2t'}\end{array}} \right.\)
c) \(d:\left\{ {\begin{array}{*{20}{c}}{x = - t}\\{y = 3t}\\{z = - 1 - 2t}\end{array}} \right. \,\, và \,\, d':\left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = 9}\\{z = 5t'}\end{array}} \right.\)
Phương pháp giải
Sử dụng lý thuyết về vị trí tương đối của hai đường thẳng.
Cho đường thẳng ∆1 qua điểm M1 và có vec tơ chỉ phương \(\overrightarrow{u_{1}}\), đường thẳng ∆2 qua điểm M2 và có vec tơ chỉ phương \(\overrightarrow{u_{2}}\)
* ∆1 và ∆2 chéo nhau ⇔ ∆1 và ∆2 không nằm trong cùng một mặt phẳng ⇔ \(\left [\overrightarrow{u_{1}},\overrightarrow{u_{2}} \right ]\overrightarrow{M_{1}M_{2}}\neq 0\)
* ∆1 và ∆2 song song ⇔ \(\left\{\begin{matrix} \overrightarrow{u_{1}}=k\overrightarrow{u_{2}}\\ M_{1}\in \Delta _{1}\\ M_{2}\notin \Delta _{2} \end{matrix}\right.\)
* ∆1 trùng với ∆2 ⇔ \(\overrightarrow{u_{1}}, \overrightarrow{u_{2}}, \overrightarrow{M_{1}M_{2}}\) là ba vectơ cùng phương.
* ∆1 cắt ∆2 ⇔ \(\overrightarrow{u_{1}},\overrightarrow{u_{2}}\) không cùng phương và \(\left [\overrightarrow{u_{1}},\overrightarrow{u_{2}} \right ]\overrightarrow{M_{1}M_{2}}= 0\)
Hướng dẫn giải
a) Ta có: \(\overrightarrow {{u_d}} = (1;2;3)\) và \(\overrightarrow {{u_{d'}}} = (3;2;2)\)
Suy ra \(\overrightarrow n = \left[ {\overrightarrow {{u_d}} ,\overrightarrow {{u_{d'}}} } \right] = ( - 2;7; - 4)\)
Ta có \({M_0}( - 1;1; - 2) \in d,{M_0}'(1;5;4) \in {\rm{d'}} \Rightarrow \overrightarrow {{M_0}{M_0}'} = (2;4;6)\)
Ta có \(\overrightarrow n .\overrightarrow {{M_0}{M_0}'} = - 4 + 28 - 24 = 0\)
Vậy đường thẳng d và d’ đồng phẳng và khác phương, nên d và d’ cắt nhau.
b) Ta có \(\overrightarrow {{u_d}} = (1;1; - 1)\) và \(\overrightarrow {{u_{d'}}} = (2;2; - 2).{M_0}(0;1;2) \in d\)
Vì \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{u_{d'}}} = 2\overrightarrow {{u_d}} }\\{{M_0} \notin d'}\end{array}} \right.\) (tọa độ M0 không thỏa mãn d’) nên hai đường thẳng d và d’ song song.
c) d có vecto chỉ phương \(\overrightarrow {{u_d}} = ( - 1;3; - 2)\)
d’ có vecto chỉ phương \(\overrightarrow {{u_{d'}}} = (0;0;5)\)
Gọi \(\overrightarrow n = \left[ {\overrightarrow {{u_d}} ,\overrightarrow {{u_{d'}}} } \right] = (15;5;0) \ne \overrightarrow 0\)
Ta có \({M_0}(0;0; - 1) \in d\)
\(M{'_0}(0;9;0) \in d' \Rightarrow \overrightarrow {{M_0}M{'_0}} = (0;9;1),\overrightarrow n .\overrightarrow {{M_0}M{'_0}} = 45 \ne 0\)
Vậy d và d’ là hai đường thẳng chéo nhau.
4. Giải bài 3.34 trang 130 SBT Hình học 12
Tìm a để hai đường thẳng sau đây song song: \(d:\left\{ {\begin{array}{*{20}{c}}{x = 5 + t}\\{y = at}\\{z = 2 - t}\end{array}} \right.\) và \(d':\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t'}\\{y = a + 4t'}\\{z = 2 - 2t'}\end{array}} \right.\)
Phương pháp giải
- Sử dụng điều kiện cần, hai đường thẳng song song thì \(\overrightarrow {{u_d}} //\overrightarrow {{u_{d'}}} \,\, tìm \,\,a\)
- Thay a và kiểm tra lại điều kiện d//d'.
Hướng dẫn giải
Ta có \(\overrightarrow {{u_d}} = (1;a; - 1) \,\, và \,\, \overrightarrow {{u_{d'}}} = (2;4; - 2)\)
\(d//d' \Rightarrow \dfrac{1}{2} = \dfrac{a}{4} = \dfrac{{ - 1}}{{ - 2}} \Rightarrow a = 2\)
Khi đó \(M{'_0}(1;2;2)\) thuộc d’ và M’0 không thuộc d.
Vậy d//d' nếu a = 2.
5. Giải bài 3.35 trang 130 SBT Hình học 12
Xét vị trí tương đối của đường thẳng d với mặt phẳng \((\alpha )\) trong các trường hợp sau
a) \(d:\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = 1 + 2t}\\{z = 1 - t}\end{array}} \right.\) và \((\alpha) : x + 2y + z - 3 = 0\)
b) d: \(\left\{ {\begin{array}{*{20}{c}}{x = 2 - t}\\{y = t}\\{z = 2 + t}\end{array}} \right.\) và \((\alpha) : x + z + 5 = 0\)
c) \(d:\left\{ {\begin{array}{*{20}{c}}{x = 3 - t}\\{y = 2 - t}\\{z = 1 + 2t}\end{array}} \right. \,\, và \, \, (\alpha ) : x +y + z -6 = 0\)
Phương pháp giải
Thay x, y, z trong phương trình đường thẳng vào phương trình mặt phẳng, kiểm tra nghiệm.
- Phương trình có nghiệm duy nhất thì đường thẳng cắt mặt phẳng.
- Phương trình vô nghiệm thì đường thẳng song song mặt phẳng.
- Phương trình vô số nghiệm thì đường thẳng nằm trong mặt phẳng.
Hướng dẫn giải
a) Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình tổng quát của mặt phẳng \((\alpha)\) ta được: \(t + 2\left( {1 + 2t} \right) + \left( {1 - t} \right) - 3 = 0 \Leftrightarrow 4t = 0 \Leftrightarrow t = 0\)
Vậy đường thẳng d cắt mặt phẳng \((\alpha )\) tại M0(0; 1; 1).
b) Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của \((\alpha )\) ta được: \(\left( {2 - t} \right)\; + \left( {2 + t} \right) + 5 = 0 \Leftrightarrow 0t = - 9\)
Phương trình vô nghiệm, vậy đường thẳng d song song với \((\alpha )\)
c) Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của \((\alpha )\) ta được: \(\left( {3 - t} \right) + \left( {2 - t} \right) + \left( {1 + 2t} \right) - 6 = 0 \Leftrightarrow 0t\; = 0\)
Phương trình luôn thỏa mãn với mọi t.
Vậy d nằm trong \((\alpha )\)
6. Giải bài 3.36 trang 131 SBT Hình học 12
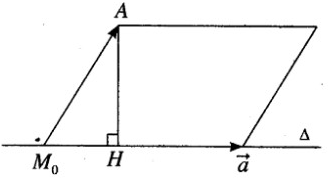
Tính khoảng cách từ điểm A(1; 0; 1) đến đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{y}{2} = \dfrac{z}{1}\)
Phương pháp giải
Sử dụng công thức tính khoảng cách từ một điểm đến đường thẳng: \(d\left( {{M_0},\Delta } \right) = \dfrac{{\left| {\left[ {\overrightarrow {{u_\Delta }} ,\overrightarrow {{M_0}A} } \right]} \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|}}\)
Hướng dẫn giải
Đường thẳng \(\Delta\) đi qua điểm M0(1; 0; 0) và có vecto chỉ phương \(\overrightarrow u = (2;2;1)\)
Ta có \(\overrightarrow {{M_0}A} = (0;0;1), \overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow {{M_0}A} } \right] = (2; - 2;0)\)
\(d(A,\Delta ) = \dfrac{{|\overrightarrow n |}}{{|\overrightarrow u |}} = \dfrac{{\sqrt {4 + 4 + 0} }}{{\sqrt {4 + 4 + 1} }} = \dfrac{{2\sqrt 2 }}{3}\)
Vậy khoảng cách từ điểm A đến \(\Delta\) là \(\dfrac{{2\sqrt 2 }}{3}\)
7. Giải bài 3.37 trang 131 SBT Hình học 12
Cho đường thẳng \(\Delta :\dfrac{{x + 3}}{2} = \dfrac{{y + 1}}{3} = \dfrac{{z + 1}}{2}\,\, và\,\, mặt\,\, phẳng \,\,(\alpha ): 2x – 2y + z + 3 = 0\)
a) Chứng minh rằng Δ song song với (α).
b) Tính khoảng cách giữa Δ và (α)
Phương pháp giải
- Sử dụng điều kiện đường thẳng \(\Delta\) song song với mặt phẳng \(\left( \alpha \right): \left\{ \begin{array}{l}\overrightarrow {{u_\Delta }} .\overrightarrow {{n_{\left( \alpha \right)}}} = 0\\M \in \Delta ,M \notin \left( \alpha \right)\end{array} \right.\)
- Sử dụng công thức tính khoảng cách \(d\left( {\Delta ,\left( \alpha \right)} \right) = d\left( {M,\left( \alpha \right)} \right) = \dfrac{{\left| {\left[ {\overrightarrow {MA} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\)
Hướng dẫn giải
a) Ta có: \(\overrightarrow {{u_\Delta }} = (2;3;2)\) và \(\overrightarrow {{n_\alpha }} = (2; - 2;1)\)
\(\overrightarrow {{u_\Delta }} .\overrightarrow {{n_\alpha }} = 4 - 6 + 2 = 0\) (1)
Xét điểm M0(-3; -1; -1) thuộc \(\Delta\), ta thấy tọa độ M0 không thỏa mãn phương trình của \((\alpha )\). Vậy \({M_0} \notin (\alpha )\) (2).
Từ (1) và (2) ta suy ra \(\Delta //(\alpha )\)
b) \(d(\Delta ,(\alpha )) = d({M_0},(\alpha )) = \dfrac{{|2.( - 3) - 2.( - 1) + ( - 1) + 3|}}{{\sqrt {4 + 4 + 1} }} = \dfrac{2}{3}\)
Vậy khoảng cách giữa đường thẳng \(\Delta\) và mặt phẳng \((\alpha )\) là \(\dfrac{2}{3}\)
8. Giải bài 3.38 trang 131 SBT Hình học 12
Tính khoảng cách giữa các cặp đường thẳng \(\Delta\) và \(\Delta '\) trong các trường hợp sau:
a) \(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = - 1 - t}\\{z = 1}\end{array}} \right.\,\, và \,\, \Delta ':\left\{ {\begin{array}{*{20}{c}}{x = 2 - 3t'}\\{y = 2 + 3t'}\\{z = 3t'}\end{array}} \right.\)
b) \(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = 4 - t}\\{z = - 1 + 2t}\end{array}} \right. \,\, và \,\, \Delta ':\left\{ {\begin{array}{*{20}{c}}{x = t'}\\{y = 2 - 3t'}\\{z = - 3t'}\end{array}} \right.\)
Phương pháp giải
- Viết phương trình mặt phẳng chứa một đường thẳng và song song với đường thẳng còn lại.
- Tính khoảng cách giữa hai đường thẳng chéo nhau, sử dụng công thức:
\(d\left( {\Delta ,\Delta '} \right) = d\left( {\Delta ,\left( \alpha \right)} \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c{z_0} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Ở đó \(\Delta ' \subset \left( \alpha \right),\Delta //\left( \alpha \right)\) và \(M \in \Delta\)
Hướng dẫn giải
a) Gọi \((\alpha)\) là mặt phẳng chứa \(\Delta\) và song song với \(\Delta '\)
Hai vecto có giá song song hoặc nằm trên \((\alpha )\) là: \(\overrightarrow u = (1; - 1;0)\) và \(\overrightarrow u ' = ( - 1;1;1)\)
Suy ra \(\overrightarrow {{n_\alpha }} = \left[ {\overrightarrow {u'} ,\overrightarrow u } \right] = \left( { - 1; - 1;0} \right)\)
\((\alpha )\) đi qua điểm M1(1; -1; 1) thuộc \(\Delta\) và có vecto pháp tuyến: \(\overrightarrow {{n_{\alpha '}}} = (1;1;0)\)
Vậy phưong trình của mặt phẳng \((\alpha )\) có dạng x – 1 + y + 1=0 hay x + y = 0
Ta có: M2(2; 2; 0) thuộc đường thẳng \(\Delta '\)
\(d(\Delta ,\Delta ') = d({M_2},(\alpha )) = \dfrac{{|2 + 2|}}{{\sqrt {1 + 1} }} = 2\sqrt 2 \)
b) Hai đường thẳng \(\Delta \) và \(\Delta '\) có phương trình là:
\(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = 4 - t}\\{z = - 1 + 2t}\end{array}} \right.\) và \(\Delta ':\left\{ {\begin{array}{*{20}{c}}{x = t'}\\{y = 2 - 3t'}\\{z = - 3t'}\end{array}} \right.\)
Phương trình mặt phẳng \((\alpha )\) chứa \(\Delta \) và song song với \(\Delta '\) là 9x + 5y – 2z – 22 = 0
Lấy điểm M’(0; 2; 0) trên \(\Delta '\)
Ta có \(d(\Delta ,\Delta ') = d(M',(\alpha )) = \dfrac{{|5.(2) - 22|}}{{\sqrt {81 + 25 + 4} }} = \dfrac{{12}}{{\sqrt {110} }}\)
Vậy khoảng cách giữa hai đường thẳng \(\Delta\) và \(\Delta '\) là \(\dfrac{{12}}{{\sqrt {110} }}\)
9. Giải bài 3.39 trang 131 SBT Hình học 12
Cho hai đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y + 3}}{1} = \dfrac{{z - 4}}{{ - 2}} \,\, và \,\, \Delta ':\dfrac{{x + 2}}{{ - 4}} = \dfrac{{y - 1}}{{ - 2}} = \dfrac{{z + 1}}{4}\)
a) Xét vị trí tương đối giữa Δ và Δ′
b) Tính khoảng cách giữa Δ và Δ′
Phương pháp giải
a) Nhận xét vị trí tương đối của hai đường thẳng, sử dụng mối quan hệ giữa hai đường thẳng song song: \(\Delta //\Delta ' \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u = k\overrightarrow {u'} \\M \in \Delta ,M \notin \Delta '\end{array} \right.\)
b) Khoảng cách giữa hai đường thẳng song song \(d\left( {\Delta ,\Delta '} \right) = d\left( {M,\Delta '} \right) = \dfrac{{\left| {\left[ {\overrightarrow {MA'} ,\overrightarrow {u'} } \right]} \right|}}{{\left| {\overrightarrow {u'} } \right|}}\)
Hướng dẫn giải
a) \(\Delta\) đi qua điểm M0(1; -3; 4) và có vecto chỉ phương \(\overrightarrow a = (2;1; - 2)\)
\(\Delta '\) đi qua điểm M0’ (-2; 1; -1) và có vecto chỉ phương \(\overrightarrow {a'} = ( - 4; - 2;4)\)
Ta có \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {a'} = 2\overrightarrow a }\\{{M_0} \notin \Delta '}\end{array}} \right.\)
Vậy \(\Delta '\) song song với \(\Delta\)
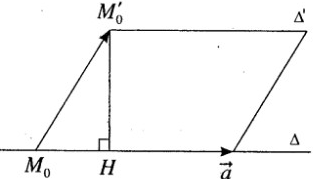
b) Ta có \(\overrightarrow {{M_0}M{'_0}} = ( - 3;4; - 5), \overrightarrow a = (2;1; - 2)\)
\(\overrightarrow n = \left[ {\overrightarrow {{M_0}M{'_0}} ,\overrightarrow a } \right] = ( - 3; - 16; - 11)\)
\(d(\Delta ,\Delta ') = M{'_0}H = \dfrac{{|\overrightarrow n |}}{{|\overrightarrow a |}} = \dfrac{{\sqrt {9 + 256 + 121} }}{{\sqrt {4 + 1 + 4} }} = \dfrac{{\sqrt {386} }}{3}\)
10. Giải bài 3.40 trang 131 SBT Hình học 12
Cho điểm M(2; -1; 1) và đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{2}\)
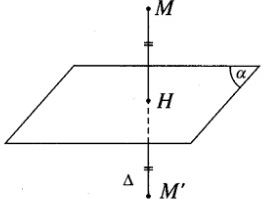
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên đường thẳng Δ;
b) Tìm tọa độ điểm M’ đối xứng với M qua đường thẳng Δ.
Phương pháp giải
a) Tham số hóa tọa độ hình chiếu của M trên \(\Delta\)
Lập phương trình tìm tham số, sử dụng điều kiện \(\overrightarrow {MH} \bot \overrightarrow {{u_\Delta }}\)
b) M' đối xứng với M qua \(\Delta\) nếu H là trung điểm của \(MM'\)
Hướng dẫn giải
a) Phương trình tham số của \(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = - 1 - t}\\{z = 2t}\end{array}} \right.\)
Xét điểm \(H(1 + 2t; - 1 - t;2t) \in \Delta\)
Ta có \(\overrightarrow {MH} = (2t - 1; - t;2t - 1), \overrightarrow {{u_\Delta }} = (2; - 1;2)\)
H là hình chiếu vuông góc của M trên \(\Delta \Leftrightarrow \overrightarrow {MH} .\overrightarrow {{u_\Delta }} = 0\)
\(\Leftrightarrow 2(2t - 1) + t + 2(2t - 1) = 0 \Leftrightarrow t = \dfrac{4}{9}\)
Ta suy ra tọa độ điểm \(H\left( {\dfrac{{17}}{9};\dfrac{{ - 13}}{9};\dfrac{8}{9}} \right)\)
b) H là trung điểm của MM’, suy ra \({x_{M'}} + {x_M} = 2{x_H}\)
Suy ra \({x_{M'}} = 2{x_H} - {x_M} = \dfrac{{34}}{9} - 2 = \dfrac{{16}}{9}\)
Tương tự, ta được
\({y_{M'}} = 2{y_H} - {y_M} = \dfrac{{ - 26}}{9} + 1 = \dfrac{{ - 17}}{9};\)\({z_{M'}} = 2{z_H} - {z_M} = \dfrac{{16}}{9} - 1 = \dfrac{7}{9}\)
Vậy \(M'\left( {\dfrac{{16}}{9};\dfrac{{ - 17}}{9};\dfrac{7}{9}} \right)\)
11. Giải bài 3.41 trang 132 SBT Hình học 12
Cho điểm M(1; -1; 2) và mặt phẳng (α): 2x – y + 2z + 12 = 0
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α)
b) Tìm tọa độ điểm M’ đối xứng với M qua mặt phẳng (α) .
Phương pháp giải
a)
- Viết phương trình tham số của đường thẳng \(\Delta\) đi qua M và vuông góc \(\left( \alpha \right)\)
- Tìm giao điểm của \(\Delta\) và \(\left( \alpha \right)\)
b) M' đối xứng với M qua \(\left( \alpha \right) \Leftrightarrow H\) là trung điểm của MM'
Hướng dẫn giải
a)
Phương trình tham số của đường thẳng \(\Delta\) đi qua điểm M(1; -1; 2) và vuông góc với mặt phẳng \((\alpha ) : 2x – y + 2z + 12 = 0\) là: \(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = - 1 - t}\\{z = 2 + 2t}\end{array}} \right.\)
Xét điểm H(1 + 2t; -1 – t ; 2 + 2t) \(\in \Delta \)
Ta có \(H \in (\alpha ) \Leftrightarrow 2(1 + 2t) + (1 + t) + 2(2 + 2t) + 12 = 0 \Leftrightarrow t = \dfrac{{ - 19}}{9}\)
Vậy ta được \(H\left( {\dfrac{{ - 29}}{9};\dfrac{{10}}{9};\dfrac{{ - 20}}{9}} \right)\)
b) H là trung điểm của MM’, suy ra \({x_{M'}} = 2{x_H} - {x_M} = \dfrac{{ - 58}}{9} - 1 = \dfrac{{ - 67}}{9}\)
\({y_{M'}} = 2{y_H} - {y_M} = \dfrac{{20}}{9} + 1 = \dfrac{{29}}{9}\)
\({z_{M'}} = 2{z_H} - {z_M} = \dfrac{{ - 40}}{9} - 2 = \dfrac{{ - 58}}{9}\)
Vậy ta được \(M'\left( {\dfrac{{ - 67}}{9};\dfrac{{29}}{9};\dfrac{{ - 58}}{9}} \right)\)
12. Giải bài 3.42 trang 132 SBT Hình học 12
Cho hai đường thẳng: \(d:\dfrac{{x - 1}}{{ - 1}} = \dfrac{{y - 2}}{2} = \dfrac{z}{3} \,\, và \,\, d':\left\{ {\begin{array}{*{20}{c}}{x = 1 + t'}\\{y = 3 - 2t'}\\{z = 1}\end{array}} \right.\)
Lập phương trình đường vuông góc chung của d và d’.
Phương pháp giải
- Tham số hóa tọa độ hai điểm M, M' lần lượt thuộc hai đường thẳng d, d'.
- Sử dụng điều kiện \(\overrightarrow {MM'}\) là đường vuông góc chung của d, d' thì \(\left\{ \begin{array}{l}\overrightarrow {MM'} .\overrightarrow {{u_d}} = 0\\\overrightarrow {MM'} .\overrightarrow {{u_{d'}}} = 0\end{array} \right.\)
- Tìm tọa độ của M, M' và viết phương trình đường thẳng MM'.
Hướng dẫn giải
Phương trình tham số của đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 1 - t}\\{y = 2 + 2t}\\{z = 3t}\end{array}} \right.\)
Vecto chỉ phương của hai đường thẳng d và d’ lần lượt là \(\overrightarrow a = ( - 1;2;3),\overrightarrow {a'} = (1; - 2;0)\)
Xét điểm M(1 – t; 2 + 2t; 3t) trên d và điểm M’(1 + t’; 3 – 2t’ ; 1) trên d’ ta có \(\overrightarrow {MM'} = (t' + t;1 - 2t' - 2t;1 - 3t)\)
MM’ là đường vuông góc chung của d và d’.
\(\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {MM'} .\overrightarrow a = 0}\\{\overrightarrow {MM'} .\overrightarrow {a'} = 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - t' - t + 2 - 4t' - 4t + 3 - 9t = 0\\t' + t - 2 + 4t' + 4t = 0\end{array} \right.\)
\(\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5t' + 14t = 5}\\{5t' + 5t = 2}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{t = \dfrac{1}{3}}\\{t' = \dfrac{1}{{15}}}\end{array}} \right.\)
Thay giá trị của t và t’ vào ta được tọa độ M và M’ là \(M\left( {\dfrac{2}{3};\dfrac{8}{3};1} \right),M'\left( {\dfrac{{16}}{{15}};\dfrac{{43}}{{15}};1} \right)\)
Do đó \(\overrightarrow {MM'} = \left( {\dfrac{6}{{15}};\dfrac{3}{{15}};0} \right)\)
Suy ra đường vuông góc chung \(\Delta \) của d và d’ có vecto chỉ phương \(\overrightarrow u = (2;1;0)\)
Vậy phương trình tham số của \(\Delta \) là: \(\left\{ {\begin{array}{*{20}{c}}{x = \dfrac{2}{3} + 2t}\\{y = \dfrac{8}{3} + t}\\{z = 1}\end{array}} \right.\)
13. Giải bài 3.43 trang 132 SBT Hình học 12
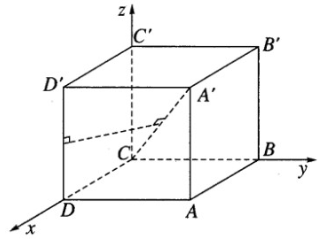
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Bằng phương pháp tọa độ hãy tính khoảng cách giữa hai đường thẳng CA’ và DD’.
Phương pháp giải
- Chọn hệ trục tọa độ gốc \(C\left( {0;0;0} \right)\) và xác định tọa độ các điểm còn lại.
- Viết phương trình mặt phẳng chứa CA' và song song DD'.
- Tính khoảng cách \(d\left( {CA',DD'} \right) = d\left( {DD',\left( \alpha \right)} \right) = d\left( {D,\left( \alpha \right)} \right)\)
Hướng dẫn giải
Ta chọn hệ trục tọa độ sao cho: C là gốc tọa độ, \(\overrightarrow {CD} = a\overrightarrow i ;\overrightarrow {CB} = a\overrightarrow j ;\overrightarrow {CC'} = a\overrightarrow k \)
Trong hệ tọa độ vừa chọn ta có: C(0; 0; 0), A’(a; a ; a), D(a; 0;0), D’(a; 0; a)
\(\overrightarrow {CA'} = (a;a;a),\overrightarrow {{\rm{DD}}'} = (0;0;a)\)
Gọi \((\alpha )\) là mặt phẳng chứa \(\overrightarrow {CA'} \) và song song với \(\overrightarrow {DD'}\)
Mặt phẳng \((\alpha)\) có vecto pháp tuyến là: \(\overrightarrow n = \left[ {\overrightarrow {CA'} ,\overrightarrow {{\rm{DD}}'} } \right] = ({a^2}; - {a^2};0)\) hay x – y = 0
Phương trình tổng quát của \((\alpha )\) là x – y = 0.
Ta có: \(d\left( {CA',DD'} \right) = d\left( {D,\left( \alpha \right)} \right)= \dfrac{{\left| { - a} \right|}}{{\sqrt {1 + 1 + 0} }} = \dfrac{a}{{\sqrt 2 }}\)
14. Giải bài 3.44 trang 132 SBT Hình học 12
Cho mặt phẳng (α) : 2x + y + z – 1 = 0 và đường thẳng \(d: \dfrac{{x - 1}}{2} = \dfrac{y}{1} = \dfrac{{z + 2}}{{ - 3}}\)
Gọi M là giao điểm của d và (α), hãy viết phương trình của đường thẳng Δ đi qua M vuông góc với d và nằm trong (α)
Phương pháp giải
- Tìm giao điểm của d và \(\left( \alpha \right)\)
- Đường thẳng \(\Delta\) vuông góc với d và nằm trong \(\left( \alpha \right) \Rightarrow \overrightarrow {{u_\Delta }} = \left[ {\overrightarrow {{u_d}} ,\overrightarrow {{n_{\left( \alpha \right)}}} } \right]\)
Hướng dẫn giải
Phương trình tham số của đường thẳng d: \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = t}\\{z = - 2 - 3t}\end{array}} \right.\)
Xét phương trình \(2(1 + 2t) + t + ( - 2 – 3t) – 1 = 0\) \( \Leftrightarrow 2t - 1 = 0\) \( \Leftrightarrow t = \dfrac{1}{2}\)
Vậy đưởng thẳng d cắt mặt phẳng \(\alpha\) tại điểm \(M\left( {2;\dfrac{1}{2}; - \dfrac{7}{2}} \right)\)
Ta có vecto pháp tuyến của mặt phẳng \((\alpha )\) và vecto chỉ phương của đường thẳng d lần lượt là \(\overrightarrow {{n_\alpha }} = (2;1;1) \,\, và \,\, \overrightarrow {{u_d}} = (2;1; - 3)\)
Gọi \(\overrightarrow {{u_\Delta }}\) là vecto pháp tuyến của \(\Delta\), ta có \(\overrightarrow {{u_\Delta }} \bot \overrightarrow {{n_\alpha }} \,\, và \,\, \overrightarrow {{u_\Delta }} \bot \overrightarrow {{u_d}}\)
Ta có: \(\left[ {\overrightarrow {{n_\alpha }} ,\overrightarrow {{u_d}} } \right] = \left( { - 4;8;0} \right)\) nên chọn \(\overrightarrow {{u_\Delta }} = \left( {1; - 2;0} \right)\)
Vậy phương trình tham số của \(\Delta\) là \(\left\{ {\begin{array}{*{20}{c}}{x = 2 + t}\\{y = \dfrac{1}{2} - 2t}\\{z = - \dfrac{7}{2}}\end{array}} \right.\)
15. Giải bài 3.45 trang 132 SBT Hình học 12
Cho hai đường thẳng d1: \(\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{{ - 3}} = \dfrac{{z - 5}}{4} \,\, và \,\,d2: \left\{ {\begin{array}{*{20}{c}}{x = 7 + 3t}\\{y = 2 + 2t}\\{z = 1 - 2t}\end{array}} \right.\)
a) Chứng minh rằng d1 và d2 cùng nằm trong một mặt phẳng (α).
b) Viết phương trình của (α).
Phương pháp giải
Sử dụng vị trí tương đối giữa hai đường thẳng
Cho đường thẳng ∆1 qua điểm M1 và có vec tơ chỉ phương \(\overrightarrow{u_{1}}\), đường thẳng ∆2 qua điểm M2 và có vec tơ chỉ phương \(\overrightarrow{u_{2}}\)
* ∆1 và ∆2 chéo nhau ⇔ ∆1 và ∆2 không nằm trong cùng một mặt phẳng ⇔ \(\left [\overrightarrow{u_{1}},\overrightarrow{u_{2}} \right ]\overrightarrow{M_{1}M_{2}}\neq 0\)
* ∆1 và ∆2 song song ⇔ \(\left\{\begin{matrix} \overrightarrow{u_{1}}=k\overrightarrow{u_{2}}\\ M_{1}\in \Delta _{1}\\ M_{2}\notin \Delta _{2} \end{matrix}\right.\)
* ∆1 trùng với ∆2 ⇔ \(\overrightarrow{u_{1}}, \overrightarrow{u_{2}}, \overrightarrow{M_{1}M_{2}}\) là ba vectơ cùng phương.
* ∆1 cắt ∆2 ⇔ \(\overrightarrow{u_{1}},\overrightarrow{u_{2}}\) không cùng phương và \(\left [\overrightarrow{u_{1}},\overrightarrow{u_{2}} \right ]\overrightarrow{M_{1}M_{2}}= 0\)
Hướng dẫn giải
a) Ta có \(\overrightarrow {{u_{{d_1}}}} = \left( {2; - 3;4} \right) \,\, và \,\, \overrightarrow {{u_{{d_2}}}} = (3;2; - 2)\)
\(\overrightarrow n = \left[ {\overrightarrow {{u_{{d_1}}}} ,\overrightarrow {{u_{{d_2}}}} } \right] = ( - 2;16;13)\)
Lấy điểm M1(1; -2; 5) trên d1 và điểm M2(7;2;1) trên d2.
Ta có \(\overrightarrow {{M_1}{M_2}} = (6;4; - 4); \overrightarrow n .\overrightarrow {{M_1}{M_2}} = - 12 + 64 - 52 = 0\)
Suy ra \({d_1}\) và \({d_2}\) cùng nằm trong mặt phẳng \((\alpha )\)
b) Mặt phẳng \((\alpha )\) chứa \({M_1}\) và có vecto pháp tuyến là \(\overrightarrow n \), vậy phương trình của \((\alpha )\) là:
\(– 2(x – 1) +16(y + 2) + 13(z – 5) = 0 \,\, hay \,\, 2x – 16y – 13z + 31 = 0\)
Các em hãy luyện tập bài trắc nghiệm Phương trình đường thẳng Toán 12 sau để nắm rõ thêm kiến thức bài học.
Tham khảo thêm
- doc Giải bài tập SBT Toán 12 Bài 1: Hệ tọa độ trong không gian
- doc Giải bài tập SBT Toán 12 Bài 2: Phương trình mặt phẳng