Giải bài tập SBT Toán 12 Bài 1: Hệ tọa độ trong không gian

Trong không gian Oxyz cho ba vecto \(\overrightarrow a = (2; - 1;2),\overrightarrow b = (3;0;1),\overrightarrow c = ( - 4;1; - 1)\). Tìm tọa độ của các vecto \(\overrightarrow m \) và \(\overrightarrow n\) biết rằng:

a) \(\overrightarrow m = 3\overrightarrow a - 2\overrightarrow b + \overrightarrow c \)

b) \(\overrightarrow n = 2\overrightarrow a + \overrightarrow b + 4\overrightarrow c\)

Phương pháp giải

Sử dụng công thức \(k\overrightarrow a \pm l\overrightarrow b = \left( {kx \pm lx';ky \pm ly';kz \pm lz'} \right)\)

Hướng dẫn giải

a) Ta có: \(\overrightarrow m = 3\overrightarrow a - 2\overrightarrow b + \overrightarrow c = ( - 4; - 2;3)\)

b) \(\overrightarrow n = 2\overrightarrow a + \overrightarrow b + 4\overrightarrow c = ( - 9;2;1)\)

Trong không gian Oxyz cho vecto \(\overrightarrow a = (1; - 3;4)\)

a) Tìm y₀ và z₀ để cho vecto \(\overrightarrow b = (2;{y_0};{z_0})\) cùng phương với \(\overrightarrow a\)

b) Tìm tọa độ của vecto \(\overrightarrow c \) biết rằng  \(\overrightarrow a \) và \(\overrightarrow c\) ngược hướng và \(|\overrightarrow {c|} = 2|\overrightarrow a |\)

Phương pháp giải

Sử dụng lý thuyết: \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương khi và chỉ khi \(\overrightarrow a = k\overrightarrow b\) với k là một số thực.

Hướng dẫn giải

a) Ta biết rằng \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương khi và chỉ khi  \(\overrightarrow a = k\overrightarrow b\) với k là một số thực.

Theo giả thiết ta có: \(\overrightarrow b = ({x_0};{y_0};{z_0})\) với x₀ = 2. Ta suy ra \(k = \dfrac{1}{2}\) nghĩa là \(l = \dfrac{1}{2}{x_0}\)

Do đó: \(- 3 = \dfrac{1}{2}{y_0}\) nên y₀ = -6

\(4 = \dfrac{1}{2}{z_0}\) nên z₀ = 8

Vậy ta có \(\overrightarrow b = (2; - 6;8)\)

b) Theo giả thiết ta có \(\overrightarrow c = - 2\overrightarrow a \)

Do đó tọa độ của \(\overrightarrow c \) là: \(\overrightarrow c = \left( { - 2;6; - 8} \right)\)

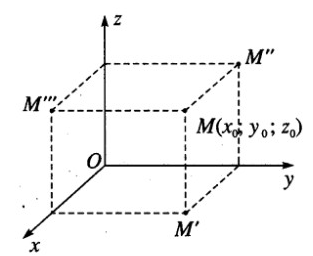
Trong không gian Oxyz cho điểm M có tọa độ (x₀; y₀ ; z₀). Tìm tọa độ hình chiếu vuông góc của điểm M trên các mặt phẳng  tọa độ (Oxy), (Oyz), (Ozx).

Phương pháp giải

Dựng hình chiếu của M trên các mặt phẳng tọa độ và tìm tọa độ các hình chiếu đó.

Hướng dẫn giải

Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).

Ta có: M’(x₀; y₀; 0), M’’ (0; y₀; z₀), M’’’(x₀; 0; z₀).

Cho hai bộ ba điểm:

a) A = (1; 3; 1), B = (0; 1; 2), C = (0; 0; 1)

b) M = (1; 1; 1), N = (-4; 3; 1), P = (-9; 5; 1)

Hỏi bộ nào có ba điểm thẳng hàng?

Phương pháp giải

Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto \(\overrightarrow {AB}\)  và \(\overrightarrow {AC}\) cùng phương

Hướng dẫn giải

a) Ta có  \(\overrightarrow {AB} = ( - 1; - 2;1), \overrightarrow {AC} = ( - 1; - 3;0)\)

Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto \(\overrightarrow {AB}\)  và \(\overrightarrow {AC}\) cùng phương, nghĩa là \(\overrightarrow {AB} = k\overrightarrow {AC} \) với k là một số thực.

Giả sử ta có \(\overrightarrow {AB} = k\overrightarrow {AC}\), khi đó \(\left\{ {\begin{array}{*{20}{c}}{k.( - 1) = - 1}\\{k.( - 3) = - 2}\\{k.(0) = 1}\end{array}} \right.\)

Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên.

Vậy ba điểm A, B, C không thẳng hàng.

b) Ta có: \(\overrightarrow {MN} = ( - 5;2;0)\,\, và \,\,\overrightarrow {MP} = ( - 10;4;0)\). Hai vecto \(\overrightarrow {MN}\) và \(\overrightarrow {MP}\) thỏa mãn điều kiện: \(\overrightarrow {MN} = k\overrightarrow {MP}\) với \(k = \dfrac{1}{2}\) nên ba điểm M, N, P thẳng hàng.

Trong không gian Oxyz, hãy tìm trên mặt phẳng (Oxz) một điểm M cách đều ba điểm A(1; 1; 1), B(-1; 1; 0), C(3; 1; -1).

Phương pháp giải

- Gọi tọa độ của \(M \in \left( {Oxz} \right)\). Tính khoảng cách MA, MB, MC.

- Lập hệ phương trình, giải hệ và kết luận.

Hướng dẫn giải

Điểm M thuộc mặt phẳng (Oxz) có tọa độ là (x; 0; z), cần phải tìm x và z. Ta có:

MA² = (1 – x)² + 1 + (1 – z)²

MB² = (–1 – x)² + 1 + z²

MC² = (3 – x)² + 1 + (–1 – z)²

Theo giả thiết M cách đều ba điểm A, B, C nên ta có  MA² = MB² = MC²

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} {\left( {1 - x} \right)^2} + 1 + {\left( {1 - z} \right)^2} = {\left( { - 1 - x} \right)^2} + 1 + {z^2}\\ {\left( {1 - x} \right)^2} + 1 + {\left( {1 - z} \right)^2} = {\left( {3 - x} \right)^2} + 1 + {\left( { - 1 - z} \right)^2} \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 2x + 1 - 2z = 2x\\ 1 - 2x - 2z = 9 - 6x + 2z \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 4x - 2z + 1 = 0\\ 4x - 4z - 8 = 0 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x = \dfrac{5}{6}\\ z = - \dfrac{7}{6} \end{array} \right. \Rightarrow M\left( {\dfrac{5}{6};0; - \dfrac{7}{6}} \right) \end{array}\)

Cho hình tứ diện ABCD. Chứng minh rằng:

a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overline {BC}\)

b) \(\overrightarrow {AB} = \dfrac{1}{2}\overrightarrow {AC} + \dfrac{1}{2}\overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {CD} + \overrightarrow {DB}\)

Phương pháp giải

Xen điểm thích hợp chứng minh đẳng thức véc tơ.

Hướng dẫn giải

a) Ta có: \(\overrightarrow {AC} = \overrightarrow {AD} + \overrightarrow {DC}\)

\(\overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {CD}\)

Do đó: \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC} \,\, vì \,\,\overrightarrow {DC} = - \overrightarrow {CD}\)

b) Vì \(\overrightarrow {AB} = \overrightarrow {AD} + \overrightarrow {DB} \,\, và \,\,\overrightarrow {AD} = \overrightarrow {AC} + \overrightarrow {CD} \,\, nên \,\,\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CD} + \overrightarrow {DB} \)

Do đó: \(2\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {AD} + \overrightarrow {CD} + 2\overrightarrow {DB}\)

Vậy \(\overrightarrow {AB} = \dfrac{1}{2}\overrightarrow {AC} + \dfrac{1}{2}\overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {CD} + \overrightarrow {DB}\)

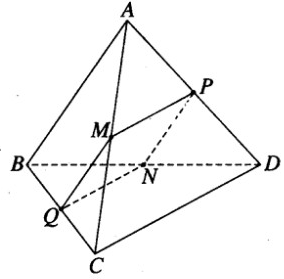
Cho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng:

a) \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} = 2\overrightarrow {MN}\)

b) \(\overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} - \overrightarrow {BD} = 2\overrightarrow {PQ}\)

Phương pháp giải

Xen điểm thích hợp chứng minh đẳng thức véc tơ.

Hướng dẫn giải

a) Ta có  MPNQ là hình bình hành vì  \(\overrightarrow {MP} = \overrightarrow {QN} = \dfrac{1}{2}\overrightarrow {CD}\) và \(\overrightarrow {MQ} = \overrightarrow {PN} = \dfrac{1}{2}\overrightarrow {AB}\)

Do đó \(\overrightarrow {MN} = \overrightarrow {MQ} + \overrightarrow {MP} = \dfrac{{\overrightarrow {AB} }}{2} + \dfrac{{\overrightarrow {CD} }}{2}\)  hay  \(2\overrightarrow {MN} = \overrightarrow {AB} + \overrightarrow {CD}\)      (1)

Mặt khác \(\overrightarrow {AB} = \overrightarrow {AD} + \overrightarrow {DB}\)

\(\overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {BD}\)

Nên \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB}\)          (2)

Vì \(\overrightarrow {DB} = - \overrightarrow {BD}\)

Từ (1) và (2) ta có: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} = 2\overrightarrow {MN} \)  là đẳng thức cần chứng minh.

b) Ta có: \(\overrightarrow {PQ} = \overrightarrow {MQ} - \overrightarrow {MP} = \dfrac{{\overrightarrow {AB} }}{2} - \dfrac{{\overrightarrow {CD} }}{2}\)

Do đó: \(2\overrightarrow {PQ} = \overrightarrow {AB} - \overrightarrow {CD}\)   (3)

Mặt khác: \(\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB}\)

\(\overrightarrow {CD} = \overrightarrow {BD} - \overrightarrow {BC} \)

Nên \(\overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} - \overrightarrow {BD}\)    (4)

Vì \(\overrightarrow {CB} - ( - \overrightarrow {BC} ) = \overrightarrow 0 \)

Từ (3) và (4) ta suy ra \(\overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} - \overrightarrow {BD} = 2\overrightarrow {PQ}\) là đẳng thức cần chứng minh.

Trong không gian cho ba vecto tùy ý  \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\).

Gọi 

\(\overrightarrow u = \overrightarrow a - 2\overrightarrow b ,\) \(\overrightarrow v = 3\overrightarrow b - \overrightarrow c ,\) \(\overrightarrow {\rm{w}} = 2\overrightarrow c - 3\overrightarrow a \)

Chứng tỏ rằng ba vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow {\rm{w}}\) đồng phẳng.

Phương pháp giải

Muốn chứng tỏ rằng ba vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow {\rm{w}}\) đồng phẳng ta cần tìm hai số thực p và q sao cho \(\overrightarrow {\rm{w}} = p\overrightarrow u + q\overrightarrow v\)

Hướng dẫn giải

Giả sử có \(\overrightarrow {\rm{w}} = p\overrightarrow u + q\overrightarrow v \)

\(2\overrightarrow c - 3\overrightarrow a = p(\overrightarrow a - 2\overrightarrow b ) + q(3\overrightarrow b - \overrightarrow c )\)

\(\Leftrightarrow (3 + p)\overrightarrow a + (3q - 2p)\overrightarrow b - (q + 2)\overrightarrow c = \overrightarrow 0\)  (1)

Vì ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\) lấy tùy ý  nên đẳng thức (1) xảy ra khi và chỉ khi:

\(\left\{ {\begin{array}{*{20}{c}}{3 + p = 0}\\{3q - 2p = 0}\\{q + 2 = 0}\end{array}} \right. \) \( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{p = - 3}\\{q = - 2}\end{array}} \right.\)

Như vậy ta có: \(\overrightarrow {\rm{w}} = - 3\overrightarrow u - 2\overrightarrow v\)  nên ba vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow {\rm{w}} \) đồng phẳng.

Trong không gian Oxyz cho một vecto \(\overrightarrow a\) tùy ý khác vecto\(\overrightarrow 0\). Gọi \(\alpha ,\beta ,\gamma\) là ba góc tạo bởi ba vecto đơn vị \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k\) trên ba trục Ox, Oy, Oz và vecto \(\overrightarrow a\). Chứng minh rằng:  \({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1\)

Phương pháp giải

- Dựng véc tơ đơn vị \(\overrightarrow {{a_0}}\) cùng hướng với vecto \(\overrightarrow a\)

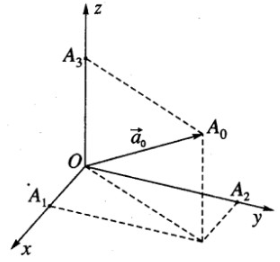
- Dựng điểm A₀ sao cho \(\overrightarrow {O{A_0}} = \overrightarrow {{a_0}}\) và các điểm \({A_1},{A_2},{A_3}\) lần lượt là hình chiếu của \({A_0}\) lên các trục tọa độ.

- Tính \(\cos \alpha ,\cos \beta ,\cos \gamma\) và suy ra điều phải chứng minh.

Hướng dẫn giải

Gọi \(\overrightarrow {{a_0}} \) là vecto đơn vị cùng hướng với vecto \(\overrightarrow a\), ta có \(\overrightarrow {{a_0}} = \dfrac{1}{{|\overrightarrow a |}}\overrightarrow a\)

Gọi \(\overrightarrow {O{A_0}} = \overrightarrow {{a_0}}\) và các điểm A₁, A₂, A₃ theo thứ tự là hình chiếu vuông góc của điểm A₀ trên các trục Ox, Oy, Oz.

Khi đó ta có:  \(\dfrac{{|\overrightarrow {O{A_1}} |}}{{|\overrightarrow {O{A_0}} |}} = \cos \alpha ,\dfrac{{|\overrightarrow {O{A_2}} |}}{{|\overrightarrow {O{A_0}|} }} = \cos \beta ,\dfrac{{|\overrightarrow {O{A_3}} |}}{{|\overrightarrow {O{A_0}} |}} = \cos \gamma \)

Vì  \(|\overrightarrow {O{A_0}} | = 1\) nên \(|\overrightarrow {O{A_1}} | = \cos \alpha ,|\overrightarrow {O{A_2}} | = \cos \beta ,|\overrightarrow {O{A_3}} | = \cos \gamma \)

Ta có \(\overrightarrow {O{A_0}} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} + \overrightarrow {O{A_3}} \)  , ta suy ra:  \(\overrightarrow {O{A_0}} = \cos \alpha \overrightarrow i + \cos \beta \overrightarrow j + \cos \gamma \overrightarrow k \,\, hay \,\,\overrightarrow {O{A_0}} = (\cos \alpha ;\cos \beta ;\cos \gamma\)

Vì  \(\overrightarrow {O{A_0}} = \overrightarrow {{a_0}} \)  mà \(|\overrightarrow {{a_0}} | = 1\) nên ta có: \({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1\)

Cho hình tứ diện ABCD.

a) Chứng minh hệ thức: \(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\)

b) Từ hệ thức trên hãy suy ra định lí: “Nếu một hình tứ diện có hai cặp cạnh đối diện vuông góc với nhau thì cặp cạnh đối diện thứ ba cũng vuông góc với nhau.”

Phương pháp giải

- Xen điểm thích hợp vào từng cặp tích vô hướng.

- Cộng các tích vô hướng và suy ra điều phải chứng minh.

Hướng dẫn giải

a) Ta có \(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} (\overrightarrow {AD} - \overrightarrow {AC} ) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \)  (1)

\(\overrightarrow {AC} .\overrightarrow {DB} = \overrightarrow {AC} (\overrightarrow {AB} - \overrightarrow {AD} ) = \overrightarrow {AC} .\overrightarrow {AB} - \overrightarrow {AC} .\overrightarrow {AD}\)   (2)

\(\overrightarrow {AD} .\overrightarrow {BC} = \overrightarrow {AD} (\overrightarrow {AC} - \overrightarrow {AB} ) = \overrightarrow {AD} .\overrightarrow {AC} - \overrightarrow {AD} .\overrightarrow {AB} \)    (3)

Lấy  (1) + (2) + (3) ta có hệ thức cần chứng minh là:

\(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\)

b) Từ hệ thức trên ta suy ra định lí:  “Nếu tứ diện ABCD có  \(AB \bot CD,AC \bot DB\) , nghĩa là \(\overrightarrow {AB} .\overrightarrow {CD} = 0\,\, và \,\,\overrightarrow {AC} .\overrightarrow {DB} = 0\) thì \(\overrightarrow {AD} .\overrightarrow {BC} = 0\) và do đó  \(AD \bot BC\)”

Tính tích vô hướng của hai vecto \(\overrightarrow a ,\overrightarrow b\) trong không  gian với các tọa độ đã cho là:

a) \(\overrightarrow a = (3;0; - 6),\overrightarrow b = (2; - 4;c)\)

b) \(\overrightarrow a = (1; - 5;2),\overrightarrow b = (4;3; - 5)\)

c) \(\overrightarrow a = (0;\sqrt 2 ;\sqrt 3 ),\overrightarrow b = (1;\sqrt 3 ; - \sqrt 2 )\)

Phương pháp giải

Sử dụng công thức \(\overrightarrow a .\overrightarrow b = xx' + yy' + zz'\)

Hướng dẫn giải

a) \(\overrightarrow a .\overrightarrow b =3.2-6.c= 6(1 - c)\)

b) \(\overrightarrow a .\overrightarrow b =1.4-5.3-5.2 = - 21\)

c) \(\overrightarrow a .\overrightarrow b =\sqrt 2 .\sqrt 3 -\sqrt 3 .\sqrt 2= 0\)

Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau:

a) A(4; -1; 1)  , B(2; 1; 0)

b) A(2; 3; 4)  , B(6; 0; 4)

Phương pháp giải

Sử dụng công thức tính khoảng cách \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)

Hướng dẫn giải

a) \(AB = \sqrt {{{\left( {2 - 4} \right)}^2} + {{\left( {1 + 1} \right)}^2} + {{\left( {0 - 1} \right)}^2}} = \sqrt {{2^2} + {2^2} + {1^2}} = 3\)

b) \(AB = \sqrt {{{\left( {6 - 2} \right)}^2} + {{\left( {0 - 3} \right)}^2} + {{\left( {4 - 4} \right)}^2}} = \sqrt {{4^2} + {3^2} + {0^2}} = 5\)

Trong không gian Oxyz cho tam giác ABC có tọa độ các đỉnh là: 

A(a; 0 ; 0), B(0; b; 0) , C(0; 0; c)

Chứng minh rằng tam giác ABC có ba góc nhọn.

Phương pháp giải

Sử dụng công thức \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}}\) và nhận xét nếu \(\cos \alpha > 0\) thì \(\alpha \) nhọn.

Hướng dẫn giải

Ta có: \(\overrightarrow {AB} = ( - a;b;0)\,\, và \,\,\overrightarrow {AC} = ( - a;0;c)\)

\(\begin{array}{l} \cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\\ = \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \dfrac{{{a^2}}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} > 0\\ \Rightarrow \widehat {BAC} < {90^0}\\ \overrightarrow {BA} = \left( {a; - b;0} \right),\overrightarrow {BC} = \left( {0; - b;c} \right)\\ \cos \widehat {ABC} = \cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\\ = \dfrac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} = \dfrac{{{b^2}}}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} > 0\\ \Rightarrow \widehat {ABC} < {90^0}\\ \overrightarrow {CA} = \left( {a;0; - c} \right),\overrightarrow {CB} = \left( {0; - b; - c} \right)\\ \Rightarrow \cos \widehat {BCA} = \cos \left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right)\\ = \dfrac{{\overrightarrow {CA} .\overrightarrow {CB} }}{{\left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|}} = \dfrac{{{c^2}}}{{\left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|}} > 0\\ \Rightarrow \widehat {BCA} < {90^0} \end{array}\)

Vậy tam giác ABC có ba góc nhọn.

Trong không gian Oxyz hãy lập phương trình mặt cầu trong các trường hợp sau:

a) Có tâm I(5; -3; 7) và có bán kính r = 2.

b) Có tâm là điểm C(4; -4; 2) và đi qua gốc tọa độ;

c) Đi qua điểm M(2;-1;-3) và có tâm C(3; -2; 1)

Phương pháp giải

Mặt cầu có tâm \((I\left( {a;b;c} \right)\) và bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)

Hướng dẫn giải

a) Mặt cầu có tâm \(I\left( {5; - 3;7} \right)\) và bán kính r = 2 thì có phương trình:

(x – 5)² + (y  +3)² + (z – 7)² = 4 ;

b) Mặt cầu có tâm \(C\left( {4; - 4;2} \right)\) và đi qua \(O\left( {0;0;0} \right)\) nên có bán kính \(R = OC = \sqrt {{4^2} + {4^2} + {2^2}} = 6\)

Vậy phương trình mặt cầu (x – 4)² + (y  +4)² + (z – 2)² = 36;

c) Mặt cầu có tâm \(C\left( {3; - 2;1} \right)\) và đi qua điểm \(M\left( {2; - 1; - 3} \right)\) nên có bán kính \(R = CM = \sqrt {{1^2} + {1^2} + {4^2}} = \sqrt {18}\)

Vậy phương trình mặt cầu (x – 3)² + (y + 2)² + (z – 1)² = 18.

Trong không gian Oxyz hãy xác định tâm và bán kính các mặt cầu có phương trình sau đây:

a) x² + y² + z² – 6x + 2y – 16z – 26 = 0

b) 2x² + 2y² + 2z² + 8x – 4y – 12z – 100 = 0

Phương pháp giải

Mặt cầu \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).

Hướng dẫn giải

a) Tâm I(3; -1; 8), bán kính \(R = \sqrt {{3^2} + {1^2} + {8^2} + 26} = 10\)

b) Ta có: \(2{x^2} + 2{x^2} + 2{y^2} + 2{z^2} + 8x - 4y - 12z - 100 = 0\)

\( \Leftrightarrow {x^2} + {y^2} + {z^2} + 4x - 2y - 6z - 50 = 0\)

Mặt cầu có tâm I(-2; 1; 3), bán kính \(R = \sqrt {{2^2} + {1^2} + {3^2} + 50} = 8\)

Trong không gian Oxyz hãy viết phương trình mặt cầu đi qua bốn điểm  A(1; 0; 0), B(0; -2; 0), C(0; 0; 4) và gốc tọa độ O. Hãy xác định tâm và bán kính của mặt cầu đó.

Phương pháp giải

- Gọi dạng phương trình mặt cầu là \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\)

- Thay tọa độ các điểm A, B, C, D vào phương trình, giải hệ tìm a, b, c, d

- Từ đó suy ra phương trình mặt cầu, tâm và bán kính.

Hướng dẫn giải

Phương trình mặt cầu (S) cần tìm có dạng: \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\)

Vì  \(A \in (S)\) nên ta có:  1 – 2a + d =0 (1)

\(B \in (S)\) nên ta có: 4 + 4b + d = 0 (2)

\(C \in (S)\) nên ta có: 16 – 8c + d = 0 (3)

\(D \in (S)\) nên ta có:  d = 0 (4)

Giải hệ 4 phương trình trên ta có: \(d = 0,a = \dfrac{1}{2},b = - 1,c = 2\)

Vậy mặt cầu (S) cần tìm có phương trình là: \({x^2} + {y^2} + {z^2} - x + 2y - 4z = 0\)

Phương trình mặt cầu (S) có thể viết dưới dạng:

\({\left( {x - \dfrac{1}{2}} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} - \dfrac{1}{4} - 1 - 4 = 0\)

\(\Leftrightarrow {\left( {x - \dfrac{1}{2}} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} = \dfrac{{21}}{4}\)

Vậy mặt cầu (S) có tâm \(I\left( {\dfrac{1}{2}; - 1;2} \right)\) và có bán kính \(r = \dfrac{{\sqrt {21} }}{2}\)