Giải bài tập SBT Toán 12 Bài 2: Khối đa diện lồi và khối đa diện đều

Tính sin của góc tạo bởi hai mặt kề nhau (tức là hai mặt có một cạnh chung) của một tứ diện đều.

Phương pháp giải

Ta có góc giữa hai mặt (CAB) và (DAB) bằng \(\widehat {CMD} = 2\widehat {CMN}\)

Do đó:  \(\sin \widehat {CMN} = {{{a \over 2}} \over {{{a\sqrt 3 } \over 2}}} = {1 \over {\sqrt 3 }}\)

Hướng dẫn giải

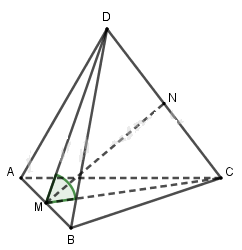
Cho tứ diện đều ABCD cạnh bằng a. Gọi M và N theo thứ tự là trung điểm của AB và CD. Khi đó góc giữa hai mặt (CAB) và (DAB) bằng \(\widehat {CMD} = 2\widehat {CMN}\)

Ta có: \(CM = {{a\sqrt 3 } \over 2},CN = {a \over 2}\)

Do đó:  \(\sin \widehat {CMN} = {{{a \over 2}} \over {{{a\sqrt 3 } \over 2}}} = {1 \over {\sqrt 3 }}\)

Từ đó suy ra: \(\sin \widehat {CMD} = {{2\sqrt 2 } \over 3}\)

Cho ba đoạn thẳng bằng nhau, đôi một vuông góc với nhau và cắt nhau tại trung điểm của chúng. Chứng minh rằng các đầu mút của ba đoạn thẳng ấy là các đỉnh của một hình bát diện đều.

Phương pháp giải

Gọi ba đoạn thẳng AC, BD, EF có độ dài bằng a cắt nhau tại trung điểm O của mỗi đường.

Khi đó OA = OB = OC  = OD = OE = OF = \(\dfrac{a}{2}\)

Tam giác EOC vuông cân tại O có OE = OC = \(\dfrac{a}{2}\) nên EC = \(\dfrac{{a\sqrt 2 }}{2}\)

Tương tự cũng tính được EA = EB = ED = FA  = FB = FC = FD = \(\dfrac{{a\sqrt 2 }}{2}\)

Vậy ABCDEF là hình bát diện đều.

Hướng dẫn giải

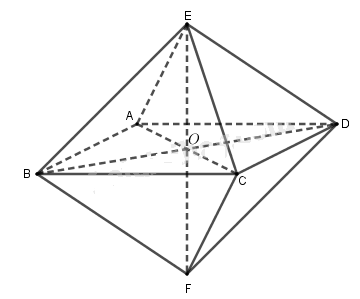
Ta chứng minh tám mặt của khối bát diện trên là các tam giác đều.

Gọi ba đoạn thẳng AC, BD, EF có độ dài bằng a cắt nhau tại trung điểm O của mỗi đường.

Khi đó OA = OB = OC  = OD = OE = OF = \(\dfrac{a}{2}\)

Tam giác EOC vuông cân tại O có OE = OC = \(\dfrac{a}{2}\) nên EC = \(\dfrac{{a\sqrt 2 }}{2}\)

Tương tự cũng tính được EA = EB = ED = FA  = FB = FC = FD = \(\dfrac{{a\sqrt 2 }}{2}\)

Vậy ABCDEF là hình bát diện đều.

Cho một khối bát diện đều. Hãy chỉ ra một mặt phẳng đối xứng, một tâm đối xứng và một trục đối xứng của nó.

Phương pháp giải

- Mặt phẳng ( P ) được gọi là mặt phẳng đối xứng của hình ( H ) nếu khi lấy đối xứng ( H ) qua ( P ) ta vẫn được chính hình ( H ).

- Một điểm O được gọi là tâm đối xứng của hình ( H ) nếu qua phép đối xứng tâm O thì hình ( H ) biến thành chính nó.

- Một đường thẳng d được gọi là trục đối xứng của hình ( H ) nếu qua phép đối trục qua đường thẳng d thì hình (H) biến thành chính nó.

Hướng dẫn giải

Ta có khối bát diện đều ABCDEF như hình vẽ. Gọi O là giao điểm của EF và (ABCD). Khi đó mặt phẳng (ABCD), điểm O và đường thẳng EF lần lượt là mặt phẳng đối xứng, tâm đối xứng và trục đối xứng của khối bát diện đều đã cho.

Cho khối bát diện đều ABCDEF (h.1.9). Gọi O là giao điểm của AC và BD, M và N theo thứ tự là trung điểm của AB và AE. Tính diện tích thiết diện tạo bởi khối bát diện đó và mặt phẳng (OMN).

Phương pháp giải

Dựng thiết diện của bát hiện đều khi cắt bởi (OMN)

Do \(\left( {ADE} \right)//\left( {BCF} \right)\) nên \(\left( {OMN} \right)\) cắt \(\left( {BCF} \right)\) theo giao tuyến qua S và song song với NP cắt FC tại trung điểm R.

Tương tự, \(\left( {OMN} \right)\) cắt DC tại trung điểm Q của DC.

Do đó diện tích thiết diện là: \(S = 6{S_{\Delta OMN}} \)

Hướng dẫn giải

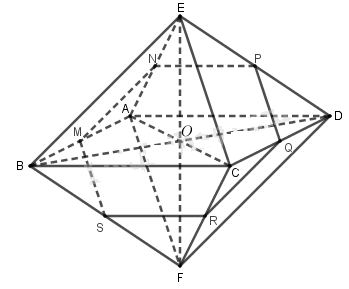
Ta có khối bát diện đều ABCDEF, cạnh a. Do \(MN//\left( {DEBF} \right) \)nên giao của mặt phẳng \(\left( {OMN} \right)\) với mặt phẳng \(\left( {DEBF} \right)\) là đường thẳng qua O và song song với MN.

Trong \(\left( {DEBF} \right)\), qua O kẻ đường thẳng \(PS//MN\left( {P \in DE,S \in BF} \right)\)

Do \(\left( {ADE} \right)//\left( {BCF} \right)\) nên \(\left( {OMN} \right)\) cắt \(\left( {BCF} \right)\) theo giao tuyến qua S và song song với NP cắt FC tại trung điểm R.

Tương tự, \(\left( {OMN} \right)\) cắt DC tại trung điểm Q của DC.

Suy ra thiết diện tạo bởi hình bát diện đã cho với mặt phẳng \(\left( {OMN} \right)\) là lục giác đều có cạnh bằng \(\dfrac{a}{2}\)

Do đó diện tích thiết diện là: \(S = 6{S_{\Delta OMN}} = 6.{\left( {\dfrac{a}{2}} \right)^2}.\dfrac{{\sqrt 3 }}{4} = \dfrac{{3\sqrt 3 }}{8}{a^2}\)