Giải bài tập SBT Toán 12 Bài 1: Khái niệm về khối đa diện

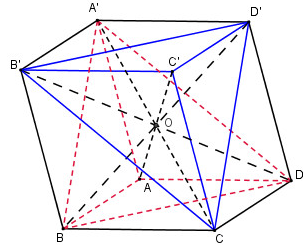
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai tứ diện A’ABD và CC’D’B’ bằng nhau.

Phương pháp giải

Dùng phép đối xứng qua tâm của hình hộp.

Hướng dẫn giải

Xét 2 tứ diện A'ABD và CC'D'B'

Dùng phép đối xứng qua tâm O của hình hộp

Ta có:

A' đối xứng C qua O

A đối xứng C' qua O

B đối xứng D' qua O

D đối xứng B' qua O

Suy ra tứ diện A'ABD bằng tứ diện CC'D'B'.

Cho lăng trụ ABC.A’B’C’. Gọi E, F, G lần lượt là trung điểm của AA’, BB’, CC’. Chứng minh rằng các lăng trụ ABC.EFG và EFG.A’B’C’ bằng nhau

Phương pháp giải

Dùng phép tịnh tiến vecto \(\overrightarrow{AE}\) biến lăng trụ ABC.EFG thành lăng trụ EFG.A’B’C.

Hướng dẫn giải

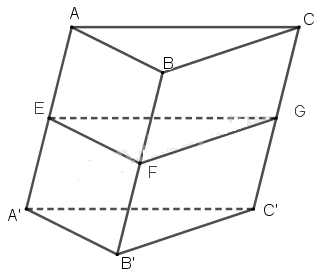
Vì E, F, G lần lượt là trung điểm của AA’, BB’, CC’ nên ta có:

Ta có: \(T_{\overrightarrow{AE}}(A)=E; T_{\overrightarrow{AE}}(B)=F; T_{\overrightarrow{AE}}(C)=G\)

\(T_{\overrightarrow{AE}}(E)=A’; T_{\overrightarrow{AE}}(F)=B’; T_{\overrightarrow{AE}}(G)=C’\)

\(\Rightarrow T_{\overrightarrow{AE}}(ABC.EFG)=EFG.A’B’C’\)

Vậy lăng trụ ABC.EFG và EFG.A’B’C’ bằng nhau.

Chia hình chóp tứ giác đều thành tám hình chóp bằng nhau.

Phương pháp giải

Chia đáy hình chóp thành 8 tam giác bằng nhau rồi chứng minh các hình chóp có đỉnh là đỉnh của hình chóp ban đầu và đáy là mỗi tam giác vừa có được thì bằng nhau.

Sử dụng lý thuyết: Hai tứ diện có các cạnh tương ứng bằng nhau thì bằng nhau

Hướng dẫn giải

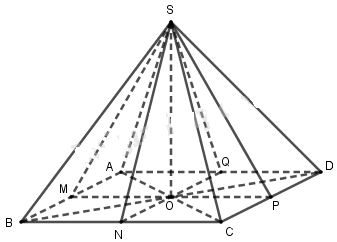
Gọi \(O = AC \cap BD\), các điểm M, N, P, Q lần lượt là trung điểm của mỗi đoạn thẳng AB, BC, CD, DA.

Khi đó các tam giác AOM, BOM, BON, CON, COP, DOP, DOQ, AOQ bằng nhau.

Ta chứng minh các hình chóp S.AOM, S.BOM, S.BON, S.CON, S.COP, S.DOP, S.DOQ, S.AOQ bằng nhau.

Xét hai hình chóp S.AOM và S.BOM có SA = SB,AO = BO,AM = BM, SO chung và SM chung, OM chung.

Do đó hai tứ diện có các cạnh tương ứng bằng nhau thì bằng nhau.

Tương tự ta có 8 hình chóp bằng nhau.

Chia một khối tứ diện đều thành bốn tứ diện bằng nhau.

Phương pháp giải

- Gọi G là trọng tâm tứ diện đều ABCD.

- Chứng minh các hình tứ diện có đỉnh là G và đáy và các mặt bên của tứ diện đã cho bằng nhau.

Hướng dẫn giải

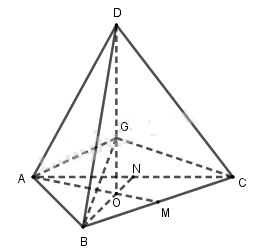
Xét tứ diện đều ABCD. Gọi G là giao điểm của các đường thẳng nối đỉnh với trọng tâm của mặt đối diện.

Khi đó dễ thấy các tứ diện GABC, GBCD, GCDA, GDAB bằng nhau.

Thật vậy, các tứ diện trên đều có đáy là các tam giác đều có cạnh bằng nhau, các cạnh bên GA = GB = GC = GD.

Vậy ta đã chia được tứ diện đều thành 4 tứ diện bằng nhau.

Chứng minh rằng mỗi hình đa diện có ít nhất 4 đỉnh.

Phương pháp giải

Sử dụng định nghĩa hình đa diện:

Hình (H)  gồm các hữu hạn các đa giác thỏa mãn hai điều kiện:

+ Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.

+ Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.

Hướng dẫn giải

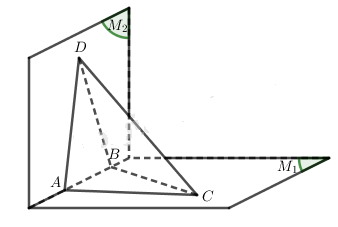
Gọi \({M_1}\) là một mặt của hình đa diện ( H ) chứa ba đỉnh A, B, C.

Khi đó AB, BC là hai cạnh của ( H ).

Gọi \({M_2}\) là mặt khác với \({M_1}\) và có chung cạnh AB với \({M_1}\)

Khi đó \({M_2}\) còn có ít nhất một đỉnh D khác với A và B.

Nếu \(D \equiv C\) thì \({M_1}\) và \({M_2}\) có hai cạnh chung AB và BC (vô lý).

Vậy D phải khác C. Do đó \(\left( H \right)\) có ít nhất bốn đỉnh A, B, C, D.