Giải bài tập SBT Hình học 11 Ôn tập chương 1: Phép dời hình và phép đồng dạng

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x - 5y + 3 = 0 và vectơ \(\overrightarrow v = \left( {2;3} \right)\).Hãy viết phương trình đường thẳng d' là ảnh của d qua phép tịnh tiến theo vectơ \(\overrightarrow v\).

Phương pháp giải:

- Gọi phương trình d'.

- Lấy một điểm \(A \in d \), tìm ảnh A' của A qua \({T_{\overrightarrow v }}\).

- Cho \(A' \in d'\) và suy ra phương trình của d'.

Hướng dẫn giải:

Gọi d': 3x - 5y + c = 0.

Lấy \(A\left( {4;3} \right) \in d \), gọi \(A'\left( {x;y} \right) = {T_{\overrightarrow v }}\left( A \right)\).

Khi đó \(\left\{ \begin{array}{l}x = 4 + 2 = 6\\y = 3 + 3 = 6\end{array} \right.\) nên \(A'\left( {6;6} \right).\)

Mà \(A' \in d'\) nên \(3.6 - 5.6 + c = 0 \Leftrightarrow c = 12.\)

Vậy phương trình d': \(3{\rm{x}} - 5y + 12 = 0.\)

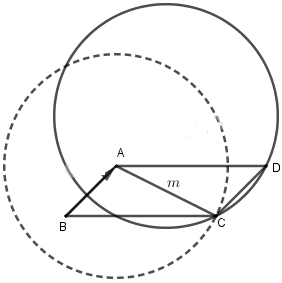
Cho hình bình hành ABCD có AB cố định, đường chéo AC có độ dài bằng m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm D thuộc một đường tròn cố định.

Phương pháp giải:

Tìm quỹ tích điểm C và sử dụng tính chất của phép tịnh tiến để suy ra quỹ tích điểm D.

Hướng dẫn giải:

Dễ thấy \(\overrightarrow {CD} = \overrightarrow {AB}\) và A, B cố định nên \(D = {T_{\overrightarrow {BA} }}\left( C \right).\)

Do C chạy trên đường tròn \(\left( C \right)\) tâm A bán kính m, trừ ra giao điểm của \(\left( C \right)\) với đường thẳng AB.

Nên D thuộc đường tròn là ảnh của đường tròn nói trên qua phép tịnh tiến theo vectơ \(\overrightarrow {BA}\).

Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.

Phương pháp giải:

- Giả sử dựng được hai điểm M,N thỏa mãn bài toán.

- Sử dụng các tính chất hình học đã biết để suy ra cách dựng.

Hướng dẫn giải:

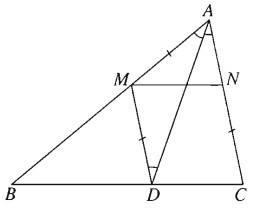
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài.

Qua M kẻ đường thẳng song song với AC cắt BC tại D.

Khi đó tứ giác MNCD là hình bình hành \( \Rightarrow CN = DM.\)

Mà CN = AM (giả thiết) \( \Rightarrow AM = DM\) hay \(\Delta ADM\) cân tại M.

Do đó \(\widehat {MAD} = \widehat {MDA} \), mà \(\widehat {MDA} = \widehat {DAC}\) (so le trong) nên \(\widehat {MAD} = \widehat {DAC}\).

Suy ra AD là phân giác trong của góc A nên ta dựng được AD.

Ta lại có \(\overrightarrow {NM} = \overrightarrow {CD} \) nên \(M = {T_{\overrightarrow {CD} }}\left( N \right)\)

Từ đó suy ra cách dựng:

- Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.

- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ \(\overrightarrow {CD}\). d cắt AB tại M.

- Dựng N sao cho \(\overrightarrow {NM} = \overrightarrow {C{\rm{D}}}\).

Khi đó dễ thấy M,N thỏa mãn điều kiện đầu bài.

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x - 2y - 6 = 0

a) Viết phương trình của đường thẳng \({d_1}\) là ảnh của d qua phép đối xứng qua trục Oy;

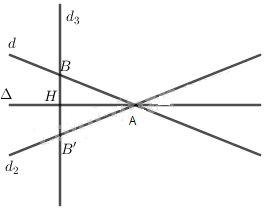
b) Viết phương trình của đường thẳng \({d_2}\) là ảnh của d qua phép đối xứng qua đường thẳng \(\Delta \) có phương trình x + y - 2 = 0. 

Phương pháp giải:

a) Sử dụng biểu thức tọa độ của phép đối xứng trục Oy: \(\left\{ \begin{array}{l}x' = - x\\y' = y\end{array} \right.\)

b) - Tìm giao điểm A của d và \(\Delta\).

- Lấy một điểm \(B \in d \), tìm ảnh B' của B qua \({D_\Delta }\).

- Viết phương trình AB' và kết luận.

Hướng dẫn giải:

a) Với mỗi điểm \(M\left( {x;y} \right)\) bất kì thuộc d, gọi \(M'\left( {x';y'} \right) = {D_{Oy}}\left( M \right)\)

Khi đó \(\left\{ \begin{array}{l}x' = - x\\y' = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - x'\\y = y'\end{array} \right.\)

Mà \(M\left( {x;y} \right) \in d:3x - 2y - 6 = 0\) nên \(3.\left( { - x'} \right) - 2.y' - 6 = 0\) hay 3x' + 2y' + 6 = 0.

Vậy \({d_1}:3x + 2y + 6 = 0\).

b)

Dễ thấy \(\Delta \) và d cắt nhau do \(\dfrac{3}{1} \ne \dfrac{{ - 2}}{1}\) nên gọi \(A\left( {x;y} \right) = d \cap \Delta\).

Tọa độ của A thỏa mãn hệ phương trình

\(\left\{ \begin{array}{l}3x - 2y - 6 = 0\\x + y - 2 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x - 2y = 6\\x + y = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right. \\ \Rightarrow A\left( {2;0} \right).\)

Lấy \(B\left( {0; - 3} \right) \in d \), gọi \(B'\left( {x;y} \right) = {D_\Delta }\left( B \right) \), ta tìm tọa độ B'.

Gọi \({d_3}\) là đường thẳng qua \(B\left( {0; - 3} \right)\) và vuông góc \(\Delta\). Khi đó \(\overrightarrow {{n_{{d_3}}}} \bot \overrightarrow {{n_d}} \Rightarrow \overrightarrow {{n_{{d_3}}}} = \left( {1; - 1} \right).\)

Phương trình \({d_3}:1\left( {x - 0} \right) - 1\left( {y + 3} \right) = 0\) hay \(x - y - 3 = 0.\)

Gọi \(H = \Delta \cap {d_3}\) thì tọa độ của H thỏa mãn hệ phương trình

\(\left\{ \begin{array}{l}x + y - 2 = 0\\x - y - 3 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{5}{2}\\y = - \dfrac{1}{2}\end{array} \right. \\ \Rightarrow H\left( {\dfrac{5}{2}; - \dfrac{1}{2}} \right).\)

Mà \(B' = {D_\Delta }\left( B \right)\) nên H là trung điểm của BB'

\( \Rightarrow \left\{ \begin{array}{l}{x_{B'}} = 2{x_H} - {x_B}\\{y_{B'}} = 2{y_H} - {y_B}\end{array} \right.\)

Hay

\( \left\{ \begin{array}{l}{x_{B'}} = 2.\dfrac{5}{2} - 0 = 5\\{y_{B'}} = 2.\left( { - \dfrac{1}{2}} \right) - \left( { - 3} \right) = 2\end{array} \right. \\ \Rightarrow B'\left( {5;2} \right).\)

Đường thẳng \({d_2}\) đi qua hai điểm \(A\left( {2;0} \right)\) và \(B'\left( {5;2} \right)\) nên có phương trình \(\dfrac{{x - 2}}{{5 - 2}} = \dfrac{{y - 0}}{{2 - 0}}\)  hay 2x - 3y - 4 = 0.

Vậy \({d_2}:2x - 3y - 4 = 0.\)

Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A, B ), ta xét điểm N sao cho AMBN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.

Phương pháp giải:

Dựng hình và nhận xét

Hướng dẫn giải:

Gọi \( E = AB \cap MN\) thì E là trung điểm của AB, MN.

Dễ thấy \(N = {D_E}\left( M \right)\) và \(M \in \left( C \right)\) nên tập hợp các điểm N thuộc đường tròn \(\left( {C'} \right)\) là ảnh của (C) qua phép đối xứng qua trung điểm của AB.

Cho hai đường tròn có cùng tâm O, bán kính lần lượt là R và r, \(\left( {R > r} \right)\). A là một điểm thuộc đường tròn bán kính r. Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C, D sao cho CD = 3AB

Phương pháp giải:

- Giả sử dụng được hai điểm C, D thỏa mãn bài toán.

- Sử dụng kiến thức hình học đã biết để suy ra cách dựng.

Hướng dẫn giải:

Gọi (C) là đường tròn tâm O bán kính r, \(\left( {{C_1}} \right)\) là đường tròn tâm O bán kính R.

Giả sử đường thẳng đã dựng được. Khi đó DA = AB = BC nên \(D = {D_A}\left( B \right)\).

Mà \(B \in \left( C \right)\) nên \(D \in \left( {C'} \right)\) là ảnh của (C) qua phép đối xứng qua tâm A.

Lại có \(D \in \left( C \right)\) (giả thiết) nên \(D = \left( {C'} \right) \cap \left( {{C_1}} \right).\)

Từ đó ta có cách dựng:

+) Dựng ảnh (C') của (C) qua phép đối xứng tâm A.

+) Nếu (C') không cắt (C) thì không có điểm C, D thỏa mãn bài toán.

+) Nếu (C') tiếp xúc \(\left( {{C_1}} \right)\) tại duy nhất một điểm thì có một cặp điểm C, D thỏa mãn bài toán.

+) Nếu (C') cắt \(\left( {{C_1}} \right)\) tại hai điểm phân biệt thì có hai cặp điểm C, D thỏa mãn bài toán.

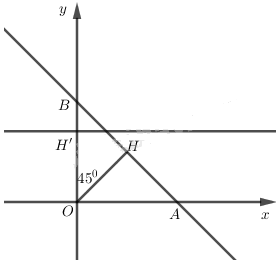
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Hãy viết phương trình của đường thẳng d' là ảnh của d qua phép quay tâm O góc \(45^\circ\).

Phương pháp giải:

- Lấy điểm \(H\left( {1;1} \right)\) thuộc d.

- Tìm ảnh \(H' = {Q_{\left( {O,{{45}^0}} \right)}}\left( H \right)\).

- Viết phương trình đường thẳng đi qua H' và vuông góc OH' rồi kết luận.

Hướng dẫn giải:

Lấy \(H\left( {1;1} \right) \in d\) và \(OH \bot d \Rightarrow \) góc giữa OH và trục Oy bằng \({45^0}\).

Gọi \(H' = {Q_{\left( {O,{{45}^0}} \right)}}\left( H \right)\) thì \(H' \in Oy\) và \(OH' = OH = \sqrt 2 \) nên \(H' = \left( {0;\sqrt 2 } \right)\).

Từ đó suy ra d' phải qua H' và vuông góc với OH'.

Vậy phương trình của d' là \(y = \sqrt 2\).

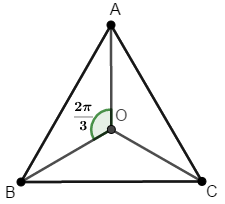
Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng \(60^\circ\). Chứng minh rằng tứ giác MPNQ là một hình thang cân.

Phương pháp giải:

Xét phép quay tâm G góc quay \({120^0}\) và nhận xét.

Hướng dẫn giải:

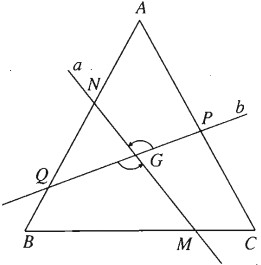
Gọi \({Q_{\left( {G;{{120}^0}} \right)}}\) là phép quay tâm G góc \({120^0}\).

Phép quay này biến b thành a, biến CA thành AB.

Mà \(P = b \cap CA,N = a \cap AB\) nên \({Q_{\left( {G,{{120}^0}} \right)}}\left( P \right) = N.\)

Tương tự \({Q_{\left( {G;{{120}^0}} \right)}}\left( Q \right) = M \) suy ra GP = GN,GQ = GM.

\( \Rightarrow \Delta GNQ = \Delta GPM \Rightarrow NQ = PM\)

Vì \({Q_{\left( {G;{{120}^0}} \right)}}\) biến PQ thành NM nên PQ = NM.

Từ đó suy ra hai tam giác NQM và PMQ bằng nhau. Do đó \(\widehat {NQM} = \widehat {PMQ}.\)

Tương tự \(\widehat {QNP} = \widehat {MPN}.\)

Từ đó suy ra \(\widehat {PNQ} + \widehat {NQM} = {180^0}\)

Do đó \(NP\parallel QM\).

Vậy ta có tứ giác MPNQ là hình thang cân.

Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng:

\(\overrightarrow {A'B'}.\overrightarrow {A'C'} = {k^2}\overrightarrow {AB.} \overrightarrow {AC}.\)

Phương pháp giải:

Sử dụng định nghĩa phép đồng dạng tỉ số k biến M thành M' và N thành N' thì M'N' = kMN.

Hướng dẫn giải:

Theo định nghĩa của phép đồng dạng ta có B'C' = kBC, từ đó suy ra \(B'C{'^2} = {k^2}B{C^2}. \)

\( \Rightarrow {\left( {\overrightarrow {A'C'} - \overrightarrow {A'B'} } \right)^2} = {k^2}{\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)^2} \\ \Rightarrow A'C{'^2} - 2\overrightarrow {A'C'}.\overrightarrow {A'B'} + A'B{'^2} = {k^2}\left( {A{C^2} - 2\overrightarrow {AC}.\overrightarrow {AB} + A{B^2}} \right)\)

Mà \(A'C{'^2} = {k^2}A{C^2},A'B{'^2} = {k^2}A{B^2}\) 

Nên \(\overrightarrow {A'C'}.\overrightarrow {A'B'} = {k^2}\overrightarrow {AC}.\overrightarrow {AB} \) (đpcm).

Gọi A', B' và C' tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu \(\overrightarrow {AB} = p\overrightarrow {AC} \) thì \(\overrightarrow {A'B'} = p\overrightarrow {A'C'} \), trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A' và C'.

Phương pháp giải:

Sử dụng định nghĩa phép đồng dạng tỉ số k biến M thành M' và N thành N' thì M'N' = kMN.

Hướng dẫn giải:

Xét phép đồng dạng tỉ số k biến các điểm A, B, C thành A', B', C'.

Khi đó theo bài 1.39 ta có:

 \(A'C{'^2} = {k^2}A{C^2},A'B{'^2} = {k^2}A{B^2}, \overrightarrow {A'C'}.\overrightarrow {A'B'} = {k^2}\overrightarrow {AC}.\overrightarrow {AB}.\)

Ta có:

\({\left( {\overrightarrow {A'B'} - p\overrightarrow {A'C'} } \right)^2} \\ = A'B{'^2} - 2p\overrightarrow {A'B'}.\overrightarrow {A'C'} + {p^2}A'C{'^2} \\= {k^2}\left( {A{B^2} - 2p\overrightarrow {AB}.\overrightarrow {AC} + {p^2}A{C^2}} \right) \\= {k^2}{\left( {\overrightarrow {AB} - p\overrightarrow {AC} } \right)^2} = 0\)

Từ đó suy ra \(\overrightarrow {A'B'} - p\overrightarrow {A'C'} = \overrightarrow 0\)

Giả sử ba điểm A,B,C thẳng hàng và điểm B nằm giữa hai điểm A và C.

Khi đó \(\overrightarrow {AB} = p\overrightarrow {AC} \), với 0 < p < 1.

Khi đó \(\overrightarrow {A'B'} = p\overrightarrow {A'C'} \), với 0 < p < 1.

Do đó ba điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.

Trong mặt phẳng Oxy xét phép biến hình F biến mỗi điểm \( M\left( {x;y} \right)\) thành \(M'\left( {2{\rm{x}} - 1; - 2y + 3} \right)\). Chứng minh F là một phép đồng dạng.

Phương pháp giải:

Sử dụng định nghĩa phép đồng dạng tỉ số k biến M thành M' và N thành N' thì M'N' = kMN. 

Hướng dẫn giải:

Lấy điểm \(N\left( {{x_1};{y_1}} \right) \), thì điểm \(N'\left( {2{x_1} - 1; - 2{y_1} + 3} \right) = F\left( N \right).\)

Ta có:

\(M'N{'^2} \\= {\left( {2{{\rm{x}}_1} - 2{\rm{x}}} \right)^2} + {\left( { - 2{y_1} + 2y} \right)^2} \\= 4\left[ {{{\left( {{x_1} - x} \right)}^2} + {{\left( {{y_1} - y} \right)}^2}} \right] \\= 4M{N^2}\)

Từ đó suy ra với hai điểm M, N tùy ý và M', N' lần lượt là ảnh của chúng qua F ta có M'N' = 2MN.

Vậy F là phép đồng dạng với tỉ số đồng dạng là 2.

Dựng tam giác BAC vuông cân tại A có C là một điểm cho trước, còn hai đỉnh A,B lần lượt thuộc hai đường thẳng a,b song song với nhau cho trước.

Phương pháp giải:

- Giả sử dựng được hình vẽ.

- Sử dụng tính chất hình học đã biết suy ra cách dựng.

Hướng dẫn giải:

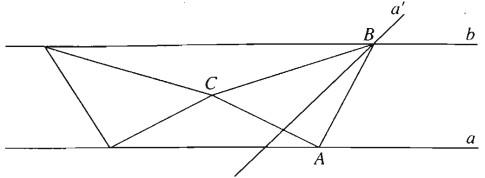
Ta có: \(\Delta BAC\) vuông cân tại A nên \(\widehat {ACB} = {45^0}\).

Xem B là ảnh của A qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm C góc \( \pm {45^0} \) và phép vị tự tâm C tỉ số \(k = \sqrt 2\).

Vì A thuộc a nên B thuộc đường thẳng a' là ảnh của a qua phép đồng dạng nói trên.

Vậy B là giao của a' và b.

Từ đó suy ra cách dựng:

- Dựng đường thẳng a'' là ảnh của a qua phép quay tâm C góc quay \( \pm {45^0}\).

- Dựng đường thẳng a' là ảnh của a'' qua phép vị tự tâm C tỉ số \(\sqrt 2.\)

- Lấy \(B = a' \cap b.\)

- Dựng đường trung trực của BC , đường này cắt a tại A.

Bài toán có hai nghiệm hình.

Trong mặt phẳng Oxy cho đường thẳng d: 2x - y + 6 = 0. Viết phương trình đường thẳng d' là ảnh của d qua phép đối xứng tâm \(I\left( { - 2;1} \right).\)

Phương pháp giải:

Sử dụng biểu thức tọa độ của phép đối xứng tâm \(\left\{ \begin{array}{l}x' = 2{x_I} - x\\y' = 2{y_I} - y\end{array} \right.\)

Hướng dẫn giải:

Gọi M(x; y) bất kì thuộc d, M'(x'; y') là ảnh của M(x; y) qua \({D_I}.\)

Dùng công thức tọa độ của phép đối xứng tâm \(I\left( { - 2;1} \right)\), ta có:

\( M' = {D_1}\left( M \right) \\ \Rightarrow \left\{ \begin{array}{l}x' = 2.\left( { - 2} \right) - x\\y' = 2.1 - y\end{array} \right. \\ \Rightarrow \left\{ \begin{array}{l}x = - 4 - x'\\y = 2 - y'\end{array} \right.\)

Thế \(\left( {x;y} \right)\) vào phương trình d, ta có phương trình

\(d':2\left( { - 4 - x'} \right) - \left( {2 - y'} \right) + 6 = 0 \Rightarrow d':2{\rm{x}}' - y' + 4 = 0.\)

Đổi kí hiệu, ta có phương trình \(d':2{\rm{x}} - y + 4 = 0.\)

Trong mặt phẳng Oxy cho đường tròn \(\left( C \right):{x^2} + {y^2} + 2x - 4y - 11 = 0\). Tìm phép tịnh tiến biến (C) thành \( \left( {C'} \right):{\left( {x - 10} \right)^2} + {\left( {y + 5} \right)^2} = 16\).

Phương pháp giải:

- Tìm tâm và bán kính của đường tròn (C).

- Sử dụng tính chất của phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính và \(\overrightarrow {II'} = \overrightarrow v.\)

Hướng dẫn giải:

(C) có tâm \(I\left( { - 1;2} \right)\), bán kính R = 4.

 (C') có tâm \(I'\left( {10; - 5} \right)\), bán kính R' = 4.

Vậy \(\left( {C'} \right) = {T_{\vec v}}\left( C \right) \Rightarrow \overrightarrow v = \overrightarrow {II'} = \left( {11; - 7} \right).\)

Trong mặt phẳng Oxy cho hai đường thẳng d: x - 5y + 7 = 0 và d': 5x - y - 13 = 0. Tìm phép đối xứng qua trục biến d thành d'.

Phương pháp giải:

Phép đối xứng trục biến d thành d' mà d và d' không song song thì trục đối xứng là đường phân giác của góc tạo bởi d và d'.

Hướng dẫn giải:

Nhận xét d và d' không song song nên phép đối xứng trục biến d thành d' có trục là phân giác của góc tạo bởi d và d'.

Phương trình các đường phân giác là:

\( \dfrac{{\left| {x - 5y + 7} \right|}}{{\sqrt {26} }} = \dfrac{{\left| {5{\rm{x}} - y - 13} \right|}}{{\sqrt {26} }} \\ \Leftrightarrow \left[ \begin{array}{l}x + y - 5 = 0\\x - y - 1 = 0\end{array} \right.\)

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x - y - 3 = 0. Viết phương trình đường thẳng \({d_1}\) là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm \(I\left( { - 1;2} \right)\) và phép quay tâm O góc quay \( - 90^\circ.\)

Phương pháp giải:

- Sử dụng biểu thức tọa độ của phép đối xứng tâm I là \(\left\{ \begin{array}{l}x' = 2{x_I} - x\\y' = 2{y_I} - y\end{array} \right.\)

- Sử dụng biểu thức tọa độ của phép quay tâm O góc quay \( - {90^0}\) biến điểm M(x; y) thành M'(x', y') là \(\left\{ \begin{array}{l}x' = y\\y' = - x\end{array} \right.\)

Hướng dẫn giải:

Giả sử \({M_1} = {D_I}\left( M \right)\) và \(M' = {Q_{\left( {O; - {{90}^0}} \right)}}\left( {{M_1}} \right).\)

Ta có:

\( \left\{ \begin{array}{l}{x_1} = - 2 - x\\{y_1} = 4 - y\end{array} \right.\) và \( \left\{ \begin{array}{l}x' = {y_1}\\y' = - {x_1}\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}x' = 4 - y\\y' = 2 + x\end{array} \right. \\ \Rightarrow \left\{ \begin{array}{l}4 - x'\\x = - 2 + y'\end{array} \right.\)

Thế (x; y) theo (x'; y') vào phương trình d ta có:

\(3\left( {y' - 2} \right) - \left( {4 - x'} \right) - 3 = 0 \Leftrightarrow x' + 3y' - 13 = 0.\)

Vậy phương trình d' là x + 3y - 13 = 0.

Trong mặt phẳng Oxy cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\). Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép đối xứng trục d: x = 1.

Phương pháp giải:

Tìm ảnh của tâm đường tròn qua trục d. 

Hướng dẫn giải:

Đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\) có tâm I(1; 2) và bán kính R = 3.

Gọi I' là ảnh của I qua phép đối xứng trục qua đường thẳng d: x = 1.

Dễ thấy \(I\left( {1;2} \right) \in d\) nên \(I' \equiv I \) hay đường tròn \(\left( {C'} \right) \equiv \left( C \right).\)

Vậy \(\left( {C'} \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9.\)

Trong mặt phẳng Oxy cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\). Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép quay \({Q_{\left( {0; - {{90}^0}} \right)}}\) với O là gốc tọa độ.

Phương pháp giải:

- Tìm tâm và bán kính của đường tròn đã cho.

- Tìm ảnh của tâm qua phép quay \({Q_{\left( {0; - {{90}^0}} \right)}}.\)

- Viết phương trình đường tròn mới và kết luận.

Hướng dẫn giải:

(C) có tâm I(1; 2), bán kính R = 3.

Gọi I', R' lần lượt là tâm và bán kính của đường tròn ảnh, ta có:

\( I' = {Q_{\left( {O, - {{90}^0}} \right)}}\left( I \right) \Leftrightarrow \left\{ \begin{array}{l}x' = y = 2\\y' = - x = - 1\end{array} \right.\) và R' = 3.

Vậy phương trình (C') là \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 9.\)

Trong mặt phẳng (Oxy) cho điểm A(2; 5). Phép tịnh tiến theo véctơ \(\overrightarrow v \left( {1;2} \right)\) biến A thành điểm có tọa độ

A. (3; 1)         B. (1; 6)

C. (3; 7)         D. (4; 7) 

Phương pháp giải:

Sử dụng công thức tọa độ của phép tịnh tiến: \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\).

Hướng dẫn giải:

Ta có:

\(A' = {T_{\overrightarrow v }}\left( A \right) \\ \Leftrightarrow \left\{ \begin{array}{l}x' = 2 + 1 = 3\\y' = 5 + 2 = 7\end{array} \right.\\ \Rightarrow A'\left( {3;7} \right).\)

Vậy chọn C.

Trong mặt phẳng Oxy cho điểm A(4; 5). Qua phép tịnh tiến theo véctơ \(\overrightarrow v \left( {2;1} \right)\), A là ảnh của điểm có tọa độ

A. (3; 1)         B. (1; 6)

C. (4; 7)         D. (2; 4)

Phương pháp giải:

Sử dụng công thức tọa độ của phép tịnh tiến: \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\).

Hướng dẫn giải:

Gọi A'(x'; y') là điểm thỏa mãn \(A = {T_{\overrightarrow v }}\left( {A'} \right).\)

Khi đó

\(\overrightarrow {A'A} = \overrightarrow v \\ \Leftrightarrow \left\{ \begin{array}{l}4 - x' = 2\\5 - y' = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x' = 2\\y' = 4\end{array} \right.\)

Vậy chọn D.

Có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó?

A. Không có            B. Chỉ có một

C. Chỉ có hai           D. Vô số

Phương pháp giải:

Sử dụng tính chất của phép tịnh tiến, biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

Hướng dẫn giải:

Phép tịnh tiến theo véc tơ có giá song song hoặc trùng với đường thẳng thì biến đường thẳng thành chính nó.

Có vô số véc tơ như vậy nên có vô số phép tịnh tiến.

Vậy chọn D.

Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?

A. Không có           B. Chỉ có một

C. Chỉ có hai          D. Vô số

Phương pháp giải:

Sử dụng tính chất của phép tịnh tiến, biến đường tròn thành đường tròn có cùng bán kính.

Hướng dẫn giải:

Phép tịnh tiến biến đường tròn cho trước thành chính nó nếu nó biến tâm đường tròn thành chính tâm ấy.

Đây là phép tịnh tiến theo véctơ \(\overrightarrow 0 \) hay phép đồng nhất.

Do đó chỉ có một phép tịnh tiến duy nhất.

Vậy chọn B.

Có bao nhiêu phép tịnh tiến biến một hình vuông thành chính nó?

A. Không có           B. Chỉ có một

C. Chỉ có bốn          D. Vô số

Phương pháp giải:

Sử dụng tính chất của phép tịnh tiến để nhận xét.

Hướng dẫn giải:

Phép tịnh tiến biến hình vuông thành chính nó nếu đó là phép tịnh tiến theo vectơ \(\overrightarrow 0 \) hay phép đồng nhất.

Do đó chỉ có một phép tịnh tiến duy nhất.

Vậy chọn B.

Trong mặt phẳng (Oxy) cho điểm M(2; 3), ảnh của M qua phép đối xứng trục Ox có tọa độ

A. (3; 2)         B. (2; -3)

C. (3; -2)       D. (-2; 3)

Phương pháp giải:

Sử dụng biểu thức tọa độ của phép đối xứng trục Ox: \(\left\{ \begin{array}{l}x' = x\\y' = - y\end{array} \right..\)

Hướng dẫn giải:

Ta có:

\( M\left( {2;3} \right) \\ \Rightarrow M' = {D_{Ox}}\left( M \right) \\ \Leftrightarrow \left\{ \begin{array}{l}x' = 2\\y' = - 3\end{array} \right.\)

Vậy chọn B.

Trong mặt phẳng (Oxy) cho điểm M(2; 3), qua phép đối xứng trục Oy thì M là ảnh của điểm có tọa độ

A. (3; 2)         B. (2; -3)

C. (3; -2)       D. (-2; 3)

Phương pháp giải:

Sử dụng biểu thức tọa độ của phép đối xứng trục Oy: \(\left\{ \begin{array}{l}x' = - x\\y' = y\end{array} \right..\)

Hướng dẫn giải:

Gọi M' là điểm thỏa mãn \(M = {D_{Oy}}\left( {M'} \right)\), khi đó \(M' = {D_{Oy}}\left( M \right).\)

Suy ra \(\left\{ \begin{array}{l}x' = - x = - 2\\y' = y = 3\end{array} \right.\)  hay M'(-2; 3)

Vậy chọn D.

Trong mặt phẳng (Oxy) cho điểm M(2; 3), ảnh của M qua phép đối xứng trục là đường thẳng x - y = 0 có tọa độ

A. (3; 2)         B. (2; -3)

C. (3; -2)       D. (-2; 3)

Phương pháp giải:

Sử dụng công thức tọa độ của phép đối xứng trục qua đường phân giác trong của góc phần tư thứ nhất y = x là \(\left\{ \begin{array}{l}x' = y\\y' = x\end{array} \right.\).

Hướng dẫn giải:

Gọi \(M' = {D_\Delta }\left( M \right)\) với \(\Delta :x - y = 0\) là đường phân giác trong của góc phần tư thứ nhất.

Khi đó \(\left\{ \begin{array}{l}x' = y = 3\\y' = x = 2\end{array} \right.\) hay \(M'\left( {3;2} \right).\)

Vậy chọn A.

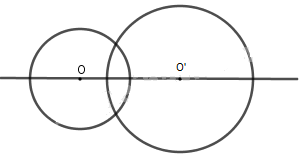
Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?

A. Không có           B. Chỉ có một

C. Chỉ có hai           D. Vô số

Phương pháp giải:

Dựng hình và đếm trục đối xứng, dựa vào định nghĩa trục đối xứng của một hình. 

Hướng dẫn giải:

Trục đối xứng của hình trên là đường thẳng đi qua tâm của hai đường tròn.

Vậy chọn B.

Khẳng định nào sau đây là đúng?

A. Đường tròn là hình có vô số trục đối xứng

B. Một hình có vô số trục đối xứng thì hình đó phải là đường tròn.

C. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm những đường tròn đồng tâm.

D. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm hai đường thẳng vuông góc.

Phương pháp giải:

Nhận xét tính đúng sai của các đáp án, chú ý chỉ ra phản ví dụ.

Hướng dẫn giải:

Đáp án A: Đúng vì trục đối xứng của đường tròn là đường kính, mà đường tròn có vô số đường kính nên có vô số trục đối xứng.

Đáp án B, C sai vì một hình có vô số trục đối xứng ngoài đường tròn, hai đường tròn đồng tâm ra thì còn có đường thẳng và nhiều hình khác.

Đáp án D sai vì hai đường thẳng vuông góc chỉ có 4 trục đối xứng chứ không phải có vô số trục đối xứng.

Vậy chọn A.

Trong mặt phẳng Oxy, cho hai điểm I(1; 2) và M(3; -1). Ảnh của điểm M qua phép đối xứng tâm I có tọa độ

A. (2; 1)         B. (-1; 5)

C. (-1; 3)        D. (5; -4)

Phương pháp giải:

Sử dụng công thức tọa độ của phép đối xứng tâm \(\left\{ \begin{array}{l}x' = 2{x_I} - x\\y' = 2{y_I} - y\end{array} \right.\)

Hướng dẫn giải:

Gọi \(M' = {D_I}\left( M \right)\), khi đó 

\(\left\{ \begin{array}{l}x' = 2{x_I} - x\\y' = 2{y_I} - y\end{array} \right. \\ \Rightarrow \left\{ \begin{array}{l}x' = 2.1 - 3 = - 1\\y' = 2.2 - \left( { - 1} \right) = 5\end{array} \right. \)

Vậy chọn B.

Trong mặt phẳng (Oxy) cho đường thẳng \(\Delta \) có phương trình x = 2. Ảnh của \(\Delta \) qua phép đối xứng tâm O là đường thẳng

A. x = - 2          B. y = 2

C. x = 2           D. y = - 2

Phương pháp giải:

- Viết dạng của phương trình \(\Delta ' \)(chú ý \(\Delta '//\Delta \)).

- Lấy một điểm \(A \in \Delta\). Tìm ảnh A' của A qua \({D_O}\).

- Cho \(A' \in \Delta '\) suy ra phương trình cần tìm.

Hướng dẫn giải:

Gọi \(\Delta '\) là ảnh của \(\Delta \) qua \({D_O}\), dễ thấy \(O \notin \Delta \) nên \(\Delta '//\Delta \) hay \(\Delta ':x = c\)

Lấy \(A\left( {2;0} \right) \in \Delta\), gọi \(A' = {D_O}\left( A \right) \) thì A'(-2; 0)

Do \(A' \in \Delta ' \) nên  - 2 = c.

Vậy chọn A.

Khẳng định nào sau đây là đúng?

A. Phép đối xứng tâm không có điểm nào biến thành chính nó.

B. Phép đối xứng tâm có đúng một điểm biến thành chính nó.

C. Có phép đối xứng tâm có hai điểm biến thành chính nó.

D. Có phép đối xứng tâm có vô số điểm biến thành chính nó.

Phương pháp giải:

Nhận xét từng đáp án, sử dụng định nghĩa phép đối xứng tâm:

Cho điểm I, phép biến hình biến mỗi điểm I thành chính nó và mỗi điểm \(M \ne I\) thành điểm M' sao cho I là trung điểm MM' được gọi là phép đối xứng tâm.

Hướng dẫn giải:

Phép đối xứng tâm có đúng một điểm biến thành chính nó, đó chính là tâm đối xứng.

Vậy chọn B.

Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) có phương trình x - y + 4 = 0. Đường thẳng \(\Delta \) là ảnh qua một phép đối xứng tâm của đường thẳng

A. 2x + y - 4 = 0

B. x + y - 1 = 0

C. 2x - 2y + 1 = 0

D. 2x + 2y - 3 = 0

Phương pháp giải:

Sử dụng tính chất của phép đối xứng tâm: biến đường thẳng thành đường thẳng song song với nó (trường hợp tâm đối xứng không nằm trên đường thẳng).

Hướng dẫn giải:

Quan sát các đáp án ta chỉ thấy đường thẳng ở đáp án C song song với đường thẳng đã cho vì \(\dfrac{1}{2} = \dfrac{{ - 1}}{{ - 2}} \ne \dfrac{4}{1}.\)

Vậy chọn C.

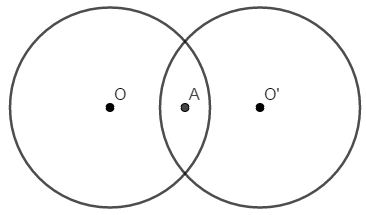
Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?

A. Không có         B. Chỉ có một

C. Chỉ có hai         D. Vô số

Phương pháp giải:

Sử dụng tính chất của tâm đối xứng, biến đường tròn thành đường tròn có cùng bán kính.

Hướng dẫn giải:

Do phép đối xứng tâm biến một đường tròn thành đường tròn có cùng bán kính nên hình gồm hai đường tròn phân biệt cùng bán kính thì có một tâm đối xứng duy nhất là trung điểm đoạn nối tâm.

Vậy chọn B.

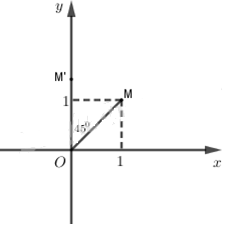
Trong mặt phẳng Oxy cho điểm M(1; 1). Ảnh của M qua phép quay tâm O, góc quay \({45^0}\) có tọa độ

A. (-1; 1)            B. (1; 0)

C. (2; 0)            D. \(\left( {0;\sqrt 2 } \right)\)

Phương pháp giải:

Dựng hình và nhận xét.

Hướng dẫn giải:

Dễ thấy M(1; 1) nằm trên đường phân giác của góc phần tư thứ nhất.

Khi đó 

\(M' = {Q_{\left( {O,{{45}^0}} \right)}}\left( M \right) \Leftrightarrow \left( {OM,OM'} \right) = {45^0}\)

Mên M' nằm trên tia Oy.

Do đó \(M'\left( {0;m} \right)\) với m > 0.

Lại có 

\(OM = OM'\\ \Leftrightarrow \sqrt 2 = \sqrt {0 + {m^2}}\\ \Leftrightarrow m = \sqrt 2.\)

Suy ra \(M'\left( {0;\sqrt 2 } \right).\)

Vậy chọn D.

Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc \(\alpha,0 \le \alpha < 2\pi\), biến tam giác trên thành chính nó?

A. Chỉ có một          B. Chỉ có hai

C. Chỉ có ba           D. Chỉ có bốn

Phương pháp giải:

Dựa vào tính chất của tam giác đều và nhận xét.

Hướng dẫn giải:

Ta có:

 \({Q_{\left( {O,0} \right)}}\left( A \right) = A, {Q_{\left( {O,0} \right)}}\left( B \right) = B, {Q_{\left( {O,0} \right)}}\left( C \right) = C \) nên \({Q_{\left( {O,0} \right)}}\)biến tam giác ABC thành chính nó.

 \({Q_{\left( {O,\dfrac{{2\pi }}{3}} \right)}}\left( A \right) = B, {Q_{\left( {O,\dfrac{{2\pi }}{3}} \right)}}\left( B \right) = C, {Q_{\left( {O,\dfrac{{2\pi }}{3}} \right)}}\left( C \right) = A\) nên \({Q_{\left( {O,\dfrac{{2\pi }}{3}} \right)}}\) biến tam giác ABC thành tam giác BCA hay chính nó.

\({Q_{\left( {O,\dfrac{{4\pi }}{3}} \right)}}\left( A \right) = C, {Q_{\left( {O,\dfrac{{4\pi }}{3}} \right)}}\left( B \right) = A, {Q_{\left( {O,\dfrac{{4\pi }}{3}} \right)}}\left( C \right) = B\) nên \({Q_{\left( {O,\dfrac{{4\pi }}{3}} \right)}}\) biến tam giác ABC thành tam giác CAB hay chính nó.

Vậy có 3 phép quay cần tìm.

Vậy chọn C.

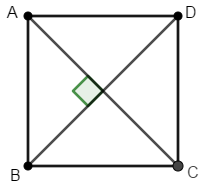
Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc \(\alpha, 0 \le \alpha < 2\pi\), biến hình vuông trên thành chính nó?

A. Chỉ có một          B. Chỉ có hai

C. Chỉ có ba           D. Chỉ có bốn

Phương pháp giải:

Dựa vào tính chất của hình vuông và nhận xét.

Hướng dẫn giải:

Ta có:

\({Q_{\left( {O,0} \right)}}\left( A \right) = A, {Q_{\left( {O,0} \right)}}\left( B \right) = B, {Q_{\left( {O,0} \right)}}\left( C \right) = C, {Q_{\left( {O,0} \right)}}\left( D \right) = D\)

Do đó \({Q_{\left( {O,0} \right)}}\left( {ABCD} \right) = ABCD.\)

\({Q_{\left( {O,\dfrac{\pi }{2}} \right)}}\left( A \right) = B, {Q_{\left( {O,\dfrac{\pi }{2}} \right)}}\left( B \right) = C, {Q_{\left( {O,\dfrac{\pi }{2}} \right)}}\left( C \right) = D, {Q_{\left( {O,\dfrac{\pi }{2}} \right)}}\left( D \right) = A\)

Do đó \({Q_{\left( {O,\dfrac{\pi }{2}} \right)}}\left( {ABCD} \right) = BCDA.\)

\({Q_{\left( {O,\pi } \right)}}\left( A \right) = C, {Q_{\left( {O,\pi } \right)}}\left( B \right) = D, {Q_{\left( {O,\pi } \right)}}\left( C \right) = A, {Q_{\left( {O,\pi } \right)}}\left( D \right) = B\)

Do đó \({Q_{\left( {O,\dfrac{\pi }{2}} \right)}}\left( {ABCD} \right) = CDAB.\)

\({Q_{\left( {O,\dfrac{{3\pi }}{2}} \right)}}\left( A \right) = D, {Q_{\left( {O,\dfrac{{3\pi }}{2}} \right)}}\left( B \right) = A, {Q_{\left( {O,\dfrac{{3\pi }}{2}} \right)}}\left( C \right) = B, {Q_{\left( {O,\dfrac{{3\pi }}{2}} \right)}}\left( D \right) = C\)

Do đó \({Q_{\left( {O,\dfrac{\pi }{2}} \right)}}\left( {ABCD} \right) = DABC.\)

Suy ra có 4 phép quay cần tìm.

Vậy chọn D.

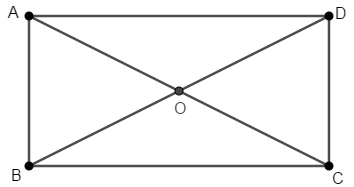
Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc \(\alpha,0 \le \alpha < 2\pi\), biến hình chữ nhật trên thành chính nó?

A. Không có          B. Chỉ có hai

C. Chỉ có ba          D. Chỉ có bốn

Phương pháp giải:

Vẽ hình và nhận xét.

Hướng dẫn giải:

Ta có:

\({Q_{\left( {O,0} \right)}}\left( A \right) = A, {Q_{\left( {O,0} \right)}}\left( B \right) = B, {Q_{\left( {O,0} \right)}}\left( C \right) = C, {Q_{\left( {O,0} \right)}}\left( D \right) = D\)

Nên \({Q_{\left( {O,0} \right)}}\left( {ABCD} \right) = ABCD.\)

\( {Q_{\left( {O,\pi } \right)}}\left( A \right) = C, {Q_{\left( {O,\pi } \right)}}\left( B \right) = D, {Q_{\left( {O,\pi } \right)}}\left( C \right) = A, {Q_{\left( {O,\pi } \right)}}\left( D \right) = B\)

Nên \({Q_{\left( {O,0} \right)}}\left( {ABCD} \right) = CDAB.\)

Suy ra có 2 phép quay cần tìm.

Vậy chọn B.

Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc quay \(\alpha \ne k2\pi,\) k là một số nguyên?

A. Không có              B. Chỉ có một

C. Chỉ có hai              D. Vô số

Phương pháp giải:

Sử dụng định nghĩa phép quay:

Phép quay tâm O góc quay \(\alpha \) là phép biến hình biến điểm O thành chính nó và biến mỗi điểm M khác O thành điểm M' sao cho OM' = OM và \(\left( {OM,OM'} \right) = \alpha.\)

Hướng dẫn giải:

Do \(\alpha \ne k2\pi \) nên với mỗi \(M \ne O\) thì \(M' \ne M.\)

Nếu \(M \equiv O\) thì theo định nghĩa phép quay ta thấy, phép quay tâm O biến O thành chính nó.

Do đó chỉ có 1 điểm duy nhất.

Vậy chọn B.

Trong mặt phẳng Oxy cho điểm M(2; 1). Điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo véctơ \(\overrightarrow v \left( {2;3} \right)\) được biến thành điểm có tọa độ

A. (1; 3)            B. (2; 0)

C. (0; 2)           D. (4; 4)

Phương pháp giải:

- Tìm ảnh M' của M qua phép đối xứng tâm O.

- Tìm ảnh của M' qua phép tịnh tiến theo véctơ \(\overrightarrow v.\)

Hướng dẫn giải:

Gọi \(M' = {D_O}\left( M \right)\) thì \(\left\{ \begin{array}{l}x' = - x\\y' = - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = - 2\\y' = - 1\end{array} \right.\) hay \(M'\left( { - 2; - 1} \right).\)

Gọi \(M'' = {T_{\overrightarrow v }}\left( {M'} \right)\) thì \(\left\{ \begin{array}{l}x'' = x' + 2 = - 2 + 2 = 0\\y'' = y' + 3 = - 1 + 3 = 2\end{array} \right.\) hay \(M''\left( {0;2} \right)\).

Vậy chọn C.

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\). Đường tròn (C) qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo véctơ \(\overrightarrow v \left( {2;3} \right)\) được biến thành đường tròn có phương trình

A. \({x^2} + {y^2} = 4 \)

B. \({\left( {x - 2} \right)^2} + {\left( {y - 6} \right)^2} = 4\)

C. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 4\)

D. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4\)

Phương pháp giải:

- Tìm tâm I và bán kính R của đường tròn đã cho.

- Tìm ảnh I' của I qua phép đối xứng trục Oy.

- Tìm ảnh của I' qua phép tịnh tiến theo véctơ \(\overrightarrow v.\)

- Viết phương trình đường tròn, chú ý đường tròn mới có bán kính bằng bán kính đường tròn ban đầu.

Hướng dẫn giải:

Đường tròn (C) có tâm I(1; -2) và bán kính R = 2.

Gọi \(I' = {D_{Oy}}\left( I \right)\) thì \(\left\{ \begin{array}{l}x' = - x = - 1\\y' = y = - 2\end{array} \right.\) hay I'(-1; -2).

Gọi \(I'' = {T_{\overrightarrow v }}\left( {I'} \right)\) thì \(\left\{ \begin{array}{l}x'' = x' + 2 = - 1 + 2 = 1\\y'' = y' + 3 = - 2 + 3 = 1\end{array} \right.\) hay \(I''\left( {1;1} \right)\).

Đường tròn ảnh có cùng bán kính với đường tròn đã cho nên có phương trình: \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4.\)

Vậy chọn D.

Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Đường thẳng d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo véctơ \(\overrightarrow v \left( {3;2} \right)\) được biến thành đường thẳng có phương trình

A. 3x + 3y - 2 = 0

B. x - y + 2 = 0

C. x + y + 2 = 0

D. x + y - 3 = 0

Phương pháp giải:

- Gọi phương trình đường thẳng d'' là ảnh của d qua phép dời hình đã cho (chú ý d'' song song hoặc trùng d)

- Lấy một điểm A bất kì thuộc d, tìm ảnh A'' của điểm này qua hai phép dời hình trên.

- Cho \(A'' \in d''\) và kết luận.

Hướng dẫn giải:

Gọi d'' là đường thẳng cần tìm thì d'': x + y + c = 0.

Lấy \(A\left( {0;2} \right) \in d\), gọi \(A' = {D_O}\left( A \right)\) thì \(\left\{ \begin{array}{l}x' = - x = 0\\y' = - y = - 2\end{array} \right.\) hay \(A'\left( {0; - 2} \right).\)

Gọi \(A'' = {T_{\overrightarrow v }}\left( {A'} \right)\) thì \(\left\{ \begin{array}{l}x'' = x' + 3 = 0 + 3 = 3\\y'' = y' + 2 = - 2 + 2 = 0\end{array} \right.\) hay \(A''\left( {3;0} \right).\)

Mà \(A'' \in d''\) nên \(3 + 0 + c = 0 \Leftrightarrow c = - 3.\)

Vậy d'': x + y - 3 = 0.

Vậy chọn D.

Khẳng định nào sau đây đúng?

A. Thực hiện liên tiếp hai phép tịnh tiến sẽ được một phép tịnh tiến.

B. Thực hiện liên tiếp hai phép đối xứng trục sẽ được một phép đối xứng trục.

C. Thực hiện liên tiếp phép đối xứng qua tâm và phép đối xứng trục sẽ được một phép đối xứng qua tâm.

D. Thực hiện liên tiếp phép quay và phép tịnh tiến sẽ được một phép tịnh tiến.

Phương pháp giải:

Xem lại tính chất các phép biến hình và kết luận tính đúng sai của từng đáp án.

Chú ý chỉ ra phản ví dụ cho đáp án sai.

Hướng dẫn giải:

Đáp án A: Đúng vì hợp thành của hai phép tịnh tiến là một phép tịnh tiến có véc tơ tịnh tiến bằng tổng hai véc tơ tịnh tiến.

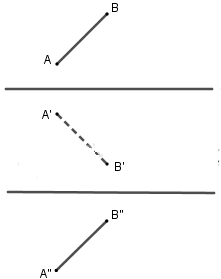
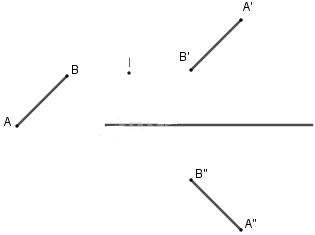
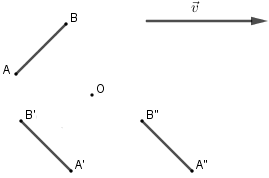
Đáp án B: Sai, quan sát hình vẽ ta thấy không có phép đối xứng trục nào biến đoạn thẳng AB thành A''B''.

Đáp án C: sai, quan sát hình vẽ ta thấy không có phép đối xứng tâm nào biến đoạn AB thành A''B''.

Đáp án D: sai, quan sát hình vẽ ta thấy không có phép tịnh tiến nào biến đoạn AB thành A''B''.

Vậy chọn A.

Khẳng định nào sau đây đúng?

A. Có một phép tịnh tiến theo véc tơ khác không biến mọi điểm thành chính nó.

B. Có một phép đối xứng trục biến mọi điểm thành chính nó.

C. Có một phép đối xứng tâm biến mọi điểm thành chính nó.

D. Có một phép quay biến mọi điểm thành chính nó.

Phương pháp giải:

Xét tính đúng sai của từng đáp án và kết luận.

Hướng dẫn giải:

Đáp án A: Chỉ có một phép tịnh tiến theo véc tơ \overrightarrow 0  biến mọi điểm thành chính nó. Nên A sai.

Đáp án B: Sai vì phép đối xứng trục chỉ biến các điểm thuộc trục đối xứng thành chính nó, các điểm khác thì không.

Đáp án C: Sai vì phép đối xứng tâm chỉ biến tâm đối xứng thành chính nó, các điểm khác thì không.

Đáp án D: Đúng vì phép quay tâm O góc quay k2\pi,k \in \mathbb{Z} biến mọi điểm thành chính nó.

Vậy chọn D.