Giải bài tập SBT Toán 11 Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
Nội dung giải SBT môn Toán lớp 11 trang 80 được eLib biên soạn và tổng hợp bên dưới đây sẽ giúp các em học sinh học vừa ôn tập kiến thức vừa củng cố kĩ năng làm bài. Thông qua hệ thống 5 bài tập có hướng dẫn giải chi tiết để các em có thể đối chiếu với bài làm của mình từ đó có kế hoạch học tập phù hợp. Mời các em cùng tham khảo.
Mục lục nội dung

1. Giải bài 2.32 trang 80 SBT Hình học 11
Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau hay không?
Hình chiếu song song của hai đường thẳng cắt nhau có song song với nhau hay không?
Phương pháp giải:
Sử dụng tính chất: Hai măt phẳng song song với nhau. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Hướng dẫn giải:
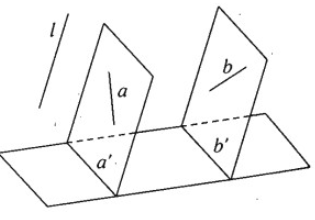
Giả sử a và b là hai đường thẳng chéo nhau có hình chiếu là a’ và b’.
Nếu mặt phẳng (a, a’) và mặt phẳng (b, b’) song song với nhau thì a' // b'.
Vậy hình chiếu song song của hai đường thẳng chéo nhau có thể song song.
Nếu a và b là hai đường thẳng cắt nhau tại O và hình chiếu của O là O’ thì \(O' \in a'\) và \(O' \in b'\) tức là a’ và b’ có điểm chung.
Vậy hình chiếu song song của hai đường thẳng cắt nhau không thể song song được.
2. Giải bài 2.33 trang 80 SBT Hình học 11
Trong mặt phẳng \(\left( \alpha \right)\) cho một tam giác ABC bất kì. Chứng minh rằng có thể xem tam giác ABC là hình chiếu song song của một tam giác đều nào đó.
Phương pháp giải:
Sử dụng khái niệm hình chiếu song song của một điểm.
Hướng dẫn giải:
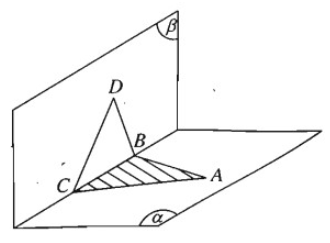
Cho tam giác ABC bất kì nằm trong mặt phẳng \(\left( \alpha \right)\).
Gọi \(\left( \beta \right)\) là mặt phẳng qua BC và khác với \(\left( \alpha \right)\).
Trong \(\left( \beta \right)\) ta vẽ tam giác đều BCD.
Vậy ta có thể xem tam giác ABC cho trước là hình chiếu song song của tam giác đều DBC theo phương chiếu DA lên mặt phẳng \(\left( \alpha \right)\).
3. Giải bài 2.34 trang 80 SBT Hình học 11
Vẽ hình biểu diễn của một hình lục giác đều.
Phương pháp giải:
Áp dụng tính chất:
- Một hình bình hình bất kỳ có thể coi là hình biểu diễn của một hình bình hành tùy ý cho trước (có thể là hình bình hành, hình vuông, hình chữ nhật, hình thoi...).
- Hình lục giác đều có tâm đối xứng là giao điểm của các đường chéo.
- Tính chất đối xứng tâm.
Hướng dẫn giải:
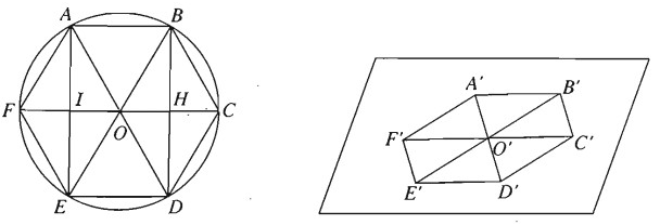
Với hình lục giác đều ABCDEF ta nhận thấy:
- Tứ giác OABC là hình bình hành (vừa là hình thoi);
- Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua tâm O.
Từ đó suy ra cách vẽ hình biểu diễn của lục giác đều ABCDEF như sau:
- Vẽ hình bình hành O’A’B’C’ biểu diễn cho hình bình hành OABC.
- Lấy các điểm D’, E’, F’ lần lượt đối xứng của A’, B’, C’ qua tâm O’, ta được hình biểu diễn A’B’C’D’E’F’ của hình lục giác đều ABCDEF.
4. Giải bài 2.35 trang 80 SBT Hình học 11
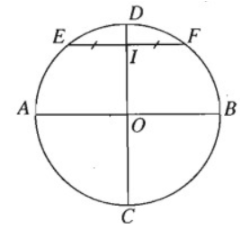
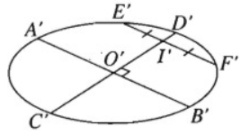
Hãy vẽ hình biểu diễn của một đường tròn cùng với hai đường kính vuông góc của đường tròn đó.
Phương pháp giải:
Áp dụng tính chất:
- Hình elip để biểu diễn hình tròn.
- Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó. Bảo toàn tỉ số của điểm chia đoạn.
Hướng dẫn giải:
Giả sử trên hình thực ta có đường tròn tâm O cùng với hai đường kính vuông góc của đường tròn đó là AB và CD.
Ta vẽ thêm một dây cung EF song song với AB.
Khi đó đường kính CD sẽ đi qua trung điểm I của đoạn EF.
Từ đó ta suy ra cách vẽ sau đây:
- Vẽ hình elip biểu diễn cho đường tròn và vẽ đường kính A’B’ của hình elip đó. Đường kính này đi qua tâm O’ của elip.
- Vẽ một dây cung E’F’ song song với đường kính A’B’.
- Gọi I’ là trung điểm của E’F’. Đường thẳng O’I’ cắt elip tại hai điểm C’ và D’. Ta có A’B’ và C’D’ là hình biểu diễn của hai đường kính vuông góc với nhau của đường tròn.
5. Giải bài 2.36 trang 80 SBT Hình học 11
Hãy chọn phép chiếu song song với phương chiếu và mặt phẳng chiếu thích hợp để hình chiếu song song của một tứ diện cho trước là một hình bình hành.
Phương pháp giải:
Ápử dụng tính chất: Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó. Bảo toàn tỉ số của điểm chia đoạn.
Hướng dẫn giải:
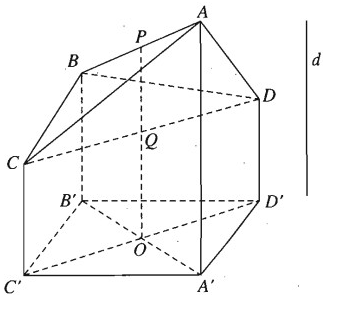
Cho tứ diện ABCD.
Gọi d là một đường thẳng không song song với với các cạnh của tứ diện và \(\left( \alpha \right)\) là một mặt phẳng cắt d.
Gọi A’, B’, C’, D’ lần lượt là hình chiếu của A, B, C, D trên mặt phẳng \(\left( \alpha \right)\).
Gọi P và Q lần lượt là trung điểm của hai cạnh đối diện AB và CD.
Khi đó hình chiếu của P’ và Q’ của P và Q sẽ lần lượt là trung điểm của A’B’ và C’D’.
Muốn cho A’, B’, C’, D’ là các đỉnh của một hình bình hành ta chỉ cần chọn phương chiếu d sao cho d song song với đường thẳng PQ.
Vậy để hình chiếu song song của một tứ diện là một hình bình hành ta có thể chọn:
- Phương chiếu d là phương của một trong ba đường thẳng đi qua trung điểm của hai cạnh đối diện của tứ diện cho trước.
- Mặt phẳng chiếu \(\left( \alpha \right)\) là mặt phẳng tùy ý, nhưng phải cắt đường thẳng d.
Tham khảo thêm
- doc Giải bài tập SBT Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng
- doc Giải bài tập SBT Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- doc Giải bài tập SBT Toán 11 Bài 3: Đường thẳng và mặt phẳng song song
- doc Giải bài tập SBT Toán 11 Bài 4: Hai mặt phẳng song song
- doc Giải bài tập SBT Hình học 11 Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song