Giải bài tập SBT Toán 12 Bài 1: Số phức, biểu diễn hình học số phức
Mời các em học sinh cùng tham khảo nội dung giải bài tập bài Số phức, biểu diễn hình học số phức trang 198, 199 SBT Toán 12 bên dưới đây. Đây là tài liệu hữu ích vừa giúp các em ôn tập kiến thức đã học vừa củng cố kĩ năng làm bài tập hiệu quả thông qua hệ thống các bài tập có phương pháp và lời giải chi tiết sau đây.
Mục lục nội dung

1. Giải bài 4.1 trang 198 SBT Giải tích 12
Tìm các số thực \(x, y\) thỏa mãn:
\(a) 2x+1+(1-2y)i=2-x+(3y-2)i\\ b) 4x+3+(3y-2)i=y+1+(x-3)i\\ c) x+2y+(2x-y)i=2x+y+(x+2y)i\)
Phương pháp giải
\(a+bi=a'+b'i\Leftrightarrow \left\{ \begin{aligned} & a=a' \\ & b=b' \\ \end{aligned} \right. \)
Hướng dẫn giải
a)
\(\left\{ \begin{aligned} & 2x+1=2-x \\ & 1-2y=3y-2 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & x=\dfrac{1}{3} \\ & y=\dfrac{3}{5} \\ \end{aligned} \right.\)
b)
\(\left\{ \begin{aligned} & 4x+3=y+1 \\ & 3y-2=x-3 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & 4x-y=-2 \\ & x-3y=1 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & x=-\dfrac{7}{11} \\ & y=-\dfrac{6}{11} \\ \end{aligned} \right. \)
c)
\(\left\{ \begin{aligned} & x+2y=2x+y \\ & 2x-y=x+2y \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & x=-y \\ & x=y \\ \end{aligned} \right.\Leftrightarrow x=y=0 \)
2. Giải bài 4.2 trang 198 SBT Giải tích 12
Cho hai số phức \( \alpha =a+bi,\,\beta =c+di \). Hãy tìm điều kiện của \(a, b, c, d\) để các điểm biểu diễn \(\alpha\) và \(\beta\) trên mặt phẳng tọa độ :
a) Đối xứng với nhau qua trục \(Ox\)
b) Đối xứng với nhau qua trục \(Oy\)
c) Đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất và góc phần tư thứ ba
d) Đối xứng với nhau qua gốc tọa độ.
Phương pháp giải
Hai điểm đối xứng với nhau qua trục Ox nếu x = x', y = - y'
Hai điểm đối xứng với nhau qua trục Oy nếu x = - x', y = y'
Hai điểm đối xứng với nhau qua đường thẳng y = x nếu x = y', y = x'
Hai điểm đối xứng với nhau qua gốc tọa độ O nếu x = - x', y = - y'
Hướng dẫn giải
Điểm biểu diễn số phức \(\alpha =a+bi\) là \(\left( a;b \right) \)
Điểm biểu diễn số phức \(\beta =c+di\) là \(\left( c;d \right) \)
a) Hai điểm đối xứng với nhau qua \(Ox\) nếu:
\(\left\{ \begin{aligned} & a=c \\ & b=-d \\ \end{aligned} \right. \)
b) Hai điểm đối xứng với nhau qua \(Oy\) nếu:
\(\left\{ \begin{aligned} & a=-c \\ & b=d \\ \end{aligned} \right. \)
c) Đường phân giác góc phần tư thứ nhất và góc phần tư thứ ba là \(y=x\)
Để hai điểm biểu diễn đối xứng nhau qua đường thẳng \(y=x\) là:
\(\left\{ \begin{aligned} & a=d \\ & b=c \\ \end{aligned} \right.\)
d) Đối xứng nhau qua gốc tọa độ nếu :
\(\left\{ \begin{aligned} & a=-c \\ & b=-d \\ \end{aligned} \right. \)
3. Giải bài 4.3 trang 199 SBT Giải tích 12
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện:
a) Phần thực của \(z\) bằng phần ảo của nó
b) Phần thực của \(z\) là số đối của phần ảo của nó
c) Phần ảo của \(z\) bằng hai lần phần thực của nó cộng với 1
d) Modun của \(z\) bằng 1, phần thực của \(z\) không âm.
Phương pháp giải
Đặt z = x + yi, tìm mối quan hệ x, y và suy ra đáp số.
Hướng dẫn giải
Gọi số phức \(z\) là \(x+yi\) trong đó \(x,y\in \mathbb{R} \)
a) Phần thực bằng phần ảo : \(x=y \)
Tập hợp số phức là đường phân giác góc phần tư thứ nhất và góc phần tư thứ ba.
b) Phần thực là số đối của phần ảo : \(x=-y \)
Tập hợp số phức là đường phân giác góc phần tư thứ hai và góc phần tư thứ tư.
c) Phần ảo bằng hai lần phần thực của nó cộng với 1 : \(y=2x+1.\)
Tập hợp số phức là đường thẳng \(y=2x+1\)
d) Môđun của nó là 1, phần thực của z không âm: \({{x}^{2}}+{{y}^{2}}=1,\,\,\,\left( x>0 \right) \)
Tập hợp số phức là nửa đường tròn tâm O bán kính bằng 1, nằm bên phải trục Oy
4. Giải bài 4.4 trang 199 SBT Giải tích 12
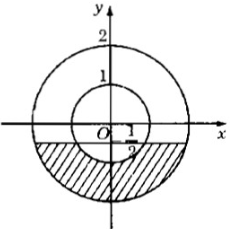
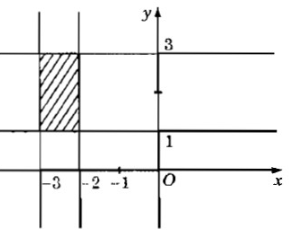
ố phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình 4.2 và hình 4.3?
Phương pháp giải
Quan sát hình vẽ và nhận xét phần thực và phần ảo của số phức z.
Hướng dẫn giải
Gọi số phức là: \(z=x+yi ,\,\,\,x,y\in \mathbb R\)
Hình 4.2.
\(\left\{ \begin{aligned} & -3< x<-2 \\ & 1< y<3 \\ \end{aligned} \right. \)
Hình 4.3.
\(1\le {{x}^{2}}+{{y}^{2}}\le 2,\,\,y\le -\dfrac{1}{2}\,\, \)
5. Giải bài 4.5 trang 199 SBT Giải tích 12
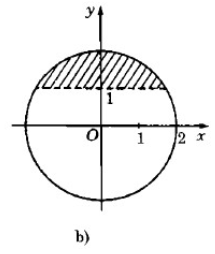
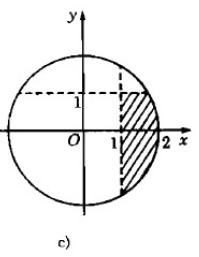
Hãy biểu diễn các số phức \(z\) trên mặt phẳng tọa độ, biết \( |z| ≤ 2\) và:
a) Phần thực của \(z\) không vượt quá phần ảo của nó
b) Phần ảo của \(z\) lớn hơn 1
c) Phần ảo của \(z\) nhỏ hơn 1, phần thực của \(z\) lớn hơn 1.
Phương pháp giải
Dựng đường tròn \({x^2} + {y^2} = 4\) và suy ra phần mặt phẳng biểu diễn các số phức theo yêu cầu.
Hướng dẫn giải
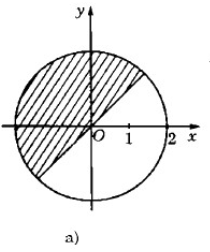
6. Giải bài 4.6 trang 199 SBT Giải tích 12
Cho \(z\in \mathbb{C}\). Mệnh đề nào sau đây sai?
A. Nếu \(z\in \mathbb{R}\) thì \(z=\overline{z} \)
B. Nếu \(z=\overline{z} \) thì \(z\in \mathbb{R}\)
C. Nếu \(z\in \mathbb{R}\) thì \(z=\left| z \right|\)
D. Nếu \(z=\left| z \right|\) thì \(z\in \mathbb{R}\)
Phương pháp giải
Số phức z là số thực nếu phần ảo của nó bằng 0
Hướng dẫn giải
Gọi số phức \(z=a+bi,\,\,\,a,b\in \mathbb{R} \)
A. Vì \( z\in \mathbb{R}\Rightarrow b=0 \)nên \(z=\overline{z}\). A đúng
B. \(z=a+bi,\,\overline{z}=a-bi \)
Nếu \(z=\overline{z}\Rightarrow a+bi=a-bi\Leftrightarrow b=0 \)hay \(z\in \mathbb{R}\). B đúng
C. \(z\in \mathbb{R}\Rightarrow z=a\Leftrightarrow \left| z \right|=\left| a \right|\ne z\). C sai
D. \(z=\left| z \right|\Leftrightarrow a+bi=\sqrt{{{a}^{2}}+{{b}^{2}}}\Leftrightarrow b=0\Rightarrow z\in \mathbb{R}\). D đúng
Chọn C.
7. Giải bài 4.7 trang 200 SBT Giải tích 12
Cho \(z\in \mathbb{C}\). Mệnh đề nào sau đây đúng?
A. Nếu \(z\in \mathbb{C}\backslash \mathbb{R}\) thì \(z\) là một số thuần ảo.
B. Nếu \(z\) là một số thuần ảo thì \(z\in \mathbb{C}\backslash \mathbb{R}\)
C. Nếu \(z\) là một số thuần ảo thì \(z=\left| z \right|\)
D. Nếu \(z\) là một số thuần ảo thì \(z=\overline{z}\)
Phương pháp giải
Nhận xét tính đúng sai của từng đáp án, sử dụng định nghĩa số thuần ảo là số phức có phần thực bằng 0.
Hướng dẫn giải
Đáp án A sai vì vẫn có thể xảy ra trường hợp z = a + bi với \(a \ne 0,b \ne 0\)
Đáp án C sai vì nếu z = i thì \(i \ne \left| i \right| = 1\)
Đáp án D sai vì nếu z là số thuần ảo thì z = bi nên \(\overline z = - bi \ne z\)
Trong các đáp án đã cho thì có đáp án B là chính xác hơn.
Chọn B.
Các em hãy luyện tập bài trắc nghiệm Số phức, biểu diễn hình học số phức Toán 12 sau để nắm rõ thêm kiến thức bài học.
Tham khảo thêm
- doc Giải bài tập SBT Toán 12 Bài 2: Phép cộng và nhân các số phức
- doc Giải bài tập SBT Toán 12 Bài 3: Phép chia số phức
- doc Giải bài tập SBT Toán 12 Bài 4: Phương trình bậc hai với hệ số thực