Giải bài tập SBT Toán 12 Bài 3: Ứng dụng hình học của tích phân

Tính diện tích hình phẳng giới hạn bởi các đường sau:

a) \(y= 2 x - x^2, x+y=2\);

b) \(y=x^3-12 x, y=x^2\);

c) \(x+y=1, x+y=-1, x-y=1, x-y=-1\);

d) \(y=\dfrac{1}{1+x^2}, y=\dfrac{1}{2}\);

e) \(y=x^3-1\) và tiếp tuyến với  \(y=x^3-1\) tại điểm (-1;-2).

Phương pháp giải

- Giải phương trình hoành độ giao điểm của hai đồ thị hàm số.

- Nếu hình phẳng được giới hạn bởi đồ thị của hàm số f(x) liên tục trên [a;b], trục hoành và hai đường thẳng \(x=a, x=b\) thì diện tích S cho bởi công thức:

\(S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}\)

Hướng dẫn giải

a) Hoành độ giao điểm của hai đồ thị hàm số \(y= 2 x -x^2; y=-x+2\) là:

\(2 x-x^2=-x+2\)

\(\Leftrightarrow {{x}^{2}}-3x+2=0\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=2 \\ \end{align} \right. \)

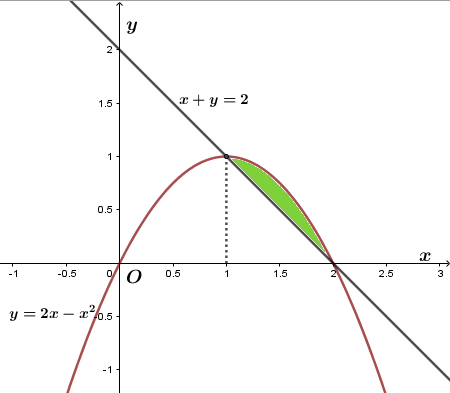
Vậy diện tích S của hình phẳng bằng

\(\begin{aligned} & S=\int\limits_{1}^{2}{\text{ }\!\![\!\!\text{ }(2x-x\hat{\ }2)-(-x+2)\text{ }\!\!]\!\!\text{ dx}} \\ & \,\,\,=\int\limits_{1}^{2}{\left( 3x-{{x}^{2}}-2 \right)\text{dx}} \\ & \,\,\,=\left( \frac{3}{2}{{x}^{2}}-\frac{{{x}^{3}}}{3}-2x \right)\left| \begin{aligned} & 2 \\ & 1 \\ \end{aligned} \right. \\ & \,\,\,=\frac{1}{6} \text{(đvdt)}\\ \end{aligned} \)

b) Hoành độ giao điểm của hai đồ thị hàm số \(y=x^3-12 x, y=x^2\) là:

\(x^3-12x=x^2\\\Leftrightarrow x^3 -{{x}^{2}}-12x=0\\\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=4 \\ & x=-3 \\ \end{align} \right. \)

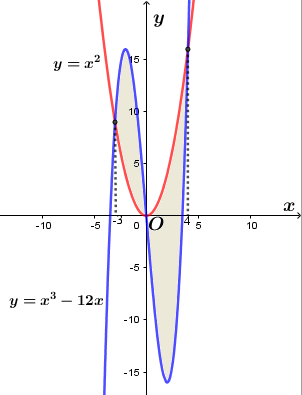
Vậy diện tích S của hình phẳng bằng

\(\begin{aligned} & S=\int\limits_{-3}^{0}{\left( {{x}^{3}}-12x-{{x}^{2}} \right)dx}+\int\limits_{0}^{4}{\left( {{x}^{2}}-{{x}^{3}}+12x \right)dx} \\ & \,\,\,=\left( \frac{{{x}^{4}}}{4}-6{{x}^{2}}+\frac{{{x}^{3}}}{3} \right)\left| \begin{aligned} & 0 \\ & -3 \\ \end{aligned} \right.+\left( \frac{{{x}^{3}}}{3}-\frac{{{x}^{4}}}{4}+6{{x}^{2}} \right)\left| \begin{aligned} & 4 \\ & 0 \\ \end{aligned} \right. \\ & \,\,\,=\frac{99}{4}+\frac{160}{3} \\ & \,\,\,=\frac{937}{12} \text{(đvdt)} \\ \end{aligned} \)

c) Ta có đồ thị của 4 hàm số đã cho:

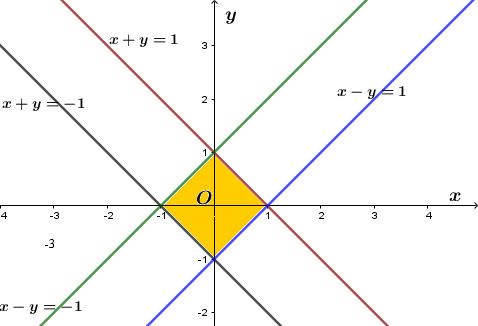
Khi đó diện tích hình phẳng S bằng
\(S=4\int\limits_{0}^{1}{\left( 1-x \right)dx}=4\left( x-\dfrac{{{x}^{2}}}{2} \right)\left| \begin{align} & 1 \\ & 0 \\ \end{align} \right.=2 \text{(đvdt)} \)

d) Hoành độ giao điểm của đồ thị hai hàm số \(y=\dfrac{1}{1+x^2}, y=\dfrac{1}{2}\) là:

\(\dfrac{1}{1+{{x}^{2}}}=\dfrac{1}{2}\Leftrightarrow {{x}^{2}}+1=2\Leftrightarrow {{x}^{2}}=1\Leftrightarrow x=\pm 1\)

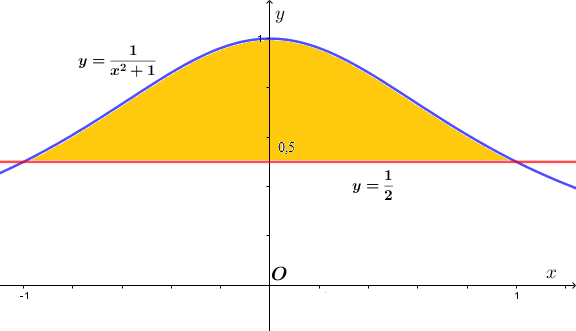
\(\begin{aligned} & S=\int\limits_{-1}^{1}{\left( \frac{1}{1+{{x}^{2}}}-\frac{1}{2} \right)dx}=2\int\limits_{0}^{1}{\left( \frac{1}{1+{{x}^{2}}}-\frac{1}{2} \right)dx} \\ & \,\,\,=2\left( \arg \tan x-\frac{1}{2}x \right)\left| \begin{aligned} & 1 \\ & 0 \\ \end{aligned} \right. \\ & \,\,\,=2\left( \frac{\pi }{4}-\frac{1}{2} \right) \\ & \,\,\,=\frac{\pi }{2}-1 \,\text{(đvdt)}\\ \end{aligned} \)

e) Phương trình tiếp tuyến tại \((-1; -2)\) là \(y = 3x + 1\)

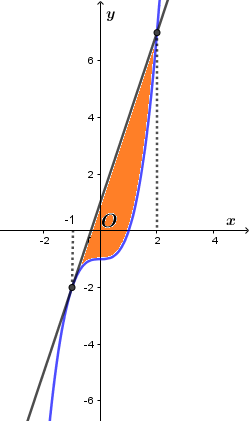
Diện tích S của hình phẳng bằng

\(\begin{aligned} & S=\int\limits_{-1}^{2}{\left( 3x+1-{{x}^{3}}+1 \right)dx}=\int\limits_{-1}^{2}{\left( -{{x}^{3}}+3x+1 \right)dx} \\ & \,\,\,=\left( -\frac{{{x}^{4}}}{4}+\frac{3{{x}^{2}}}{2}+x \right)\left| \begin{aligned} & 2 \\ & -1 \\ \end{aligned} \right. \\ & \,\,\,=\frac{27}{4} \\ \end{aligned} \)

Tính thể tích vật thể:

a) Có đáy là một tam giác cho bởi \(y=x, y=0,x=1\). Mỗi thiết diện vuông góc với trục Ox là một hình vuông.

b) Có đáy là một hình tròn giới hạn bởi \(x^2+y^2=1\). Mỗi thiết diện vuông góc với trục Ox là một hình vuông.

Phương pháp giải

Sử dụng công thức tính thể tích \(\displaystyle V = \int\limits_a^b {S\left( x \right)dx}\)

Hướng dẫn giải

a) Dựng hình:

Thiết diện tại x ∈ [0;1] là hình vuông cạnh bằng x, diện tích thiết diện là \(S(x)=x^2\) .

Khi đó: 

\(V=\int\limits_{0}^{1}{S\left( x \right)dx}=\int\limits_{0}^{1}{{{x}^{2}}dx}=\dfrac{1}{3}\)

b) Dựng hình:

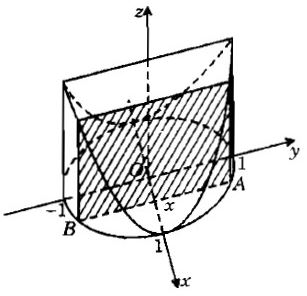
Thiết diện tại x ∈ [-1;1] là hình vuông cạnh AB, trong đó \( A(x; y)\) với \(y=\sqrt{1-x^2}\)

Diện tích thiết diện là: \(S(x) = 4(1 − x^2).\)

Thể tích vật thể là:

\(V=4\int\limits_{-1}^{1}{\left( 1-{{x}^{2}} \right)dx}=8\int\limits_{0}^{1}{\left( 1-{{x}^{2}} \right)dx}=\dfrac{16}{3}\)

Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi

a) \(y=2-x^2, y=1\), quay quanh trục Ox.

b) \(y=2x-x^2, y=x\), quay quanh trục Ox.

c) \(y=(2x+1)^\frac{1}{3}, x=0, y=3\)quay quanh trục Oy.

Phương pháp giải

- Giải phương trình hoành độ giao điểm tìm nghiệm.

- Sử dụng công thức \(\displaystyle  V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \)

Hướng dẫn giải

a)  Ta có: 

\(\begin{aligned} & {{V}_{x}}=\pi \int\limits_{-1}^{1}{{{\left( 2-{{x}^{2}} \right)}^{2}}dx}-\pi \int\limits_{-1}^{1}{dx} \\ & \,\,\,\,\,\,=2\pi \int\limits_{0}^{1}{\left( 4-4{{x}^{2}}+{{x}^{4}} \right)dx}-2\pi \int\limits_{0}^{1}{dx} \\ & \,\,\,\,\,\,=2\pi \left( 4x-\frac{4{{x}^{3}}}{3}+\frac{{{x}^{5}}}{5} \right)\left| \begin{aligned} & 1 \\ & 0 \\ \end{aligned} \right.-2\pi \\ & \,\,\,\,\,\,=\frac{56\pi}{15} \\ \end{aligned} \)

b)

 \(\begin{aligned} & {{V}_{x}}=\pi \int\limits_{0}^{1}{{{\left( 2x-{{x}^{2}} \right)}^{2}}dx}-\pi \int\limits_{0}^{1}{x^2dx} \\ & \,\,\,\,\,\,=\pi \int\limits_{0}^{1}{\left( 4x^2-4{{x}^{3}}+{{x}^{4}} \right)dx}-\pi \int\limits_{0}^{1}{x^2dx} \\ & \,\,\,\,\,\,=\pi \int\limits_{0}^{1}{\left( 3x^2-4{{x}^{3}}+{{x}^{4}} \right)dx} \\ & \,\,\,\,\,\,=\pi \left( x^3-x^4+\frac{{{x}^{5}}}{5} \right)\left| \begin{aligned} & 1 \\ & 0 \\ \end{aligned} \right. \\ & \,\,\,\,\,\,=\frac{\pi}{5} \\ \end{aligned} \)

c) 

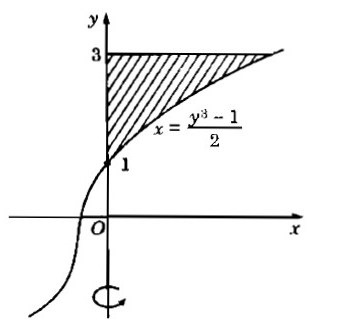
\(\begin{aligned} & {{V}_{y}}=\pi \int\limits_{1}^{3}{{{\left( \frac{{{y}^{3}}-1}{2} \right)}^{2}}dy} \\ & \,\,\,\,\,\,=\frac{\pi }{4}\int\limits_{0}^{1}{\left( {{y}^{6}}-2{{y}^{3}}+1 \right)dy} \\ & \,\,\,\,\,\,=\frac{\pi }{4}\left( \frac{{{y}^{7}}}{7}-\frac{{{y}^{4}}}{2}+y \right)\left| \begin{aligned} & 3 \\ & 1 \\ \end{aligned} \right. \\ & \,\,\,\,\,\,=\frac{480}{7}\pi \\ \end{aligned} \)

Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường \(y=\dfrac{1}{x}, y=0, x=1, x=a\, (a>1).\)

Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi \(a \to +\infty\) (tức là \(\lim\limits_{a\to +\infty }V\left( a \right)\)).

Phương pháp giải

Sử dụng công thức \(\displaystyle V = \pi \int\limits_a^b {{f^2}\left( x \right)dx}\)

Hướng dẫn giải

Ta có:

\(\begin{aligned} & V\left( a \right)=\pi \int\limits_{1}^{a}{\frac{1}{{{x}^{2}}}dx} \\ & \,\,\,\,\,\,=-\frac{\pi }{x}\left| \begin{aligned} & a \\ & 1 \\ \end{aligned} \right. \\ & \,\,\,\,\,\,=\left( 1-\frac{1}{a} \right)\pi \\ \end{aligned} \)

\(\lim\limits_{a\to +\infty }\,V\left( a \right)=\lim\limits_{a\to +\infty }\,\left( 1-\dfrac{1}{a} \right)\pi=\pi\)

Một hình phẳng được giới hạn bởi \(y=e^{-x}, y=0, x=0, x=1\). Ta chia đoạn [0;1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật như Hình 3.9).

a) Tính diện tích \(S_n\) của hình bậc thang (tổng diện tích của n hình chữ nhật con).

b) Tìm \(\underset{n\to \infty }{\mathop{\lim }}\,V_n \)  và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.

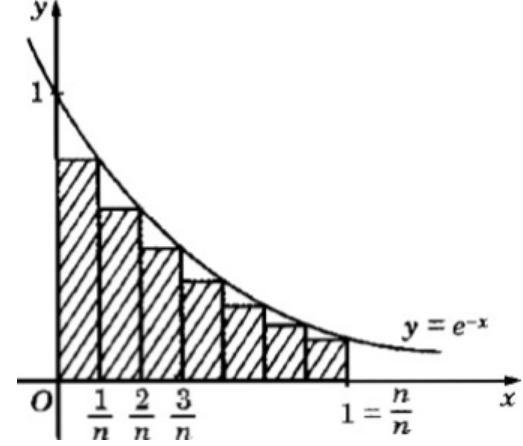
Phương pháp giải

a) Tính diện tích từng hình chữ nhật rồi tính tổng.

b) Tính giới hạn \(\displaystyle \mathop {\lim }\limits_{n \to \infty } {S_n}\) và tính diện tích bằng công thức tích phân \(\displaystyle S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx}\) rồi so sánh.

Hướng dẫn giải

Quan sát hình vẽ ta có: 

a) 

\(\begin{align} & {{S}_{n}}=\frac{1}{n}\left[ {{e}^{-\frac{1}{n}}}+{{e}^{-2\frac{1}{n}}}+...+{{e}^{-\frac{n}{n}}} \right] \\ & \,\,\,\,\,\,=\frac{1}{n}{{e}^{-\frac{1}{n}}}.\frac{1-{{e}^{-1}}}{1-{{e}^{-\frac{1}{n}}}} \\ & \,\,\,\,\,\,=\frac{\frac{1}{n}\left( 1-{{e}^{-1}} \right)}{{{e}^{\frac{1}{n}}}-1} \\ \end{align} \)

b) \(\lim\limits_{a\to +\infty }\,{{S}_{n}}=\lim\limits_{a\to +\infty }\,\dfrac{\dfrac{1}{n}\left( 1-{{e}^{-1}} \right)}{{{e}^{\frac{1}{n}}}-1}=1-{{e}^{-1}}\)

Mặt khác \(\int\limits_{0}^{1}{{{e}^{-x}}dx}=1-{{e}^{-1}}\)

Vậy hai cách tích này đều cho kết quả như nhau.

Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?

a) \(\{y=x+\sin x, y=x, \text{với} \,\,0 \le x \le \pi \}\)và \(\{y=x+\sin x, y=x, \text{với} \,\,\pi \le x \le 2\pi \}\)

b) \(\{y=\sin x, y=0\, \text{với} \,\,\pi \le x \le 2\pi \}\) và  \(\{y=\cos x, y=0\, \text{với} \,\,0 \le x \le \pi \}\)

c) \(\{y=\sqrt{x}, y=0\,\}\) và  \(\{y=\sqrt{1-x^2}, y=1-x\,\}\)

Phương pháp giải

Tính diện tích mỗi cặp hình phẳng đã cho và suy ra kết luận.

Hướng dẫn giải

a) 

Ta có: \(\displaystyle x + \sin x = x \Leftrightarrow \sin x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pi \end{array} \right.\)

Khi đó

\(\displaystyle {S_1} = \int\limits_0^\pi {\left| {x + \sin x - x} \right|dx} \) \(\displaystyle = \int\limits_0^\pi {\left| {\sin x} \right|dx} \) \(\displaystyle = \int\limits_0^\pi {\sin xdx} = - \left. {\cos x} \right|_0^\pi \) \(\displaystyle = - \cos \pi + \cos 0 = 1 + 1 = 2\)

\(\displaystyle {S_2} = \int\limits_\pi ^{2\pi } {\left| {x + \sin x - x} \right|dx} \) \(\displaystyle = \int\limits_\pi ^{2\pi } {\left| {\sin x} \right|dx} \) \(\displaystyle = \int\limits_\pi ^{2\pi } {\left( { - \sin x} \right)dx} = \left. {\cos x} \right|_\pi ^{2\pi }\) \(\displaystyle = \cos 2\pi - \cos \pi = 1 + 1 = 2\)

Do đó \(\displaystyle {S_1} = {S_2}\)

b) 

\(\displaystyle {S_1} = \int\limits_0^\pi {\left| {\sin x} \right|dx} = \int\limits_0^\pi {\sin xdx} \) \(\displaystyle = - \left. {\cos x} \right|_0^\pi \)\(\displaystyle = - \cos \pi + \cos 0 = 1 + 1 = 2\)

\(\displaystyle {S_2} = \int\limits_0^\pi {\left| {\cos x} \right|dx} \) \(\displaystyle = \int\limits_0^{\frac{\pi }{2}} {\left| {\cos x} \right|dx} + \int\limits_{\frac{\pi }{2}}^\pi {\left| {\cos x} \right|dx} \) \(\displaystyle = \int\limits_0^{\frac{\pi }{2}} {\cos xdx} - \int\limits_{\frac{\pi }{2}}^\pi {\cos xdx} \) \(\displaystyle = \left. {\sin x} \right|_0^{\frac{\pi }{2}} - \left. {\sin x} \right|_{\frac{\pi }{2}}^\pi \)

\(\displaystyle = \sin \frac{\pi }{2} - \sin 0 - \sin \pi + \sin \frac{\pi }{2}\) \(\displaystyle = 1 - 0 - 0 + 1 = 2\)

Do đó \(\displaystyle {S_1} = {S_2}\)

c) 

Ta có:

\(\displaystyle \sqrt x = {x^2} \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x = {x^4}\end{array} \right.\) \(\displaystyle \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x\left( {{x^3} - 1} \right) = 0\end{array} \right.\) \(\displaystyle \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)

Khi đó

\(\displaystyle {S_1} = \int\limits_0^1 {\left| {\sqrt x - {x^2}} \right|dx} \) \(\displaystyle = \left| {\int\limits_0^1 {\left( {\sqrt x - {x^2}} \right)dx} } \right|\) \(\displaystyle = \left| {\left. {\left( {\frac{2}{3}{x^{\frac{3}{2}}} - \frac{{{x^3}}}{3}} \right)} \right|_0^1} \right| = \left| {\frac{2}{3} - \frac{1}{3}} \right| = \frac{1}{3}\)

\(\displaystyle \sqrt {1 - {x^2}} = 1 - x\) \(\displaystyle \Leftrightarrow \left\{ \begin{array}{l}1 - x \ge 0\\1 - {x^2} = {\left( {1 - x} \right)^2}\end{array} \right.\) \(\displaystyle \Leftrightarrow \left\{ \begin{array}{l}x \le 1\\1 - {x^2} = 1 - 2x + {x^2}\end{array} \right.\)

\(\displaystyle \Leftrightarrow \left\{ \begin{array}{l}x \le 1\\2{x^2} - 2x = 0\end{array} \right.\) \(\displaystyle \Leftrightarrow \left\{ \begin{array}{l}x \le 1\\\left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)

Khi đó

\(\displaystyle {S_2} = \int\limits_0^1 {\left| {\sqrt {1 - {x^2}} - \left( {1 - x} \right)} \right|dx} \) \(\displaystyle = \int\limits_0^1 {\left| {\sqrt {1 - {x^2}} - 1 + x} \right|dx} \) \(\displaystyle = \left| {\int\limits_0^1 {\left( {\sqrt {1 - {x^2}} - 1 + x} \right)dx} } \right|\)

\(\displaystyle = \left| {\int\limits_0^1 {\sqrt {1 - {x^2}} dx} - \int\limits_0^1 {dx} + \int\limits_0^1 {xdx} } \right|\) \(\displaystyle = \left| {\int\limits_0^1 {\sqrt {1 - {x^2}} dx} - 1 + \frac{1}{2}} \right|\) \(\displaystyle = \left| {I - \frac{1}{2}} \right|\)

Tính \(\displaystyle I = \int\limits_0^1 {\sqrt {1 - {x^2}} dx}\)

Đặt

\(\displaystyle x = \sin t \Rightarrow dx = \cos tdt\) \(\displaystyle \Rightarrow I = \int\limits_0^{\frac{\pi }{2}} {\sqrt {1 - {{\sin }^2}t} .\cos tdt} \) \(\displaystyle = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^2}tdt}\)

\(\displaystyle = \frac{1}{2}\int\limits_0^{\frac{\pi }{2}} {\left( {1 + \cos 2t} \right)dt} \) \(\displaystyle = \frac{1}{2}\left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_0^{\frac{\pi }{2}}\) \(\displaystyle = \frac{1}{2}.\frac{\pi }{2} = \frac{\pi }{4}\)

Do đó \(\displaystyle {S_1} \ne {S_2}\)

Cho hình phẳng R giới hạn bởi các đường sau đây: \(y_1=f_1(x), y_2=f_2(x)\,,\,\,(f_1,f_2\)là các hàm liên tục trên đoạn [a;b]), x = a và x = b. Hãy chỉ ra công thức sai trong việc tính diện tích hình R.

A. \(\int\limits_{a}^{b}{\left| f_1\left( x \right)-f_2\left( x \right) \right|dx} \)

B. \(\int\limits_{a}^{b}{\left| f_2\left( x \right)-f_1\left( x \right) \right|dx} \)

C. \(\left| \int\limits_{b}^{a}{|f_1\left( x \right)-f_2\left( x \right)| dx} \right|\)

D. \(\left| \int\limits_{a}^{b}{[f_1\left( x \right)-f_2\left( x \right) ]dx} \right|\)

Phương pháp giải

Sử dụng công thức tính diện tích \(\displaystyle S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)

Hướng dẫn giải

Dễ thấy các đáp án A, B, C đều đúng.

Đáp án D chưa chắc đúng.

Chọn D.

Diện tích hình phẳng P giới hạn bởi các đường: \(y_1=x, y_2=2x, y_3=2-x\) bằng:

A. 1

B. \(\dfrac{2}{3}\)

C. 2

D. \(\dfrac{1}{3}\)

Phương pháp giải

sử dụng công thức \(\displaystyle S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx}\)

Hướng dẫn giải

Diện tích: 

\(\begin{aligned} & S=\int\limits_{0}^{\frac{2}{3}}{\left( 2x-x \right)dx+\int\limits_{\frac{2}{3}}^{1}{\left( 2-x-x \right)dx}} \\ & \,\,\,\,=\frac{{{x}^{2}}}{2}\left| \begin{aligned} & \frac{2}{3} \\ & 0 \\ \end{aligned} \right.+\left( 2x-{{x}^{2}} \right)\left| \begin{aligned} & 1 \\ & \frac{2}{3} \\ \end{aligned} \right. \\ & \,\,\,\,=\frac{1}{3} \\ \end{aligned} \)

Chọn D

Diện tích của hình phẳng được giới hạn bởi các đường : \(y_1=x^3, y_2=4x\) bằng:

A. 0

B. 4

C. 8

D. -8

Phương pháp giải

- Giải phương trình hoành độ giao điểm tìm nghiệm.

- Tính diện tích theo công thức \(\displaystyle  S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).

Hướng dẫn giải

Ta có:

\(\displaystyle {x^3} = 4x \Leftrightarrow x\left( {{x^2} - 4} \right) = 0\) \(\displaystyle \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\\x = 2\end{array} \right.\)

\(\displaystyle S = \int\limits_{ - 2}^2 {\left| {{x^3} - 4x} \right|dx} \) \(\displaystyle = \int\limits_{ - 2}^0 {\left| {{x^3} - 4x} \right|dx} + \int\limits_0^2 {\left| {{x^3} - 4x} \right|dx} \) \(\displaystyle = \int\limits_{ - 2}^0 {\left( {{x^3} - 4x} \right)dx} - \int\limits_0^2 {\left( {{x^3} - 4x} \right)dx}\)

\(\displaystyle = \left. {\left( {\frac{{{x^4}}}{4} - 2{x^2}} \right)} \right|_{ - 2}^0 - \left. {\left( {\frac{{{x^4}}}{4} - 2{x^2}} \right)} \right|_0^2\) \(\displaystyle = 0 - \frac{{16}}{4} + 2.4 - \frac{{16}}{4} + 2.4 = 8\)

Chọn C.

Cho hình phẳng H giới hạn bởi các đường : \(y=f(x), y=0, x=b, x=a\) (trong đó hàm số f(x) liên tục trên đoạn [b;a]. Thể tích khối tròn xoay tạo nên bởi phép quay hình H quanh trục Ox được cho bởi công thức:

A. \(\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\)

B. \(\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\)

C. \(\pi \int\limits_{b}^{a}{{{f}^{2}}\left( x \right)dx}\)

D. \(\pi \int\limits_{a}^{b}{[\pi f(x)]^2dx}\)

Phương pháp giải

Sử dụng công thức tính thể tích \(\displaystyle V = \pi \int\limits_u^v {{g^2}\left( x \right)dx}\)

Hướng dẫn giải

Thể tích tính theo công thức là \(\displaystyle V = \pi \int\limits_b^a {{f^2}\left( x \right)dx}\)

Chọn C.

Quay hình phẳng Q giới hạn bởi các đường: \(y_1=\sin x\) và \(y_2=\dfrac{2x}{\pi}\) quanh trục Ox, ta được một khối tròn xoay. Khi đó, thể tích của khối tròn xoay này bằng:

A. \(\dfrac{1}{6}\)

B. \(\dfrac{\pi}{6}\)

C. 8

D. \(\dfrac{\pi^2}{6}\)

Phương pháp giải

- Giải phương trình hoành độ tìm nghiệm.

- Tính thể tích theo công thức \(\displaystyle V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \)

Hướng dẫn giải

Ta có: \(\displaystyle \sin x = \frac{{2x}}{\pi } \Rightarrow \left[ \begin{array}{l}x = 0\\x = \frac{\pi }{2}\\x = - \frac{\pi }{2}\end{array} \right.\)

Khi đó \(\displaystyle V = \pi \int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\left| {{{\sin }^2}x - {{\left( {\frac{{2x}}{\pi }} \right)}^2}} \right|dx} \)

Dễ thấy \(\displaystyle f\left( x \right) = \left| {{{\sin }^2}x - {{\left( {\frac{{2x}}{\pi }} \right)}^2}} \right|\) là hàm số chẵn nên:

\(\displaystyle V = 2\pi \int\limits_0^{\frac{\pi }{2}} {\left| {{{\sin }^2}x - {{\left( {\frac{{2x}}{\pi }} \right)}^2}} \right|dx} \)\(\displaystyle = 2\pi \int\limits_0^{\frac{\pi }{2}} {\left( {{{\sin }^2}x - {{\left( {\frac{{2x}}{\pi }} \right)}^2}} \right)dx} \) \(\displaystyle = 2\pi \int\limits_0^{\frac{\pi }{2}} {{{\sin }^2}xdx} - \frac{8}{\pi }\int\limits_0^{\frac{\pi }{2}} {{x^2}dx} \)

\(\displaystyle = \pi \int\limits_0^{\frac{\pi }{2}} {\left( {1 - \cos 2x} \right)dx} - \frac{8}{\pi }\int\limits_0^{\frac{\pi }{2}} {{x^2}dx} \) \(\displaystyle = \pi \left. {\left( {x - \frac{{\sin 2x}}{2}} \right)} \right|_0^{\frac{\pi }{2}} - \frac{8}{\pi }.\left. {\frac{{{x^3}}}{3}} \right|_0^{\frac{\pi }{2}}\) \(\displaystyle = \pi \left( {\frac{\pi }{2} - 0} \right) - \frac{8}{\pi }.\frac{1}{3}.{\left( {\frac{\pi }{2}} \right)^3}\)

\(\displaystyle = \frac{{{\pi ^2}}}{2} - \frac{{{\pi ^2}}}{3} = \frac{{{\pi ^2}}}{6}\)

Chọn D.

Quay hình G giới hạn bởi các đường : \(y=x^3, y=1, x=0\) xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng

A. \(\pi\)

B. \(\dfrac{5}{3}\pi\)

C. \(\dfrac{3}{5}\pi\)

D. \(\dfrac{3}{5}\)

Phương pháp giải

- Rút x theo y

- Sử dụng công thức \(\displaystyle V = \pi \int\limits_a^b {{f^2}\left( y \right)dy} \)

Hướng dẫn giải

Ta có: \(\displaystyle y = {x^3} \Rightarrow x = \sqrt[3]{y}. \,\,Cho \,\, \displaystyle \sqrt[3]{y} = 0 \Leftrightarrow y = 0\)

Khi đó \(\displaystyle V = \pi \int\limits_0^1 {{{\left( {\sqrt[3]{y}} \right)}^2}dy} \) \(\displaystyle = \pi \int\limits_0^1 {{y^{\frac{2}{3}}}dy} \) \(\displaystyle = \pi \left. {\left( {\frac{3}{5}{y^{\frac{5}{3}}}} \right)} \right|_0^1 = \frac{3}{5}\pi\)

Chọn C.