Giải bài tập SBT Toán 12 Bài 4: Hàm số mũ. Hàm số lôgarit
Mời quý thầy cô giáo và các em học sinh cùng tham khảo nội dung giải bài tập bài Hàm số mũ và hàm số lôgarit SBT trang 117, 118, 119 Toán 8 dưới đây. Tài liệu gồm 19 bài tập có hướng dẫn giải và đáp án chi tiết sẽ giúp các em vừa ôn tập kiến thức vừa nâng cao kĩ năng giải bài tập đồng thời có kế hoạch học tập cụ thể. Chúc các em học tập thật tốt!
Mục lục nội dung
1. Giải bài 2.27 trang 117 SBT Giải tích 12
2. Giải bài 2.28 trang 117 SBT Giải tích 12
3. Giải bài 2.29 trang 117 SBT Giải tích 12
4. Giải bài 2.30 trang 117 SBT Giải tích 12
5. Giải bài 2.31 trang 117 SBT Giải tích 12
6. Giải bài 2.32 trang 117 SBT Giải tích 12
7. Giải bài 2.33 trang 117 SBT Giải tích 12
8. Giải bài 2.34 trang 118 SBT Giải tích 12
9. Giải bài 2.35 trang 118 SBT Giải tích 12
10. Giải bài 2.36 trang 118 SBT Giải tích 12
11. Giải bài 2.37 trang 118 SBT Giải tích 12
12. Giải bài 2.38 trang 118 SBT Giải tích 12
13. Giải bài 2.39 trang 108 SBT Giải tích 12
14. Giải bài 2.40 trang 108 SBT Giải tích 12
15. Giải bài 2.41 trang 118 SBT Giải tích 12
16. Giải bài 2.42 trang 119 SBT Giải tích 12
17. Giải bài 2.43 trang 119 SBT Giải tích 12

1. Giải bài 2.27 trang 117 SBT Giải tích 12
Hãy so sánh mỗi số sau với 1:
\(a)\,(0,1)^\sqrt 2;\\ b)\,(3,5)^{0,1}\\ c)\,\pi^{-2,7}\\ d) \left(\dfrac{\sqrt 5} 5 \right)^{-1,2}\)
Phương pháp giải
Sử dụng tính biến thiên của hàm số mũ: \(y=a^x\)
Khi \(a>1\) hàm số luôn đồng biến
Khi \(0< a< 1\) hàm số luôn nghịch biến
Hướng dẫn giải
a) \(0<0,1<1\Rightarrow (0,1)^{\sqrt 2}<1\)
b) \(3,5> 1\Rightarrow 3,5^{0,1}>1\)
c) \(\pi> 1\Rightarrow \dfrac 1 \pi < 1\Rightarrow \pi^{-2,7}=\left(\dfrac 1 \pi\right)^{2,7}<1\)
d) \(\left(\dfrac {\sqrt 5} 5 \right)^{-1,2}=\left(\dfrac 5 {\sqrt 5}\right)^{1,2}=(\sqrt 5) ^{1,2}>1\)
2. Giải bài 2.28 trang 117 SBT Giải tích 12
Tìm tọa độ giao điểm của đồ thị của mỗi cặp hàm số sau
a) \(y=2^x\) và \(y=8\)
b) \(y=3^x\) và \(y=\dfrac 1 3\)
c) \(y={{\left( \dfrac{1}{4} \right)}^{x}} \) và \(y=\dfrac 1 {16}\)
Phương pháp giải
Xét phương trình hoành độ giao điểm
\(a^x=a^y\Rightarrow x=y\)
Hướng dẫn giải
a)
\(2^x=8=2^3\Rightarrow x=3\)
Tọa độ giao điểm \((3;8)\)
b)
\(3^x=\dfrac 1 3=3^{-1}\Rightarrow x=-1\)
Tọa độ giao điểm \(\left(-1;\dfrac 1 3\right)\)
c)
\(\left(\dfrac 1 4\right)^x=\dfrac{1} {16}=\left(\dfrac 1 4\right)^2\Rightarrow x=2\)
Tọa độ giao điểm \(\left(2;\dfrac 1 {16}\right)\)
d)
\(\left(\dfrac 1 3\right)^x=9\Rightarrow3^{-x}=3^2\Rightarrow x=-2\)
Tọa độ giao điểm \((-2;9)\)
3. Giải bài 2.29 trang 117 SBT Giải tích 12
Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau :
a) \((1,7)^3\) và 1
b) \((0,3)^2\) và 1
c) \((3,2)^{1,5}\) và \((3,2)^{1,6}\)
d) \((0,2)^{-3}\) và \((0,2)^{-2}\)
e) \({{\left( \dfrac{1}{5} \right)}^{\sqrt{2}}}\) và \({{\left( \dfrac{1}{5} \right)}^{1,4}} \)
f) \({{6}^{\pi }}\) và \({{6}^{3,14}} \)
Phương pháp giải
Tính đồng biến và nghịch biến của hàm số mũ: \(y=a^x \)
Khi \(a> 1\) hàm số luôn đồng biến
Khi \(0< a< 1\) hàm số luôn nghịch biến
Tức là:
Khi \(a > 1\) thì với \(0< x_1< x_2 \Rightarrow a^{x_1}< x^{x_2}\)
Khi \(0< a< 1\) thì với \(0< x_1< x_2 \Rightarrow a^{x_1}>x^{x_2}\)
Hướng dẫn giải
a)
Vì \(1,7>1\Rightarrow (1,7)^3>1\)
b)
Vì \(0,3 < 1\Rightarrow (0,3)^2<1\)
c)
Vì \(3,2>1\Rightarrow (3,2)^{1,5}<(3,2)^{1,6}\)
d)
\((0,2)^{-3}=5^3;\,\,\,(0,2)^{-2}=5^2\Rightarrow (0,2)^{-3}>(0,2)^{-2}\)
e)
Vì \(\dfrac 1 5 < 1;\,\,\sqrt 2 > 1,4\Rightarrow \left(\dfrac 1 5 \right)^{\sqrt 2} < \left(\dfrac 1 5 \right)^{1,4}\)
f)
\(\pi>3,14\Rightarrow 6^\pi>6^{3,14}\)
4. Giải bài 2.30 trang 117 SBT Giải tích 12
Từ đồ thị hàm số \(y=3^x\), hãy vẽ đồ thị các hàm số sau:
a) \(y=3^x-2\)
b) \( y=3^x+2\)
c) \(y=|3^x-2| \)
d) \(y=2-3^x\)
Phương pháp giải
a), b) Tịnh tiến đồ thị hàm số \(y = {3^x}\) lên trên hoặc xuống dưới 2 đơn vị.
c) Đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có được từ đồ thị hàm số y = f( x ) bằng cách:
+ Giữ nghuyên phần đồ thị hàm số y = f( x ) phía trên trục hoành.
+ Lấy đối xứng phần dưới qua trục hoành và xóa phần dưới cũ đi.
c) Đồ thị hàm số y = - f( x ) có được từ đồ thị hàm số y = f( x ) bằng cách lấy đối xứng toàn bộ đồ thị hàm số y=f(x) qua trục hoành.
Hướng dẫn giải
a)
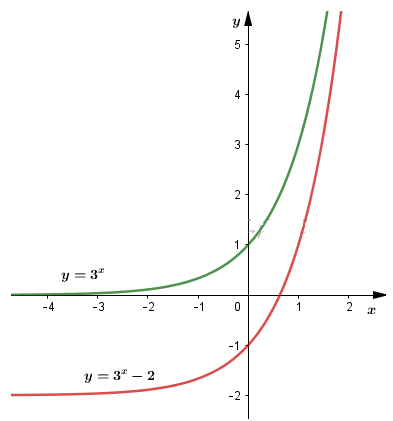
\(y=3^x-2=f(x)-2\)
Đồ thị hàm số \(y=3^x-2\) nhận được từ đồ thị hàm số \(f(x)\) bằng phép tịnh tiến song song với trục Oy xuống dưới 2 đơn vị.
b)
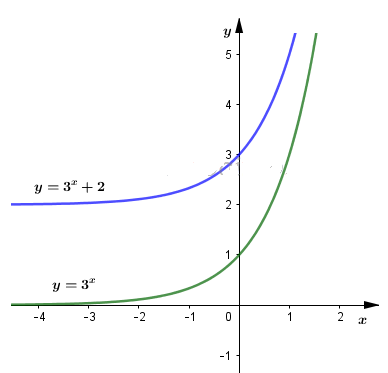
\(y=3^x+2=f(x)+2\)
Đồ thị hàm số \(y=3^x+2\) nhận được từ đồ thị hàm số \(f(x)\) bằng phép tịnh tiến song song với trục Oy lên trên 2 đơn vị.
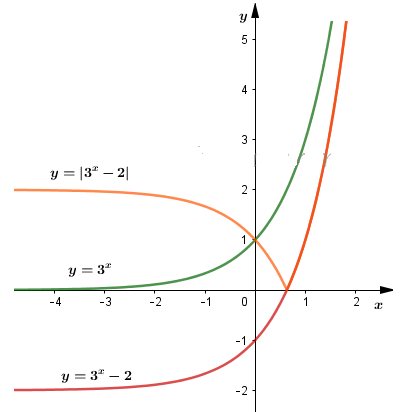
c)\(y=|3^x-2|=\left\{\begin{align}&3^x-2\,\,\text{khi}\,\,3^x-2>0\\ &2-3^x\,\,\,\text{khi}\,\,\,3^x-2<0\\ \end{align}\right.\)
Do vậy đồ thị hàm số \(y=|3^x-2|\) gồm hai phần:
- Giữa nguyên phần đồ thị hàm số \(y=3^x-2\) nằm phía trên trục hoành.
- Phần đồ thị hàm số \(y=3^x-2\) nằm phía dưới trục hoành, ta lấy đối xứng qua trục hoành.
d)
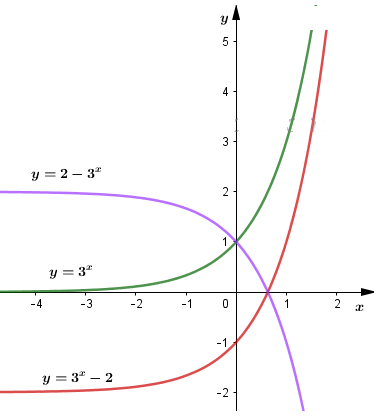
\(y=2-3^x=-(3^x-2)\)
Ta có đồ thị của hàm số \(y =2-3^x\) đối xứng với đồ thị của hàm số \(y=3^x\) qua trục hoành
5. Giải bài 2.31 trang 117 SBT Giải tích 12
Tìm giá trị lớn nhất, nhỏ nhất của hàm số \(y=2^{|x|}\) trên đoạn \([-1;1]\)
Phương pháp giải
- Viết hàm số \(y = {2^{\left| x \right|}}\) dưới dạng khoảng.
- Xét từng hàm số có được trên các khoảng thích hợp.
- Tìm GTLN, GTNN và kết luận.
Hướng dẫn giải
Ta có
\({{2}^{|x|}}=\left\{ \begin{align} & {{2}^{-x}}\,\,\,\,\,\,\text{khi}\,\,\,\,\,x\,\in [-1;0]\\ & {{2}^{x}}\,\,\,\,\,\,\,\,\,\text{khi}\,\,\,\,x\in [0;1] \\ \end{align} \right. \)
Trên đoạn \([-1;0]\), hàm số nghịch biến nên hàm số đạt giá trị lớn nhất là \({{2}^{-\left( -1 \right)}}={{2}^{1}}=2 \), hàm số đạt giá trị nhỏ nhất là \({{2}^{0}}=1 \)
Trên đoạn \([0;1]\), hàm số đồng biến nên hàm số đạt giá trị lớn nhất là \({{2}^{1}}=2\), hàm số đạt giá trị nhỏ nhất là \({{2}^{0}}=1 \)
Vậy \(\underset{[-1;1]}{\mathop{Max}}\,y=2;\,\underset{[-1;1]}{\mathop{Min}}\,y=1 \)
6. Giải bài 2.32 trang 117 SBT Giải tích 12
Tìm tập xác định của các hàm số sau:
\(\begin{align} & a)y={{\log }_{8}}\left( {{x}^{2}}-3x-4 \right) \\ & b)y={{\log }_{\sqrt{3}}}\left( -{{x}^{2}}+5x+6 \right) \\ & c)y={{\log }_{0,7}}\dfrac{{{x}^{2}}-9}{x+5} \\ & d)y={{\log }_{\frac{1}{3}}}\dfrac{x-4}{x+4} \\ & e)y={{\log }_{\pi }}\left( {{2}^{x}}-2 \right) \\ & f)y={{\log }_{3}}\left( {{3}^{x-1}}-9 \right) \\ \end{align} \)
Phương pháp giải
Hàm số \(y=\log_ax\) có tập xác định là \((0;+\infty)\)
Hướng dẫn giải
a)
\({{x}^{2}}-3x-4>0\Leftrightarrow \left( x+1 \right)(x-4)>0\Leftrightarrow x\in \left( -\infty ;-1 \right)\cup \left( 4;+\infty \right) \)
b)
\(-{{x}^{2}}+5x+6>0\Leftrightarrow \left( -x-1 \right)\left( x-6 \right)>0\Leftrightarrow x\in \left( -1;6 \right) \)
c)
\(\dfrac{{{x}^{2}}-9}{x+5}>0\Leftrightarrow \dfrac{\left( x-3 \right)\left( x+3 \right)}{x+5}>0 \)
Bảng xét dấu:
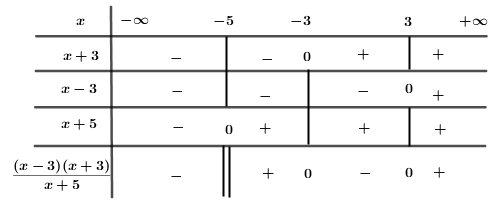
Vậy \(x\in \left( -5;-3 \right)\cup \left( 3;+\infty \right) \)
d)
\(\dfrac{x-4}{x+4}>0\Leftrightarrow x\in \left( -\infty ;-4 \right)\cup \left( 4;+\infty \right) \)
e)
\({{2}^{x}}-2>0\Leftrightarrow {{2}^{x}}>{{2}^{1}}\Leftrightarrow x>1 \)
f)
\({{3}^{x-1}}-9>0\Leftrightarrow {{3}^{x-1}}>{{3}^{2}}\Leftrightarrow x-1>2\Leftrightarrow x>3\Leftrightarrow x\in \left( 3;+\infty \right) \)
7. Giải bài 2.33 trang 117 SBT Giải tích 12
Tính đạo hàm của các hàm số cho ở bài tập 2.32
\(\begin{align} & a)y={{\log }_{8}}\left( {{x}^{2}}-3x-4 \right) \\ & b)y={{\log }_{\sqrt{3}}}\left( -{{x}^{2}}+5x+6 \right) \\ & c)y={{\log }_{0,7}}\dfrac{{{x}^{2}}-9}{x+5} \\ & d)y={{\log }_{\frac{1}{3}}}\dfrac{x-4}{x+4} \\ & e)y={{\log }_{\pi }}\left( {{2}^{x}}-2 \right) \\ & f)y={{\log }_{3}}\left( {{3}^{x-1}}-9 \right) \\ \end{align} \)
Phương pháp giải
Áp dụng: Đạo hàm của hàm số lôgarit tính bởi:
\(\left(\log_au\right)'=\dfrac{u'}{u\ln a}\)
Hướng dẫn giải
a)
\(\left[ {{\log }_{8}}\left( {{x}^{2}}-3x-4 \right) \right]'=\dfrac{2x-3}{\left( {{x}^{2}}-3x-4 \right)\ln 8} \)
b)
\(\left[ {{\log }_{\sqrt{3}}}\left( -{{x}^{2}}+5x+6 \right) \right]'=\dfrac{-2x+5}{\left( -{{x}^{2}}+5x+6 \right)\ln \sqrt{3}} \)
c)
\(\left( {{\log }_{0,7}}\dfrac{{{x}^{2}}-9}{x+5} \right)'=\dfrac{\dfrac{2x\left( x+5 \right)-\left( {{x}^{2}}-9 \right)}{{{\left( x+5 \right)}^{2}}}}{\left( \dfrac{{{x}^{2}}-9}{x+5} \right)\ln \left( 0,7 \right)}=\dfrac{{{x}^{2}}+10x+9}{\left( x+5 \right)\left( {{x}^{2}}-9 \right)\ln \left( 0,7 \right)} \)
d)
\(\left( {{\log }_{\frac{1}{3}}}\dfrac{x-4}{x+4} \right)'=\dfrac{\dfrac{8}{{{\left( x+4 \right)}^{2}}}}{\dfrac{x-4}{x+4}\ln \dfrac{1}{3}}=\dfrac{8}{\left( {{x}^{2}}-16 \right)\ln 3} \)
e)
\(\left[ {{\log }_{\pi }}\left( {{2}^{x}}-2 \right) \right]'=\dfrac{{{2}^{x}}\ln 2}{\left( {{2}^{x}}-2 \right)\ln \pi } \)
f)
\(\left[ {{\log }_{3}}\left( {{3}^{x-1}}-9 \right) \right]'=\dfrac{{{3}^{x-1}}\ln 3}{\left( {{3}^{x-1}}-9 \right)\ln 3}=\dfrac{{{3}^{x-1}}}{{{3}^{x-1}}-9} \)
8. Giải bài 2.34 trang 118 SBT Giải tích 12
Hãy so sánh \(x\) với 1 biết:
a) \(\log_3x=-0,3\)
b) \(\log_{\frac 1 3}x=1,7\)
c) \(\log_2x=1,3\)
d) \(\log_{\frac 1 4}x=-1,1\)
Phương pháp giải
Tìm x và so sánh, sử dụng tính chất so sánh mũ.
Hướng dẫn giải
a)
\(\log_3x=-0,3<\log_31\Rightarrow x < 1\)
b)
\(\log_{\frac 1 3}x=1,7\Rightarrow \log_3 x=-1,7<\log_31\Rightarrow x< 1\)
c)
\(\log_2x=1,3>\log_21\Rightarrow x > 1\)
d)
\(\log_{\frac 1 4}x=-1,1\Rightarrow \log_4x=1,1>\log_41\Rightarrow x > 1\)
9. Giải bài 2.35 trang 118 SBT Giải tích 12
Trong các hàm số sau, hàm số nào đồng?
A. \(y=\left(\dfrac{\sqrt 3} 2\right)^x\)
B. \(y=\left(\dfrac{e} 3\right)^x\)
C. \(y=\left(\dfrac{\pi} 4\right)^x\)
D. \(y=\left(\dfrac{3} e\right)^x\)
Phương pháp giải
Hàm số \(y=a^x\) đồng biến khi a > 1 ; nghịch biến khi 0 < a < 1
Hướng dẫn giải
Ta có:
\(\dfrac {\sqrt 3 }2<\dfrac{\sqrt 4} 2 =1;\\ \dfrac e 3 < 1;\\ \dfrac {\pi} 4< 1;\\ \dfrac 3 e > 1.\)
Vậy hàm số \(y=\left(\dfrac{3} e\right)^x\) đồng biến.
Chọn D.
10. Giải bài 2.36 trang 118 SBT Giải tích 12
Trong các hàm số sau, hàm số nào nghịch biến?
A. \(y=\left(\dfrac2{\sqrt 3}\right)^x\)
B. \(y=\left(\dfrac3{\pi}\right)^x\)
C. \(y=\pi^x\)
D. \(y=\left(\dfrac{\sqrt 5}2\right)^x\)
Phương pháp giải
Hàm số \(y=a^x\) đồng biến khi a > 1 ; nghịch biến khi 0 < a < 1
Hướng dẫn giải
Ta có:
\(\dfrac 2 {\sqrt 3}>1;\\ \dfrac{3}{\pi}<1;\\ \pi > 1;\\ \dfrac{\sqrt 5} 2 > 1.\)
Hàm số \(y=\left(\dfrac3{\pi}\right)^x\) nghịch biến.
Chọn B
11. Giải bài 2.37 trang 118 SBT Giải tích 12
Với giá trị nào của \(x\) thì đồ thị hàm số \(y=4^x\) nằm phía trên đường thẳng \(y=1\)?
A. \(x> 0\)
B. \(x< 0\)
C. \(x=0\)
D. \(x< 1\)
Phương pháp giải
Đồ thị hàm số y = f(x) nằm phía trên đường thẳng y = 1 khi f(x) > 1
Hướng dẫn giải
Ta có:
\(4^x>1\Rightarrow x > 0\)
Chọn A.
12. Giải bài 2.38 trang 118 SBT Giải tích 12
Với giá trị nào của x thì đồ thị hàm số \( y=\left(\dfrac 2 3 \right)^x\) mằm phía trên đường thẳng \(y=1\)?
A. \(x> 0\)
B. \(x< 0\)
C. \(x=0\)
D. \(x< 1\)
Phương pháp giải
Đồ thị hàm số y = f(x) nằm phía trên đường thẳng y = 1 khi f(x) > 1
Hướng dẫn giải
\(\left(\dfrac 2 3 \right)^x > 1\Rightarrow x < 0\)
Chọn B.
13. Giải bài 2.39 trang 108 SBT Giải tích 12
Tìm \(x ,\) biết \(2^x=64\)
A. \(x=4\)
B. \(x=5\)
C. \(x=6\)
D. \(x=8\)
Phương pháp giải
Sử dụng lý thuyết \(\displaystyle {a^m} = {a^n} \Leftrightarrow m = n\)
Hướng dẫn giải
\(2^x=4=2^6\\ \Rightarrow x=6\)
Chọn C.
14. Giải bài 2.40 trang 108 SBT Giải tích 12
Tìm \(x ,\) biết \(3^x=\dfrac 1 {81}\)
A. \(x=4\)
B. \(x=-4\)
C. \(x=3\)
D. \(x=-3\)
Phương pháp giải
Sử dụng lý thuyết \(\displaystyle {a^m} = {a^n} \Leftrightarrow m = n\)
Hướng dẫn giải
\(3^x=\dfrac 1 {81}=3^{-4}\\ \Rightarrow x =-4\)
Chọn B.
15. Giải bài 2.41 trang 118 SBT Giải tích 12
Tìm \(x ,\) biết \( \left(\dfrac 1 4\right) ^x=16\)
A. \(x=-2\)
B. \(x=2\)
C. \(x=\dfrac 1 2\)
D. \(x=-\dfrac 1 2\)
Phương pháp giải
Sử dụng lý thuyết \(\displaystyle {a^m} = {a^n} \Leftrightarrow m = n\)
Hướng dẫn giải
\(\left(\dfrac 1 4\right)^x=16\\ \Rightarrow 2^{-2x}=2^4\\ \Rightarrow x=-2\)
Chọn A
16. Giải bài 2.42 trang 119 SBT Giải tích 12
Tìm x, biết \(9^x=\dfrac 1 3\)
A. \(x=-2\)
B. \(x=2\)
C. \(x=\dfrac 1 2\)
D. \(x=-\dfrac 1 2\)
Phương pháp giải
Sử dụng lý thuyết \(\displaystyle {a^m} = {a^n} \Leftrightarrow m = n\)
Hướng dẫn giải
\(9^x=\dfrac 1 3\\ \Rightarrow 3^{2x}=3^{-1}\\ \Rightarrow x=-\dfrac 1 2\)
Chọn D.
17. Giải bài 2.43 trang 119 SBT Giải tích 12
Tìm x, biết \((\sqrt 3 -\sqrt 2)^x=\sqrt 3 +\sqrt 2\)
A. \(x=1\)
B. \( x=2\)
C. \(x=\dfrac 1 2\)
D. \(x=-1\)
Phương pháp giải
Sử dụng lý thuyết \(\displaystyle {a^m} = {a^n} \Leftrightarrow m = n\)
Hướng dẫn giải
\((\sqrt 3 -\sqrt 2)^x=\sqrt 3 +\sqrt 2\\ \Rightarrow (\sqrt 3 -\sqrt 2 )^x=\dfrac{(\sqrt 3 +\sqrt 2)(\sqrt 3 -\sqrt 2)}{\sqrt 3 -\sqrt 2}\\ \Rightarrow (\sqrt 3 -\sqrt 2)^x=\dfrac 1 {\sqrt 3 -\sqrt 2}\\ \Rightarrow x=-1\)
Chọn D.
18. Giải bài 2.44 trang 119 SBT Giải tích 12
Trong các hàm số sau đây, hàm số nào đồng biến?
A. \(y=\log_{\frac 1 e}x\)
B. \(y=\log_{\frac{\pi} 3} x\)
C. \(y=\log_{\frac{\sqrt 2} 2}x\)
D. \(y=\log_{\frac e 3}x\)
Phương pháp giải
Hàm số \(y=\log_ax\) đồng biến khi a > 1, nghịch biến khi 0 < a < 1
Hướng dẫn giải
Ta thấy \(\displaystyle \frac {\pi }{3} > 1\) nên hàm số \(\displaystyle y = {\log _{\frac {\pi }{3}}}x\) đồng biến trên \(\displaystyle \left( {0; + \infty } \right)\)
Chọn B.
19. Giải bài 2.45 trang 119 SBT Giải tích 12
Trong các hàm số sau đây, hàm số nào nghịch biến?
A. \(y=\lg x\)
B. \( y=\ln x\)
C. \(y=\log_{\sqrt 3} x\)
D. \(y=\log_{\frac 2 e}x\)
Phương pháp giải
Hàm số \(y=\log_ax\) đồng biến khi a > 1, nghịch biến khi
Hướng dẫn giải
Ta thấy \(\displaystyle 0 < \frac {2}{e} < 1\) nên hàm số \(\displaystyle y = {\log _{\frac {2}{e}}}x\) nghịch biến trên \(\displaystyle \left( {0; + \infty } \right)\)
Chọn D.
Các em hãy luyện tập bài trắc nghiệm Hàm số mũ. Hàm số lôgarit Toán 12 sau để nắm rõ thêm kiến thức bài học.
Tham khảo thêm
- doc Giải bài tập SBT Toán 12 Bài 1: Lũy thừa
- doc Giải bài tập SBT Toán 12 Bài 2: Hàm số lũy thừa
- doc Giải bài tập SBT Toán 12 Bài 3: Lôgarit
- doc Giải bài tập SBT Toán 12 Bài 5: Phương trình mũ và phương trình lôgarit
- doc Giải bài tập SBT Toán 12 Bài 6: Bất phương trình mũ và bất phương trình lôgarit



