Giải bài tập SBT Toán 12 Bài 2: Hàm số lũy thừa
Mời các em học sinh lớp 12 cùng tham khảo nội dung giải bài tập SBT bài Trường hợp đồng dạng thứ hai trang 104 dưới đây. Bài gồm có 9 bài tập được eLib sưu tầm và tổng hợp. Với nội dung chi tiết, rõ ràng giúp các em ôn tập lại các kiến thức đã học và vận dụng vào giải các bài tập tương tự. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy của quý thầy cô và học tập của các em học sinh.
Mục lục nội dung
1. Giải bài 2.6 trang 104 SBT Giải tích 12
2. Giải bài 2.7 trang 104 SBT Giải tích 12
3. Giải bài 2.8 trang 104 SBT Giải tích 12
4. Giải bài 2.9 trang 104 SBT Giải tích 12
5. Giải bài 2.10 trang 104 SBT Giải tích 12
6. Giải bài 2.11 trang 104 SBT Giải tích 12
7. Giải bài 2.12 trang 104 SBT Giải tích 12

1. Giải bài 2.6 trang 104 SBT Giải tích 12
Tìm tập xác định của các hàm số sau:
a) \(y=(x^2-4x+3)^{-2}\)
b) \(y=(x^3-8)^{\frac{\pi} 3}\)
c) \(y=(x^3-3x^2+2x)^{\frac 1 4}\)
d) \(y=(x^2+x-6)^{-\frac 1 3}\)
Phương pháp giải
Sử dụng lý thuyết về tập xác định của hàm số lũy thừa.
+ Lũy thừa có số mũ nguyên dương thì cơ số tùy ý.
+ Lũy thừa có số mũ nguyên âm hoặc bằng 0 thì cơ số khác 0.
+ Lũy thừa có số mũ không nguyên thì cơ số phải dương.
Hướng dẫn giải
a) ĐKXĐ:
\(x^2-4x+3\ne 0\Leftrightarrow x\notin \{1;3\}\)
TXĐ: \(\mathbb{R}\backslash \left\{ 1;3 \right\}\)
b) ĐKXĐ: \(x^3-8>0\Rightarrow x^3>8\Leftrightarrow x > 2\)
TXĐ: \((2;+\infty)\)
c) ĐKXĐ: \(x^3-2x^2+2x>0\Rightarrow x(x^2-2x+2)>0\Rightarrow x > 0\)
(vì \(x^2-2x+2=(x-1)^2+1>0\,\,\forall x\in \mathbb R\))
TXĐ: \((0;+\infty)\)
d) ĐKXĐ: \(x^2+x-6>0\Rightarrow x\in (-\infty;-3)\cup (2;+\infty)\)
TXĐ: \((-\infty;-3)\cup (2;+\infty)\)
2. Giải bài 2.7 trang 104 SBT Giải tích 12
Tính đạo hàm của các hàm số cho ở bài tập 2.6
a) \(y=(x^2-4x+3)^{-2}\)
b) \(y=(x^3-8)^{\frac{\pi} 3}\)
c) \(y=(x^3-3x^2+2x)^{\frac 1 4}\)
d) \(y=(x^2+x-6)^{-\frac 1 3}\)
Phương pháp giải
Áp dụng: \((u^\alpha)'=\alpha.u'.u^{\alpha -1}\)
Hướng dẫn giải
a)
\(y'=-2(2x-4)(x^2-4x+3)^{-2-1}=-2(2x-4)(x^2-4x+3)^{-3}\)
b)
\(y'=\dfrac{\pi} 3 .3x^2.(x^3-8)^{\frac\pi 3-1}=\pi x^2(x^3-8)^{\frac{\pi-3}3}\)
c)
\(y'=\dfrac 1 4 (3x^2-6x+2).(x^3-3x^2+2x)^{\frac 1 4 -1}\\ =\dfrac 1 4(3x^2-6x+2).(x^3-3x^2+2x)^{-\frac 3 4}\)
d)
\(y'=-\dfrac 1 3(2x+1)(x^2+x-6)^{-\frac 1 3 -1}\\ =-\dfrac 1 3 (2x+1)(x^2+x-6)^{-\frac 4 3}\)
3. Giải bài 2.8 trang 104 SBT Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau :
a) \(y=x^{-3}\)
b) \(y=x^{-\frac 1 2}\)
c) \(y=x^{\frac {\pi} 4}\)
Phương pháp giải
Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:
- Tìm tập xác định
- Tính đạo hàm
- Tìm giới hạn xác định các tiệm cận (nếu có)
- Lập bảng biến thiên
- Vẽ đồ thị
Hướng dẫn giải
a)
\(y=x^{-3}=\dfrac1 {x^3}\)
TXĐ: \(D=\mathbb{R}\backslash \left\{ 0 \right\}\)
Hàm số đã cho là hàm lẻ vì \(y(x)=-y(-x)\)
\(y'=-3x^{-4}=-\dfrac 3 {x^4}<0\,\,\forall x\in D\)
\(\lim\limits_{x\to 0^-}y=-\infty; \lim\limits_{x\to 0^+}y=+\infty\\ \lim\limits_{x\to -\infty}y=\lim\limits_{x\to +\infty}y=0\)
Đồ thị có tiệm cận đứng là trục tung và tiệm cận ngang là trục hoành.
Bảng biến thiên
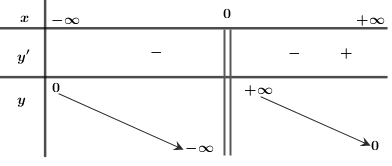
Đồ thị nhận gốc O là tâm đối xứng
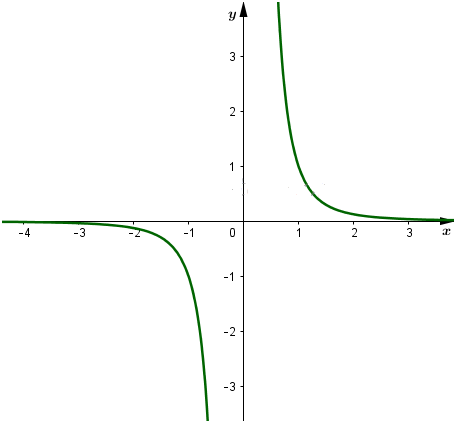
b)
\(y=x^{-\frac 1 2}=\dfrac1 {\sqrt x}\)
TXĐ: \(D=(0;+\infty)\)
\(y'=-\dfrac 1 2x^{-\frac 3 2}=-\dfrac 1 {2\sqrt{x^3}}<0\,\,\forall x\in D\)
\(\lim\limits_{x\to 0}y=+\infty\\ \lim\limits_{x\to +\infty}y=0\)
Đồ thị có tiệm cận đứng là trục tung và tiệm cận ngang là trục hoành.
Bảng biến thiên
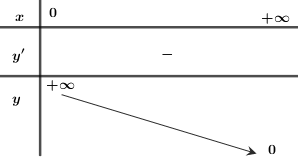
Đồ thị
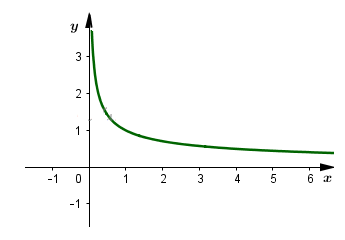
c)
\(y=x^{\frac \pi 4}\)
TXĐ: \(D=(0;+\infty)\)
\(y'=\dfrac {\pi} 4 x^{\frac \pi 4 -1} > 0\,\,\forall x\in D\)
\(\lim\limits_{x\to 0}y=0\\ \lim\limits_{x\to+\infty}y=+\infty\)
Đồ thị không có tiệm cận
Bảng biến thiên

Đồ thị
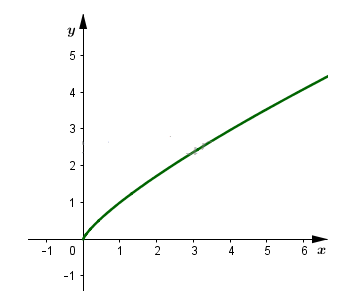
4. Giải bài 2.9 trang 104 SBT Giải tích 12
Vẽ đồ thị của các hàm số \(y=x^2\) và \(y=x^{\frac 1 2}\) trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi \(x=0,5;1;\dfrac 3 2; 2; 3; 4\)
Phương pháp giải
- Vẽ đồ thị các hàm số đã cho dựa vào kiến thức đã học về hàm số bậc hai và hàm số lũy thừa.
- So sánh giá trị của hai hàm số tại các điểm \(x = {x_i}\) bằng cách dựng đường thẳng \(x = {x_i}\) và nhận xét vị trí các điểm giao trên hình vẽ.
Hướng dẫn giải
+) Vẽ đồ thị hàm số \(y=x^{2}\)
TXĐ: \(D=\mathbb R\)
Hàm số là hàm chẵn vì \(y(x)=y(-x)\)
\(y'=2x\\ y'=0\Rightarrow x=0\)
\(\lim\limits_{x\to -\infty}y= \lim\limits_{x\to +\infty}y=+\infty\)
Đồ thị không có tiệm cận, nhận trục tung là trục đối xứng.
Bảng biến thiên
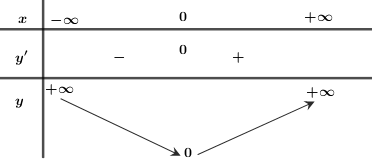
+) Vẽ đồ thị hàm số \(y=x^{\frac 12}\)
TXĐ: \(D=(0;+\infty)\)
\(y'=\dfrac 1 2 x^{-\frac 1 2}=\dfrac {1}{2\sqrt x}\)
\(\lim\limits_{x\to 0}y=0 \\ \lim\limits_{x\to +\infty}y=+\infty\)
Đồ thị không có tiệm cận
Bảng biến thiên
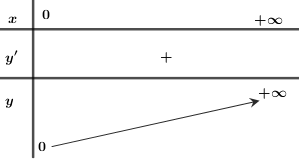
Đồ thị hai hàm số:
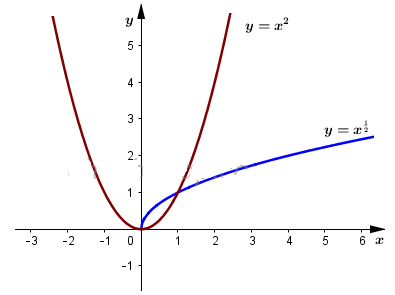
Đặt \(f(x)=x^2; g(x)=x^{\frac 1 2}\)
\(\bullet\)Tại \(x=0,5\):
\(f(0,5)=0,5^2; g(0,5)=0,5^{\frac 1 2}\)
Vì \(0<0,5<1\) và \(2>\dfrac 1 2\) nên \(f(0,5)< g(0,5)\)
\(\bullet\)Tại \(x=1\):
\(f(1)=1^2=1; g(1)=1^{\frac 1 2}=1\)
Nên \(f(1)= g(1)\)
\(\bullet\)Tại \(x=\dfrac 3 2\):
\(f\left(\dfrac 3 2\right)=\left(\dfrac 3 2\right)^2; g\left(\dfrac 3 2\right)=\left(\dfrac 3 2\right)^{\frac 1 2}\)
Vì \(\dfrac 3 2>1\) và \(2>\dfrac 1 2\) nên \(f\left(\dfrac 3 2\right)> g\left(\dfrac 3 2\right)\)
Từ đồ thị hàm số nhận thấy từ giá trị \( x= 1\) trở đi, hàm số \(y=f(x)\) luôn lớn hơn \(y=g(x\)). Hay
\(f(2)>g(2)\\ f(3)>g(3)\\ f(4)>g(4)\)
5. Giải bài 2.10 trang 104 SBT Giải tích 12
Tìm x, sao cho \(x^{-4}=16\).
A. \(x=2\)
B. \(x=-2\)
C. \(x=\dfrac 1 2\)
D. \(x=4\)
Phương pháp giải
Biến đổi phương trình về dạng \({x^n} = {a^n} \Leftrightarrow x = \pm a\) với n chẵn.
Hướng dẫn giải
Ta có:
\(x^{-4}=16\\ \Rightarrow \dfrac 1 {x^4}=\dfrac 1{16}\\ \Leftrightarrow x=\dfrac 1 2\)
Chọn C.
6. Giải bài 2.11 trang 104 SBT Giải tích 12
Tìm số lớn nhất trong các số: \(0,3^{\pi};0,3^{0,5}; 0,3^{\frac 2 3}; 0,3 ^{3,1415}\)
A. \( 0,3^{\pi}\)
B. \(0,3^{0,5}\)
C. \(0,3^{\frac 2 3}\)
D. \(0,3 ^{3,1415}\)
Phương pháp giải
Sử dụng tính chất so sánh lũy thừa: Nếu 0 < a < 1 thì \({a^m} > {a^n} \Leftrightarrow m < n\)
Hướng dẫn giải
Vì \(0<0,3<1\) và \(0,5<\dfrac 2 3 < 3,1415<\pi\)
Nên giá trị lớn nhất trong các số là \(0,3^{0,5}\)
Chọn B
7. Giải bài 2.12 trang 104 SBT Giải tích 12
Tìm số nhỏ nhất trong các số: \(\sqrt{2^\pi}\); \(1,9^\pi\); \(\left(\dfrac 1 {\sqrt 2}\right)^\pi\); \(\pi ^\pi\)
A. \(\sqrt{2^\pi}\)
B. \(1,9^\pi\)
C. \(\left(\dfrac 1 {\sqrt 2}\right)^\pi\)
D. \(\pi ^\pi\)
Phương pháp giải
Sử dụng so sánh lũy thừa: Nếu n > 0 thì \({a^n} < {b^n} \Leftrightarrow a < b\)
Hướng dẫn giải
Ta có: \(\dfrac 1{\sqrt 2}<\sqrt 2<1,9<\pi\)
Số nhỏ nhất trong các số là \(\sqrt{2^\pi}\)
Chọn A.
8. Giải bài 2.13 trang 104 SBT Giải tích 12
Tìm khẳng định đúng trong các khẳng định sau :
A. \(5^{-2}>5^{-0,7}\)
B. \(5^{\frac 1 3}<\left(\dfrac 1 5 \right)^{2,1}\)
C. \(2^\pi > e^\pi\)
D. \(\pi ^{\frac 1 2}>1\)
Phương pháp giải
Nhận xét tính đúng sai của từng đáp án, sử dụng tính chất so sánh lũy thừa:
+) Nếu a > 1 thì \({a^m} > {a^n} \Leftrightarrow m > n\)
+) Nếu \(n > 0,n \notin \mathbb{Z}\) thì \({a^n} > {b^n} \Leftrightarrow a > b > 0\)
Hướng dẫn giải
\(\left\{\begin{align} &5> 1\\& -2<-0,7\\ \end{align}\right.\Rightarrow 5^{-2}<5^{-0,7}\)
A - sai
\(\left(\dfrac 1 5\right)^{2,1}=5^{-2,1}\\ \left\{\begin{align} &5> 1\\&\dfrac 1 3 > -2,1\\ \end{align}\right.\Rightarrow 5^{\frac 1 3}>5^{-2,1}\)
B - sai
\(e\approx 2,71>2\Rightarrow 2^\pi < e^\pi\)
C - sai
\(\pi^{\frac 1 2}>1^{\frac 1 2}=1\)
D - đúng
Chọn D.
9. Giải bài 2.14 trang 104 SBT Giải tích 12
Tìm khẳng định sai trong các khẳng định sau :
A. \(0,5 ^{-\frac 2 3}> 0,6^{-\frac 2 3}\)
B. \(36^{-\frac 4 5}< \pi^{-\frac 4 5}\)
C. \(e^{\frac 1 2}<2\)
D. \((\sqrt 2 ) ^{-\frac 3 4}<1\)
Phương pháp giải
Nhận xét tính đúng sai của từng đáp án, sử dụng tính chất so sánh lũy thừa:
+) Nếu a > 1 thì \({a^m} > {a^n} \Leftrightarrow m > n\)
+) Nếu \(n > 0,n \notin \mathbb{Z}\) thì \({a^n} > {b^n} \Leftrightarrow a > b > 0\)
Hướng dẫn giải
\(0<0,5<0,6<1\) nên \(0,5 ^{-\frac 2 3}>0,6^{-\frac 2 3}\)
A - đúng
\(36> \pi>1\Rightarrow 36^{-\frac 4 5}> \pi^{-\frac 4 5}\)
B - sai
\(e< 4\Rightarrow e^{\frac 1 2 }< 4^{\frac 1 2}=2\)
C - đúng
\(\sqrt 2 > 1 \Rightarrow (\sqrt 2)^{-\frac 3 4}<1\)
D - đúng
Chọn B
Các em hãy luyện tập bài trắc nghiệm Hàm số lũy thừa Toán 12 sau để nắm rõ thêm kiến thức bài học.
Tham khảo thêm
- doc Giải bài tập SBT Toán 12 Bài 1: Lũy thừa
- doc Giải bài tập SBT Toán 12 Bài 3: Lôgarit
- doc Giải bài tập SBT Toán 12 Bài 4: Hàm số mũ. Hàm số lôgarit
- doc Giải bài tập SBT Toán 12 Bài 5: Phương trình mũ và phương trình lôgarit
- doc Giải bài tập SBT Toán 12 Bài 6: Bất phương trình mũ và bất phương trình lôgarit



