Toán 5 Chương 3 Bài: Diện tích hình tam giác

(7)
136 lượt xem
Share

eLib xin giới thiệu đến các em nội dung bài giảng dưới đây do eLib tổng hợp và biên soạn. Bài học sẽ cung cấp cho các em kiến thức về Diện tích hình tam giác, cùng với các bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng hiểu bài hơn.

Mục lục nội dung

Toán 5 Chương 3 Bài: Diện tích hình tam giác

1. Tóm tắt lý thuyết

- Cho hai hình tam giác bằng nhau (xem hình vẽ)

- Lấy một hình tam giác đó, cắt theo đường cao để thành hai mảnh tam giác 1 và 2.

- Ghép hai mảnh 1 và 2 vào hình tam giác còn lại để được hình chữ nhật ABCD (xem hình vẽ).

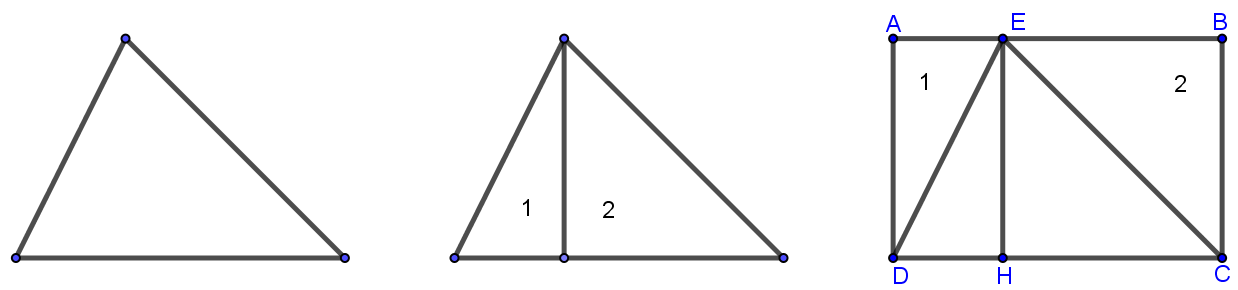
Dựa vào hình vẽ, ta có:

  • Hình chữ nhật ABCD có chiều dài bằng độ dài đáy DC của hình tam giác EDC, có chiều rộng bằng chiều cao EH của hình tam giác EDC
  • Diện tích hình chữ nhật ABCD gấp 2 lần diện tích tam giác EDC.
  • Diện tích hình chữ nhật ABCD là DC x AD = DC x EH.
  • Vậy diện tích hình tam giác EDC là S = DC x EH: 2

Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.

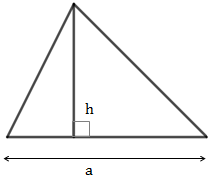
 \(S = \frac{{axh}}{2}\)

S là diện tích, a là độ dài đáy, h là chiều cao

2. Bài tập minh họa

Câu 1: Tính diện tích hình tam giác có:

a) Độ dài đáy là 12cm và chiều cao là 8cm

b) Độ dài đáy là 3,5dm và chiều cao là 1,5dm

Hướng dẫn giải

a) Diện tích hình tam giác: \(\frac{12x8}{2}\)= 48 cm2

b) Diện tích hình tam giác: \(\frac{3,5 x 1,5}{2}\) = 2.625 dm2

Câu 2: Hai cạnh góc vuông của một hình tam giác vuông dài tất cả là 60,5cm. Cạnh góc vuông này bằng  \(S = \frac{2}{3}\) cạnh góc vuông kia.

a) Tính độ dài mỗi cạnh góc vuông.

b) Tính diện tích tam giác vuông đó.

Hướng dẫn giải

a) Cạnh góc vuông này bằng \(S = \frac{2}{3}\) cạnh góc vuông kia, như vậy tổng hai cạnh là 5 phần bằng nhau, nên độ dài mỗi cạnh góc vuông lần lượt là

\(\frac{60,5x2}{5}\)=24,2 (cm)

60,5 - 24,2 = 36,3 (cm)

b)

Áp dụng công thức

S= \(\frac{1}{2}\)a x h = \(\frac{1}{2}\) x 24,2 x 36,2=12,1 . 36,2 = 438,02 (cm2)

Câu 3: Cho tam giác ABC (như hình vẽ) có độ dài đáy BC = 16, diện tích tam giác là 200 cm2. Vẽ chiều cao AH và tính AH.


                                                                                   

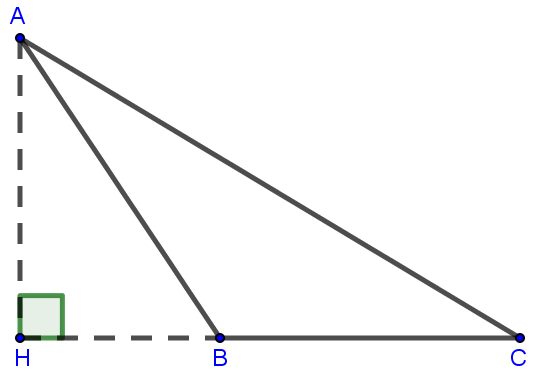
Hướng dẫn giải

Đáy là BC thì chiều cao là đoạn thẳng xuất phát từ A và vuông góc với BC.

Áp dụng công thức tính chiều cao h = S x 2 : a.

Độ dài chiều cao AH là:    200 x 2 : 16 = 25 (cm)

Đáp số: 25 cm

3. Kết luận

Qua bài học này, các em cần nắm được những nội dung sau:

  • Biết cách tính diện tích hình tam gáic.
  • Rèn luyện tính cẩn thận, trình bày sạch đẹp, khoa học.
(7)
136 lượt xem
Share
Ngày:25/08/2020 Chia sẻ bởi:ngan
TẢI VỀ XEM ONLINE

CÓ THỂ BẠN QUAN TÂM