Toán 11 Chương 1 Bài 8: Phép đồng dạng
Bài học Phép đồng dạng bao gồm kiến thức thức cần nhớ và các dạng Toán liên quan được eLib tóm tắt một cách chi tiết, dễ hiểu. Sau đây mời các em cùng tham khảo.
Mục lục nội dung

Toán 11 Chương 1 Bài 8: Phép đồng dạng
1. Tóm tắt lý thuyết
1.1. Định nghĩa phép đồng dạng
- Phép biến hình F gọi là phép đồng dạng tỉ số k (k>0) nếu với hai điểm M, N bất kì và ảnh M’, N’ của chúng ta có:
M′N′=k.MN
{F(M)=M′F(N)=N′⇒M′N′=k.MN(k>0)
- Nhận xét:
- Phép dời hình là phép đồng dạng tỉ số k=1.
- Phép vị tự V(I,k) là phép đồng dạng tỉ số |k|.
- Mối quan hệ giữa phép dời hình, phép vị tự, phép đồng dạng có thể biểu diễn bằng sơ đồ sau:
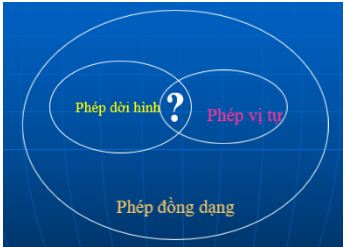
Chú ý: Cho phép vị tự V(I;k). Phép dời hình D
.JPG)
Ta nó rằng F là phép hợp thành của hai phép biến hình V và D. Hoặc có thể nói F là tích của hai phép biến hình V và D.
Kí hiệu: F=D.V.
- Vậy để xác định ảnh của một điểm M qua phép biến hình tích F=D.V ta làm như sau:
- Xác định ảnh của M qua phép vị tự V được ảnh M1.
- Xác định ảnh của M1 qua phép dời hình D ta được M’.
Ta được M’ là ảnh của M qua phép biến hình F=D.V.
1.2. Định lý
Mọi phép đồng dạng F tỉ số k đều là hợp thành của một phép vị tự V tỉ số k và một phép dời hình D.
1.3. Tính chất của phép đồng dạng
Từ định lý trên, ta có các hệ quả sau:Phép đồng dạng tỉ số k:
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
- Biến đường thẳng thành đường thẳng.
- Biến tia thành tia.
- Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k (k là tỉ số phép đồng dạng).
- Biến tam giác thành tam giác đồng dạng tỉ số k.
- Biến đường tròn có bán kính R thành đường tròn có bán kính kR.
- Biến góc thành góc bằng nó.
Nhận xét:
- Ta thấy phép vị tự có tính chất “biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó”.
- Trong trường hợp tổng quát phép dời hình không có tính chất đó.
Ví dụ: Phép quay với một góc quay khác kπ.
Mà phép đồng dạng là hợp thành của phép vị tự và phép dời hình nên cũng không có tính chất “biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó”.
1.4. Hai hình đồng dạng
- Có phép vị tự V biến hình H thành hình H1, có phép biến hình D biến hình H1 thành hình H’.
- Nếu gọi F là phép hợp thành của V và D thì F là phép đồng dạng biến H thành H’.
- Ta nói rằng hai hình H và H’ đồng dạng với nhau.
Định nghĩa: Hai hình gọi là đồng dạng nếu có phép đồng dạng biến hình này thành hình kia.
So sánh phép dời hình, vị tự V(O,k), đồng dạng tỉ số k
- Giống nhau:
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng (và không làm thay đổi thứ tự của ba điểm đó).
- Biến đường thẳng thành đường thẳng, tia thành tia, biến góc thành góc bằng nó.
- Sự khác nhau:
+ Phép dời hình
- Biến đoạn thẳng thành đoạn thẳng bằng nó.
- Biến tam giác thành tam giác bằng tam giác đó.
- Biến đường tròn thành đường tròn có bán kính bằng đường tròn đã cho.
+ Phép vị tự
- Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với |k|.
- Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là |k|.
- Biến đường tròn thành đường tròn có bán kính có bán kính là |k|R.
+ Phép đồng dạng
- Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k.
- Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là k.
- Biến đường tròn thành đường tròn có bán kính có bán kính là kR.
2. Bài tập minh họa
Câu 1: Cho đường thẳng d:x−y+1=0, viết phương trình d’ là ảnh của đường thẳng d qua phép đồng dạng bằng cách thực hiện qua phép vị tự tâm I(1;1), tỉ số k=2 và phép tịnh tiến theo vectơ →v=(−2;−1).
Hướng dẫn giải
Ta có M(0;1)∈d
Qua phép vị tự tâm I, tỉ số k=2 ta có: V(I;2)(d)=d1.
Suy ra phương trình d1 có dạng: x−y+c=0.
Mặt khác: V(I;2)(M)=M1(x1;y1)∈d1
⇒→IM1=2.→IM⇒M1(−1;1).
Vậy d1:x−y+2=0.
Qua phép tịnh tiến theo vectơ →v,ta có: T→V(d1)=d2
Suy ra phương trình d2 có dạng: x−y+d=0.
Mặt khác: M1∈d1⇒T→v(M1)=M2(x2;y2)∈d2
⇒→M1M2=→v⇒M2(−2;1).
Vậy d2 có phương trình: x−y+3=0.
Qua phép đồng dạng đường thẳng d:x−y+1=0 trở thành đường thẳng d2:x−y+3=0.
Câu 2: Cho đường tròn (C):(x−1)2+(y−2)2=4. Xác định ảnh của (C) qua phép vị tự tâm O, tỉ số k=-2 và phép đối xứng trục Oy.
Hướng dẫn giải
(C) có tâm I(1;2) bán kính R=2.
Gọi I’ và R’ lần lượt là tâm và bán kính của (C’) là ảnh của (C) qua phép vị tự tâm O, tỉ số k=-2.
Suy ra: R’=4.
Ta có: V(O;−2)(I)=I′⇒→OI′=−2→OI⇒I′(−2;−4)
Vậy phương trình của (C’) là: (x+2)2+(y+4)2=16.
Gọi I’’, R’’ lần lượt là tâm và bán kính của đường tròn (C’’) là ảnh của (C’) qua phép đối xứng trục Oy.
Suy ra: R″=4.
I’’=ĐOy(I’)⇒{xI″=−xI′=2yI″=yI′=−4
Vậy phương trình (C’’) là: (x−2)2+(y+4)2=16.
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho đường thẳng viết phương trình d’ là ảnh của đường thẳng d qua phép đồng dạng bằng cách thực hiện qua phép vị tự tâm I(-1;2), tỉ số k=1 và phép tịnh tiến theo vectơ →v=(1;3).
Câu 2: Cho đường tròn (C):(x+1)2+(y+2)2=16. Xác định ảnh của (C) qua phép vị tự tâm O, tỉ số k=12 và phép đối xứng trục Oy.
3.2. Bài tập trắc nghiệm
Câu 1: Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Câu 2: Trong mặt phẳng tọa độ Oxy phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 1/2 và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ.
A. (2;-1)
B. (8;1)
C. (4;-2)
D. (8;4)
Câu 3: Cho hình thoi ABCD tâm O. Gọi E, F, M, N lần lượt là trung điểm các cạnh AB, CD, BC, AD. P là phép đồng dạng biến tam giác OCF thành tam giác CAB. Tìm mệnh đề sai trong các mệnh đề sau:
A. P hợp thành bởi phép đối xứng tâm O và phép vị tự tâm A tỉ số k = 2
B. P hợp thành bởi phép đối xứng trục AC và phép vị tự tâm C tỉ số k = 2
C. P hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm O
D. P hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O tỉ số k = -1
Câu 4: Trong mặt phẳng Oxy, cho đường tròn (C):x2+y2−2x−2y−2=0. Gọi (C’) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O góc 900 và phép vị tự tâm O tỉ số -2. Phương trình của (C’) là:
A. x2+y2−4x−4y−8=0.
B. x2+y2−4x+4y−8=0.
C. x2+y2+4x−4y−8=0.
D. x2+y2+4x+4y−8=0.
Câu 5: Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Khẳng định nào sau đây là đúng?
A. Hai hình thang ILKI và IHDC đồng dạng với nhau theo tỉ số k=14.
B. Hai hình thang ILKI và IHDC đồng dạng với nhau theo tỉ số k=12.
C. Hai hình thang ILKI và IHDC đồng dạng với nhau theo tỉ số k=23.
D. Hai hình thang ILKI và IHDC không đồng dạng với nhau.
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Phép đồng dạng Toán 11 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này các em cần nắm được những nội dung sau:
- Định nghĩa, tính chất của phép đồng dạng.
- Phương pháp giải các dạng bài tập liên quan đến phép đồng dạng.
Tham khảo thêm
- docx Toán 11 Chương 1 Bài 1: Phép biến hình
- docx Toán 11 Chương 1 Bài 2: Phép tịnh tiến
- docx Toán 11 Chương 1 Bài 3: Phép đối xứng trục
- docx Toán 11 Chương 1 Bài 4 Phép đối xứng tâm
- docx Toán 11 Chương 1 Bài 5: Phép quay
- docx Toán 11 Chương 1 Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- docx Toán 11 Chương 1 Bài 7: Phép vị tự



.JPG)

