Toán 7 Chương 3 Bài 7: Tính chất đường trung trực của một đoạn thẳng

Định lý 1: (Định lý thuận): Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

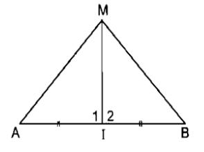
Ví dụ: Vì điểm M nằm trên đường trung trực của đoạn thẳng AB nên MA = MB.

Định lý 2: (Định lý đảo): Điểm cách đều hai mút của một đoạn thẳng thì năm trên đường trung trực của đoạn thẳng đó.

Ví dụ: Vì MA = MB nên điểm M nằm trên đường trung trực của đoạn thẳng AB.

Nhận xét: Từ định lý thuận và định lý đảo ta có: tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.

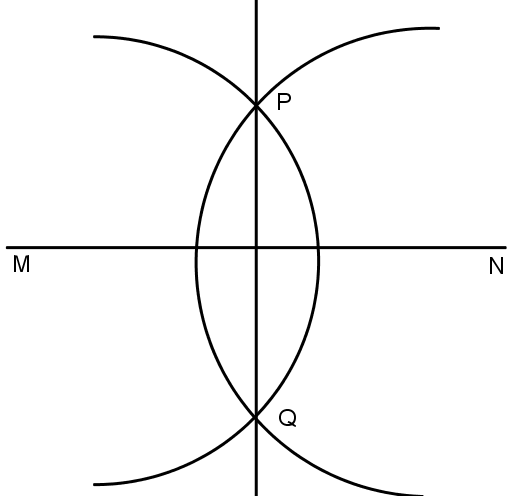
Vẽ đường trung trực của đoạn thẳng MN bằng thước thẳng và compa; như sau:

• Lấy M làm tâm vẽ cung tròn có bán kính lớn hơn \(\frac{1}{2}MN\). Lấy N làm tâm vẽ cung tròn có cùng bán kính đó.
• Hai cung tròn này có hai điểm chung là P, Q.
• Dùng thước vẽ đường thẳng PQ. Đó đường trung trực của đoạn thẳng MN.

Câu 1: Tam giác ABC có AC > AB, phân giác AD. Trên AC lấy điểm E sao cho AE=AB. Chứng minh rằng AD vuông góc với BE.

Hướng dẫn giải

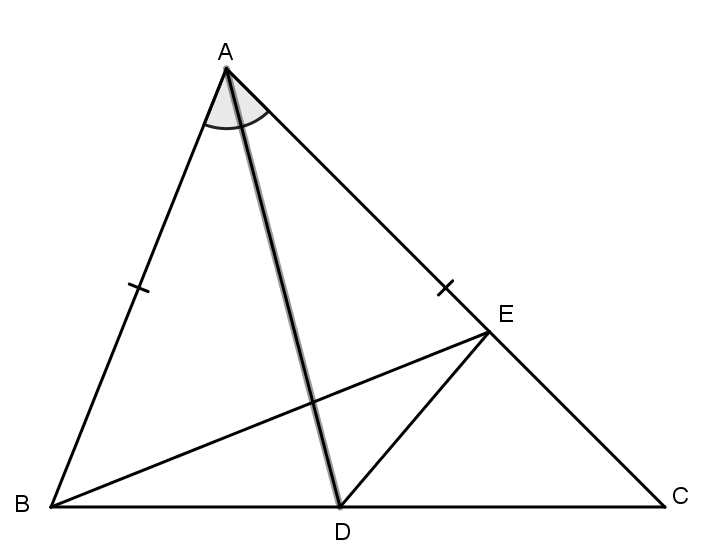
Nối BE và ED

Xét \(\Delta ADB\) và \(\Delta ADE\) có:

AB = AE (gt)

\(\widehat {BAD} = \widehat {EAD}\) (AD là tia phân giác \(\widehat {BAC}\)).

AD cạnh chung

Vậy \(\Delta ADB = \Delta ADE\,\,(c.g.c)\)

Suy ra DB = DE

Lại có AB = AE

Do đó AB là đường trung trực của BE.

Vậy \(AD \bot BE.\)

Câu 2: Cho \(\Delta ABC.\) Hãy tìm một điểm cách đều hai cạnh AB, AC và cách đều hai đỉnh A, B.

Hướng dẫn giải

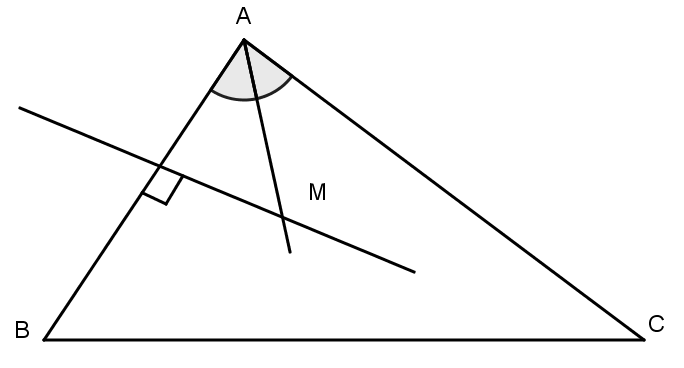
Mọi điểm trên đường phân giác của góc A thì cách đều hai cạnh AB, AC.

Mọi điểm trên đường trung trực của AB thì cách đều hai điểm A, B.

Vậy điểm M cần tìm là giao điểm của đường phân giác và đường trung trực nói trên.

Câu 3: Cho m là đường trung trực của đoạn thẳng AB, C là điểm thuộc m. Gọi Cx là tia đối của tia CA, Cn là tia phân giác của góc BCx. Chứng minh rằng Cn vuông góc với m.

Hướng dẫn giải

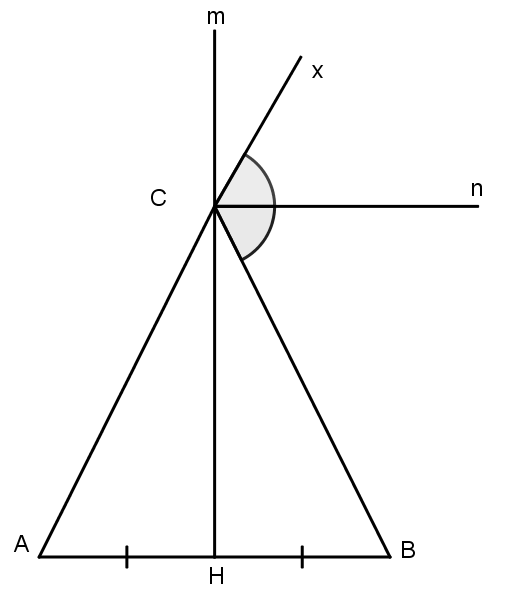
Gọi H là giao điểm của m và AB.

Xét \(\Delta AHC\) và \(\Delta BHC\) có HA = HB (H là điểm nằm trên đường trung trực của AB)

\(\widehat {AHC} = \widehat {AHC} = {90^0}\)

CH là cạnh chung

Nên \(\Delta AHC = \Delta BHC\) (c.g.c)

Suy ra \(\widehat {ACH} = \widehat {BCH}\)

Nên CH là tia phân giác của \(\widehat {ACB}\)

Cn là tia phân giác của \(\widehat {BCx}\) (gt)

Như vậy m và Cn là hai tia phân giác của hai góc kề bù ACB và BCx nên \({C_n} \bot m.\)

Câu 1: Chứng minh rằng không tồn tại điểm cách đều, ba điểm thẳng hàng.

Câu 2: Cho đoạn thẳng AB thuộc nửa mặt phẳng bờ d. Xác định điểm M thuộc d sao điểm M cách đều hai điểm A, B.

Câu 3: Trên đường trung trực d của đoạn thẳng AB lấy điểm M. Hạ \(MH \bot AB.\) Trên đoạn MH lấy điểm P. Gọi E là giao điểm của AP với MB. Gọi F là giao điểm của BP với MA.

a) Chứng minh MH là phân giác góc AMB

b) Chứng minh MH là trung trực của đoạn thẳng EF

c) Chứng minh AF = BE.

Câu 1: Cho tam giác ABC vuông tại A, có \(\widehat C = {30^0}\), đường trung trực của BC cắt AC tại M. Hãy chọn câu đúng 

A. BM là đường trung tuyến của tam giác ABC

B. BM = AB

C. BM là phân giác của góc ABC

D. BM là đường trung trực của tam giác ABC

Câu 2: Cho tam giác ABC cân tại, có \(\widehat A = {40^0}\), đường trung trực AB cắt BC ở D. Tính số đo góc CAD

A. 30⁰

B. 45⁰

C. 60⁰

D. 40⁰

Câu 3: Gọi O là giao điểm của ba đường trung trực trong tam giác ABC. Khi đó O là:

A. Điểm cách đều ba cạnh của tam giác ABC

B. Điểm cách đều ba đỉnh của tam giác ABC

C. Tâm đường tròn ngoại tiếp tam giác ABC

D. Đáp án B và C đúng

Câu 4: Nếu một tam giác có một đườngtrung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?

A. Tam giác vuông 

B. Tam giác cân

C. Tam giác đều

D. Tam giác vuông cân

Câu 5: Cho tam giác ABC cân ở A. Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của góc ACB. Tính các góc của tam giác ABC

A. \(\widehat A = {30^0},\widehat B = \widehat C = {75^0}\)

B. \(\widehat A = {40^0},\widehat B = \widehat C = {70^0}\)

C. \(\widehat A = {36^0},\widehat B = \widehat C = {72^0}\)

D. \(\widehat A = {70^0},\widehat B = \widehat C = {55^0}\)

Qua bài học này, các em cần nắm được những nội dung sau:

• Hiểu được định nghĩa đường trung trực của một đoạn thẳng.
• Nắm được tính chất của các điểm thuộc đường trung trực.
• Áp dụng làm được những bài toán liên quan.