Toán 7 Chương 3 Bài 6: Tính chất ba đường phân giác của tam giác
eLib xin dưới thiệu đến các em nội dung bài giảng Tính chất ba đường phân giác của tam giác do eLib tổng hợp và biên soạn dưới đây. Bài học sẽ giúp các em tìm hiểu về Tính chất ba đường phân giác của tam giác, cùng với những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng nắm đươc nội dung phần này.
Mục lục nội dung

Toán 7 Chương 3 Bài 6: Tính chất ba đường phân giác của tam giác
1. Tóm tắt lý thuyết
1.1. Đường phân giác của tam giác
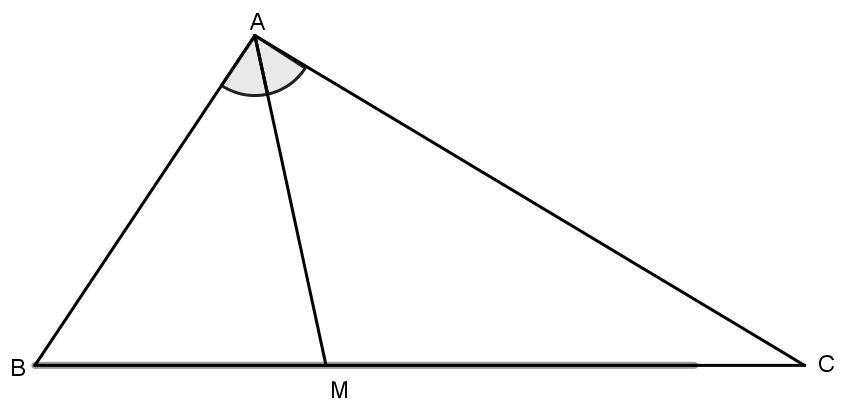
- Trong tam giác ABC tia phân giác của góc A cắt cạnh BC tại điểm M.
- Đoạn thẳng AM được gọi là đường phân giác của tam giác ABC.
- Đường thẳng AM cũng gọi là đường phân giác của tam giác ABC.
- Mỗi tam giác có ba đường phân giác.
- Tính chất: Trong một tam giá cân đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến ứng với cạnh đáy.
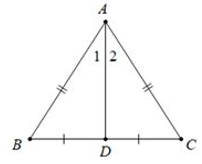
Ví dụ:
Xét tam giác ABC có:
{AB=AC^A1=^A2⇒BD=DC
1.2. Tính chất ba đường phân giác của tam giác
Định lý: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
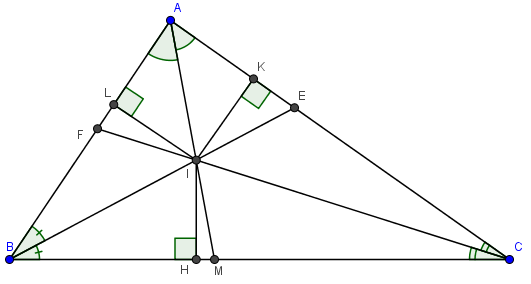
Ví dụ: Tam giác ABC có ba đường phân giác giao nhau tại I, khi đó: ID=IE=IF
2. Bài tập minh họa
Câu 1: Cho tam giác ABC hai đường thẳng phân giác trong của hai góc ˆB và ˆCcắt nhau ở điểm I và hai đường phân giác ngoài của hai góc ấy cắt nhau ở điểm D. Chứng minh rằng ba điểm A, I, D thẳng hàng.
Hướng dẫn giải
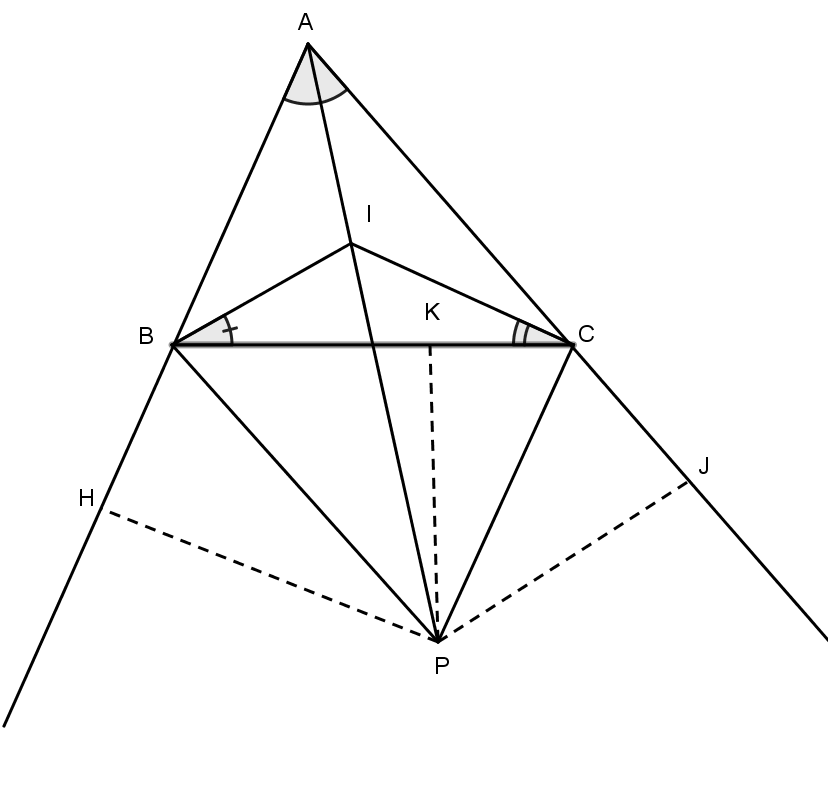
Hai phân giác trong của hai góc ˆB và ˆCcắt nhau tại I nên I phải thuộc phân giác góc ˆA
Từ D hạ DH, DK, DJ vuông góc lần lượt với AB, BC, AC.
Ta có: DH = DK (do D thuộc phân giác ngoài của góc B)
Tương tự: DK=DJ⇒DH=DJ
Điều này chứng tỏ D thuộc phân giác góc A hay D thuộc AD.
Vậy A, I, D thẳng hàng.
Câu 2: Tam giác ABC có trung tuyến AM đồng thời là phân giác. Chứng minh rằng tam giác đó là tam giác cân.
Hướng dẫn giải
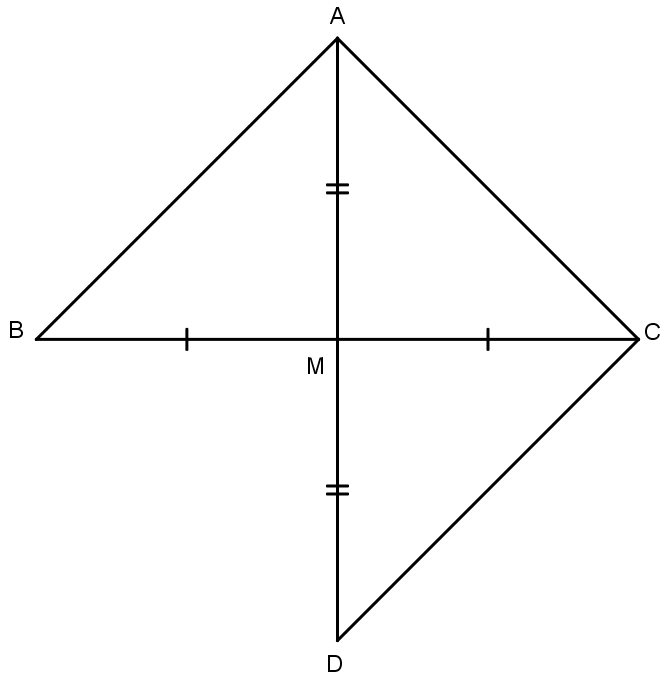
Kéo dài AM một đoạn MD = AM
ΔAMB và ΔDMC có:
AM = DM (cách vẽ)
^AMB=^DMC (đối đỉnh)
MB = MC (gt)
Nên ΔAMB=ΔDMC (c.g.c)
Suy ra ^A1=ˆD;AB=CD (1)
Ta có ^A1=^A2(gt),^A1=ˆD⇒^A2=ˆD
Do đó ΔACD suy ra AC=CD (2)
Từ (1) và (2) suy ra AB = AC
Vậy ΔABClà tam giác cân.
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Hai đường phân giác của góc B và C trong tam giác ABC cắt nhau ở I. Chứng minh rằng: ^BIC=90+ˆA2.
Câu 2: Cho tam giác vuông ABC (ˆA=900). Trên cạnh AC lấy điểm D sao cho ^ABC=3^ABD. Trên cạnh AB lấy điểm E sao cho ^ACB=3^ACE. Gọi F là giao điểm của BD và CE; I là giao điểm của ba đường phân giác của tam giác BFC.
a) Tính ^BFC.
b) Chứng tỏ rằng tam giác DEI là tam giác đều.
Câu 3: Cho ΔABC. Gọi I là giao điểm của hai tia phân giác hai góc A và B. Qua I vẽ đường thẳng song song với BC, cắt AB tại M, cắt AC tại N. Chứng minh rằng: MN = BM + CN.
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC, các tia phân giác của góc B và A cắt nhau tại điểm O. Qua O kẻ đường thẳng song song với BC cắt AB tại M, cắt AC tại N. Cho BM = 2cm, CN = 3cm. Tính MN
A. 5cm
B. 6cm
C. 7cm
D. 8cm
Câu 2: Chọn phát biểu đúng nhất
A. Ba tia phân giác của một tam giác cùng đi qua một điểm. Điểm đó gọi là trọng tâm của tam giác
B. Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác
C. Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy
D. Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó
Câu 3: Điểm E nằm trên tia phân giác góc A của tam giác ABC ta có:
A. E nằm trên tia phân giác góc B
B. E cách đều hai cạnh AB, AC
C. E nằm trên tia phân giác góc C
D. EB = EC
Câu 4: Cho tam giác ABC có hai đường phân giác CD và BE cắt nhau tại I. Khi đó
A. AI là trung tuyến vẽ từ A
B. AI là đường cao kẻ từ A
C. AI là trung trực cạnh BC
D. AI là phân giác của góc A
Câu 5: Cho tam giác ABC có ˆA=700, các đường phân giác BE và CD của góc B và góc C cắt nhau tại I. Tính ^BIC
A. 1250
B. 1000
C. 1050
D. 1400
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Hiểu được định nghĩa, tính chất đường phân giác của tam giác.
- Áp dụng làm được những bài toán liên quan.
Tham khảo thêm
- doc Toán 7 Chương 3 Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- doc Toán 7 Chương 3 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- doc Toán 7 Chương 3 Bài 3: Quan hệ giữa ba cạnh của một tam giác Bất đẳng thức tam giác
- doc Toán 7 Chương 3 Bài 4: Tính chất ba đường trung tuyến của tam giác
- doc Toán 7 Chương 3 Bài 5: Tính chất tia phân giác của một góc
- doc Toán 7 Chương 3 Bài 7: Tính chất đường trung trực của một đoạn thẳng
- doc Toán 7 Chương 3 Bài 8: Tính chất ba đường trung trực của tam giác
- doc Toán 7 Chương 3 Bài 9: Tính chất ba đường cao của tam giác