Toán 8 Chương 1 Bài 6: Đối xứng trục

Định nghĩa: Hai điểm đối xứng nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm ấy.

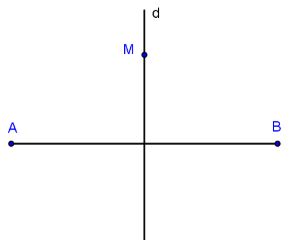
Ví dụ: A và B đối xứng qua d \( \Leftrightarrow \) d là trung trực của AB

Nếu điểm \(M \in d\) thì điểm đối xứng với M qua d cũng chính là điểm M.

a. Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng qua d với một điểm thuộc hình kia và ngược lại.

b. Tính chất:

Định lý: Nếu hai đoạn thẳng AB và A’B’ có các điểm A và A’, B và B’ đối xứng nhau qua đường thẳng d thì hai đoạn thẳng đó bằng nhau và đối xứng với nhau qua đường thẳng d.

c. Chú ý: Ta có

Hình đối xứng qua một đường thẳng d của:

- Một đường thẳng là một đường thẳng

- Một đoạn thẳng là một đoạn thẳng

- Một góc là một góc bằng nó

- Một tam giác là một tam giác bằng nó.

- Một đường tròn là một đường tròn có bán kính bằng bán kính đường tròn đã cho.

a. Định nghĩa: Đường  thẳng d gọi là trục đối xứng của hình F nếu điểm đối xứng của mỗi điểm của mỗi hình F qua đường thẳng d cũng thuộc hình F.

b. Một số trục đối xứng quen thuộc

- Một đoạn thẳng có trục đối xứng là đường trung trực của đoạn thẳng ấy.

- Một góc có trục đối xứng là tia phân giác của góc.

- Hai đường thẳng giao nhau có trục đối xứng là hai đường thẳng chứa các phân giác của các góc do hai đường thẳng tạo nên; hai trục đối xứng này vuông góc với nhau.

- Tam giác cân có một trục đối xứng là đường cao cũng là phân giác, trung tuyến, thuộc cạnh đáy. Tam giác đều có ba trục đối xứng.

- Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm của hai đáy.

Câu 1: Cho hai điểm A, B nằm trong hai nửa mặt phẳng đối nhau, bờ là đường thẳng a cho trước. Tìm trên đường thẳng a một điểm sao cho hiệu các khoảng cách từ M đến hai điểm A, B có giá trị lớn nhất.

Hướng dẫn giải

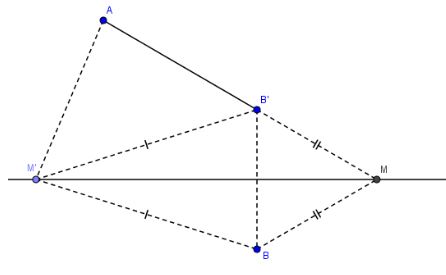
Gọi B’ là điểm đối xứng với điểm B qua đường thẳng a.

Nối AB’ đường thẳng AB’ cắt đường thẳng a tại điểm M. Đó chính là điểm M cần tìm.

Vì MB = MB’ và ba điểm A, B’, M thẳng hàng nên:

|MA – MB| = |MA – MB’| = AB’

Ta chứng minh rằng với mọi điểm \(M' \in a\) mà \(M' \ne M\) thì hiệu:

|M’A – M’B| > |MA – MB|

Thật vậy, ta có M’B’ = M’B, suy ra:

|M’A – M’B| = |M’A – M’B’|

Trong tam giác AM’B’, theo bất đẳng thức tam giác, ta có:

\(\left| {M'A - M'B'} \right| \le \left| {MA - MB} \right|\)

Dấy “=” xảy ra chỉ khi M’ trùng với M.

Chú ý: Trường hợp đặc biệt, khi AB’ song song với a, tức là hai điểm A, B cách đều đường thẳng a thì điểm M cần tìm là giao điểm của AB với đường thẳng a.

Câu 2: Cho góc nhọn xOy và một điểm M thuộc miền ngoài của góc ấy.

Gọi: \({M_1}\) là điểm đối xứng của M qua Ox

        \({M_2}\) là điểm đối xứng của M qua Oy

         I là trung điểm của đoạn thẳng \({M_1}{M_2}.\)

a. Xác định trục đối xứng mà qua đó \({M_1}\)và \({M_2}\) là hai điểm đối xứng với nhau.

b. Hai tia OM và OI đối xứng với nhau qua trục là đường thẳng nào?

Hướng dẫn giải

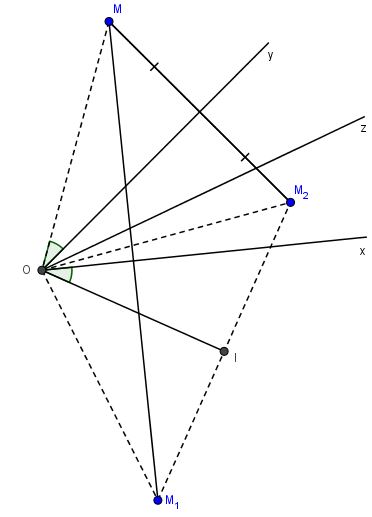
a. M và \({M_1}\)là đối xứng với nhau qua Ox   

\( \Rightarrow O{M_1} = OM\)

M và \({M_2}\)là đối xứng với nhau qua Oy

\( \Rightarrow O{M_2} = OM\)

Vậy \(O{M_1} = O{M_2}\)

\( \Rightarrow \Delta O{M_1}{M_2}\) cân;

Vậy OI là đường trung trực của \({M_1}{M_2}.\)

b. Kẻ tia phân giác Oz của góc xOy.

Dễ thấy \(\widehat {{M_1}OM} = \widehat {2MOx} = 2(\widehat {MOy} + \widehat {xOy})\)

\(\begin{array}{l}\widehat {{M_2}OM} = 2\widehat {MOy}\\ \Rightarrow \widehat {{M_1}O{M_2}} = 2\widehat {xOy}.\end{array}\)

Từ đây, ta có: \(\widehat {{M_1}OI} = \frac{1}{2}\widehat {{M_1}O{M_2}} = \widehat {xOy}\) (1)

Ta cũng có \(\widehat {{M_1}Ox} = \widehat {MOx}\)   (2)

Từ (1) và (2) suy ra \(\widehat {IOx} = \widehat {MOy}\)   (3)

Vì Oz là tia phân giác của xOy, nên \(\widehat {xOz} = \widehat {yOz}\)   (4)

Từ (3) và (4) ta có: \(\widehat {MOz} = \widehat {IOz}\)

Vậy Oz là tia phân giác của góc \(\widehat {MOI}\) hay OM và OI đối xứng với nhau qua Oz.

Câu 3: Cho tam giác ABC vuông góc tại đỉnh A. Kẻ đường cao AH. Gọi D, E theo thứ tự là các điểm đối xứng của điểm H qua AB, AC. Chứng minh rằng:

a. Điểm A là trung điểm của đoạn thẳng DE.

b. DE = 2AH.

Hướng dẫn giải

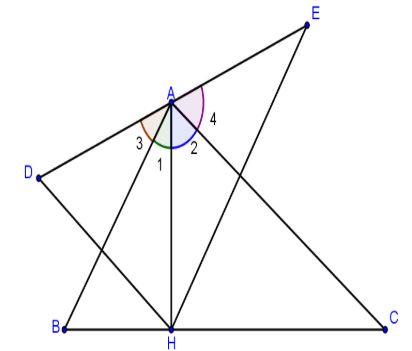
a. D và H đối xứng với nhau qua AB nên AD = AH.

Tam giác DAH cân tại đỉnh A mà \(AB \bot DH\) nên AB cũng là phân giác của góc DAH, suy ra: \(\widehat {{A_1}} = \widehat {{A_3}}\)

Tương tự, ta có AE =AH và  \(\widehat {{A_2}} = \widehat {{A_4}}\)

Từ các kết quả trên ta có:

\(\widehat {{A_3}} + \widehat {{A_1}} + \widehat {{A_2}} + \widehat {{A_4}} = 2(\widehat {{A_1}} + \widehat {{A_2}}) = {2.90^0} = {180^0}\)

\( \Rightarrow \) Ba điểm D, A, E thẳng hàng   (1)

Ta cũng có AD = AE  (2)

Từ (1) và (2) suy ra A là trung điểm của DE.

b. Ta có ngay AD = AH và AE = AH

\(\Rightarrow DE = AD + AE = 2AH\)

Câu 1: Cho tam giác ABC. Kẻ đường cao AH. Gọi D, E theo thứ tự là các điểm đối xứng của điểm H qua các cạnh AB, AC. Đường thẳng DE cắt  AB, AC lần lượt tại M, N. Chứng minh:

a. Tam giác DAE là tam giác cân.

b. HA là phân giác của góc MHN.

c. Ba đường thẳng BN, CM và AH đồng quy.

d. BN, CM là các đường cao của tam giác ABC.

Câu 2: Cho góc nhọn xOy và một điểm A thuộc miền trong của góc ấy. Tìm trên cạnh Ox một điểm B, trên cạnh Oy một điểm C sao cho tam giác ABC có chu vi nhỏ nhất.

Câu 3: Cho hình thang vuông ABCD (AB // CD)

Gọi E, F theo thứ tự các điểm đối xứng của điểm B và điểm A qua đường thẳng DC; G; H theo thứ tự là các điểm đối xứng của điểm C và điểm E qua đường thẳng AD.

a. Chứng minh điểm D là trung điểm của các đoạn thẳng BH.

b. Chứng minh AH // BF và CH // BG.

Câu 1: Chọn phát biểu đúng

A. Hai điểm A,B đối xứng với nhau qua đường thẳng d nếu d đi qua trung điểm của AB

B. Hai điểm A,B đối xứng với nhau qua đường thẳng d nếu d vuông góc với AB

C. Hai điểm A,B đối xứng với nhau qua đường thẳng d nếu d vuông góc với AB tại trung điểm của AB

D. Hai điểm A,B đối xứng với nhau qua đường thẳng d nếu d song song với AB

Câu 2:  Chọn phát biểu sai

Hình đối xứng qua một đường thẳng d của:

A. Một đoạn thẳng là đoạn thẳng bằng nó

B.  Một đường thẳng là một đường thẳng bằng nó

C. Một góc là một góc bằng nó

D.  Một tam giác là một tam giác bằng nó

Câu 3:  Trục đối xứng của hình thang cân là?

A. Đường trung bình của hình thang cân

B. Hai đường chéo của hình thang cân

C. Đường thẳng đi qua trung điểm của  hai đáy

D. Đường thẳng vuông góc với hai đáy

Câu 4: Cho đoạn AB = 5 cm A₁B₁ đối xứng với AB qua d, độ dài  A1B1=?

A. 3 cm

B. 5 cm

C. 10 cm

D.  15 cm

Câu 5: Cho tam giác ABC và tam giác A'B'C'  đối xứng với nhau qua d biết AB = 6cm, AC =8 và chu vi tam giác ABC là 24cm. Hỏi B'C' =?

A. B'C' = 8 cm

B. B'C' = 10 cm

C. B'C' =12 cm

D. B'C' =14 cm

Qua bài học này, các em cần nắm được những nội dung sau:

• Nắm được khái niệm về đối xứng trục, các hình có trục đối xứng và xác định được trục đối xứng.

• Ghi nhớ được tính chất của điểm đối xứng qua trục, hình đối xứng qua trục.

• Vận dụng kiến thức giải được một số bài toán liên quan.