Toán 8 Chương 2 Bài 6: Diện tích đa giác

Phương pháp tính diện tích đa giác

Việc tính diện tích đa giác của một đa giác bất kì thường được quy về việc tính diện tích các tam giác. Ta có thể chia đa giác thành các tam giác hoặc tạo ra một tam giác nào đó chứa đa giác 

Trong một số trường hợp, để việc tính toán thuận lợi ta có thể chia đa giác thành nhiều tam giác vuông và hình thang vuông.

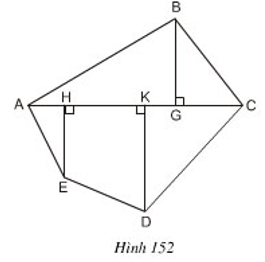
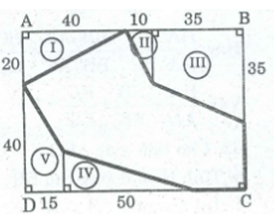
Thực hiện các phép đo cần thiết (chính xác đến từng mm) để tính diện tích hình $ABCDE$ (h.$152$).

Hướng dẫn giải

Đa giác $ABCDE$ được chia thành tam giác $ABC$, hai tam giác vuông $AHE, DKC$ và hình thang vuông $HKDE.$

Thực hiện phép đo chính xác đến mm ta được:

$BG= 19mm, AC = 48mm,$$AH = 8mm, HK = 18mm$

$KC = 22mm, EH = 16mm,$$KD = 23mm$

${S_{ABC}}= \dfrac{1}{2}.BG. AC = \dfrac{1}{2}. 19.48 = 456$ $(m{m^2})$

${S_{AHE}}=\dfrac{1}{2} AH. HE = \dfrac{1}{2} 8.16 = 64$ $(m{m^2})$

${S_{DKC}}=\dfrac{1}{2}. KC.KD = \dfrac{1}{2}. 22.23$$\,= 253$ $(m{m^2})$

${S_{HKDE}}=\dfrac{\left ( HE+KD \right ).HK}{2}$$\,= \dfrac{\left (16+23 \right ).18}{2}= 351$ $(m{m^2})$

Do đó 

${S_{ABCDE}} = {S_{ABC}} + {S_{AHE}} + {S_{DKC}}$$\,+ {S_{HKDE}} = 456 + 64 + 253 + 351$$\,= 1124\;(m{m^2})$

Vậy ${S_{ABCDE}} = 1124\;(m{m^2})$

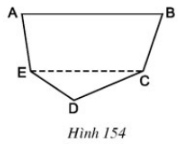
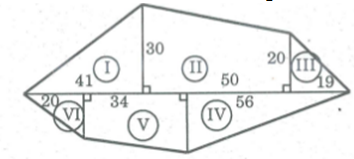
Thực hiện các phép vẽ và đo cần thiết để tính diện tích một đám đất có dạng như hình $154$, trong đó $AB // CE$ và được vẽ tỉ lệ $\dfrac{1}{5000}$

Hướng dẫn giải

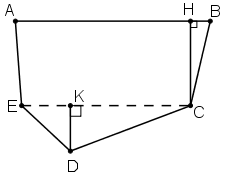
Chia đám đất $ABCDE$ thành hình thang $ABCE$ và tam giác $ECD.$ Cần vẽ đường cao $CH$ của hình thang và đường cao $DK$ của tam giác. Thực hiện các phép đo chính xác đến $mm$ ta được $AB = 30\,mm, CE = 26\,mm,$ $CH = 13\,mm, DK = 7\,mm.$

${S_{ABCE}}=\dfrac{\left ( AB+EC \right ).CH}{2}$$\,= \dfrac{\left ( 30 + 26 \right ).13}{2} =364$ $(m{m^2})$

${S_{ECD}}=\dfrac{1}{2} EC. DK = \dfrac{1}{2} .26.7= 91$ $(m{m^2})$

Do đó ${S_{ABCDE}} = {S_{ABCE}} + {S_{ECD}} = 364 + 91$$\,= 455$ $(m{m^2})$

Vì bản đồ được vẽ với tỉ lệ xích $\dfrac{1}{5000}$  nên diện tích đám đất là:

$S = 455. 5000 = 2275000 \;(m{m^2})$$\,= 2,275 \;({m^2})$

Câu 1: Thực hiện các phép vẽ và đo cần thiết để tính diện tích đa giác $ABCDE$ $(BE // CD)$ (h.189)

Câu 2: Theo kích thước đã cho trên hình 191, hãy tính diện tích hình gạch sọc (đơn vị $m^2$ ).

Câu 3: Tìm diện tích mảnh đất theo kích thước cho trên hình 192 (đơn vị $m^2$)

Câu 1: Số đo mỗi góc trong và ngoài của ngũ giác đều  là:

A. $75^{\circ}; 150^{\circ}$

B. $108^{\circ}; 72^{\circ}$

C. $100^{\circ}; 80^{\circ}$

D. $110^{\circ}; 70^{\circ}$

Câu 2: Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng 3cm. Gọi M là trung điểm của AB. DM cắt AC tại N. Tính diện tích tam giác AMN

A. 4 $cm^{2}$

B. 10 $cm^{2}$

C. 2 $cm^{2}$

D. 1 $cm^{2}$

Câu 3: Cho tam giác ABC có diện tích 12 $cm^{2}$. Gọi N là trung điểm của BC, trên AC sao cho AM = \frac{1}{3}AC, AN cắt BM tại O. Tính diện tích tam giác AOM

A. 2 $cm^{2}$

B. 1 $cm^{2}$

C. 3 $cm^{2}$

D. 6 $cm^{2}$

Câu 4: Cho hình thoi MNPQ. Biết A, B, C, D lần lượt là các trung điểm của các cạnh NM, NP, PQ, QM. Tính tỉ số diện tích của tứ giác ABCD và hình thoi MNPQ.

A. $\frac{1}{2}$

B. $\frac{2}{3}$

C. 2

D. $\frac{1}{3}$

Câu 5: Số đo mỗi góc của hình 9 cạnh đều là:

A. $120^{\circ}$                       

B. $60^{\circ}$                                        

C. $140^{\circ}$                                           

D. $135^{\circ}$

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm vững công thức tính diện tích đa giác đơn giản, đặc biệt là cách tính di ện tích tam giác và hình thang.
• Biết chia một cách hợp lý đa giác cần tìm diện tích thành nhiều đa giác đơn giản.
• Biết thực hiện các phép vẽ và đo cần thiết.