Toán 7 Chương 1 Bài 5: Tiên đề Ơ-clit về đường thẳng song song

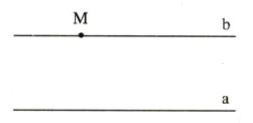
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Ví dụ: Hình vẽ trên: Qua một điểm M ở ngoài đường thẳng a chỉ có một đường thẳng b song song với đường thẳng a.

Nếu một đường thẳng cắt hai đường thẳng song song thì:

• Hai góc so le trong bằng nhau.
• Hai góc đồng vị bằng nhau.
• Hai góc trong cùng phía bù nhau.

Câu 1: Hai đường thẳng x’x và y’y song song với nhau bị cắt bởi một một cát tuyến tại 2 điểm A và B. Gọi At là tia phân giác của $\widehat {xAB}.$

a. Tia At có cắt đường thẳng y’y hay không? Vì sao?

b. Cho $\widehat {xAB} = {80^0}.$ Tính $\widehat {ACB}.$

Hướng dẫn giải

a. Giả sử ta At không cắt y’y

Suy ra AC//y’y. Theo tiên đề Ơclit thì AC trùng với x’x. Điều này vô lý vì vậy tia At phải cắt y’y tại C.

b. Ta có:

$\widehat {xAt} = \frac{1}{2}\widehat {xAB} = \frac{1}{2}{.80^0} = {40^0}$ (At là tia phân giác của $\widehat {xAB}$).

mà $\widehat {xAt} = \widehat {ACB}$ (so le trong)

Vậy $\widehat {ACB} = {40^0}.$

Câu 2: Cho hình bên, biết $\widehat A = {50^0}$ và $\widehat B = {140^0}$, Ax // By’. Chứng minh rằng $\widehat {AOB} = {90^0}.$

Hướng dẫn giải

Kẻ qua O qua đường thẳng Oz // Ax, ta có: $\widehat {AOz} = \widehat {xAO} = 50{}^0$(góc so le trong)

Lại có: $\widehat {OBy} = {150^0}$
$\Rightarrow \widehat {OBy} = {180^0} - {140^0} = {40^0}$
$Oz//Ax \Rightarrow Oz//By$

$\Rightarrow \widehat {BOz'} = \widehat {OBy} = {40^0}$ (góc so le trong)

Do đó: $\widehat {AOz} = \widehat {z'OB} = {50^0} + {40^0} = {90^0}$ hay $\widehat {AOB} = {90^0}.$

Câu 3: Cho hình bên, biết Ax // By. Chứng minh rằng $\widehat A + \widehat B + \widehat C = {360^0}.$

Hướng dẫn giải

Kẻ qua C đường thẳng Cz // Ax ta có:

$\widehat A + \widehat {ACz} = {180^0}$ (góc trong cùng phía bù nhau)

Lại có: $Cz//Ax \Rightarrow Cz//By \Rightarrow \widehat B + \widehat {zCB} = {180^0}$ (góc trong cùng phía bù nhau)

$\Rightarrow \widehat A + \widehat B + \widehat {ACz} + \widehat {zCB} = {360^0}\,\,\,\,hay\,\,\,\,\,\widehat A + \widehat B + \widehat C = {360^0}.$

Câu 1: Cho góc xOy có số đo bằng ${30^0}$. Một điểm A thuộc Ox. Qua A dựng tia A’y // Oy và nằm trong góc xOy.

a. Tính OAy’.

b. Gọi Ot và At’ theo thứ tự là các tia phân giác của các góc xOy và xAy’. Chứng tỏ rằng Ot//At’.

Câu 2: Cho $xOy = {120^0}$ và $Ot$ là tia phân giác của góc đó. Trên tia Oy lấy điểm A, qua A vẽ đường thẳng At’ // Ot.

a. Tính góc yAt’

b. Từ A dựng đường thẳng Ax’ song song với Ox. So sánh hai góc t’Ax’ và tOx.

Câu 1: Tìm câu trả lơi sai. Nếu a // b thì: 

A. $\widehat {{A_2}} = \widehat {{B_2}}$

B. $\widehat {{A_2}} = \widehat {{B_1}}$

C. $\widehat {{A_1}} + \widehat {{B_3}} = {180^o}$

D. $\widehat {{A_4}} + \widehat {{B_4}} = {180^o}$

Câu 2: Cho hình vẽ, biết AB // CD 

Tính số đo $\widehat A,\widehat B$

A. $\widehat A = {105^o},\,\,\widehat B = {130^o}$

B. $\widehat A = {115^o},\,\,\widehat B = {130^o}$

C. $\widehat A = {115^o},\,\,\widehat B = {150^o}$

D. $\widehat A = {135^o},\,\,\widehat B = {115^o}$

Câu 3: Cho hình vẽ, biết a // b. 

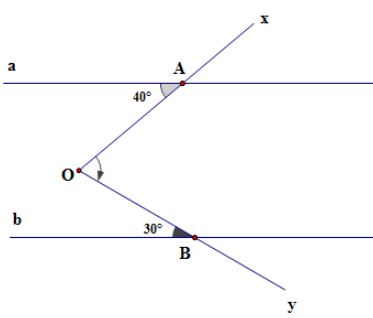
Số đo của góc AOB là:

A. 50^o

B. 70^o

C. 90^o

D. 120^o

Câu 4: Cho hình vẽ sau, biết x // y và $\widehat {{M_1}} = {55^o}$. Tính số đo $\widehat {{N_1}}$

A. 55^o

B. 35^o

C. 60^o

D. 125^o

Qua bài học này, các em cần nắm được những nội dung sau:

• Nắm được tiên đề Ơ-clit về đường thẳng song song.

• Dấu hiệu nhận biết hai đường thẳng song song.