Toán 11 Chương 2 Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian

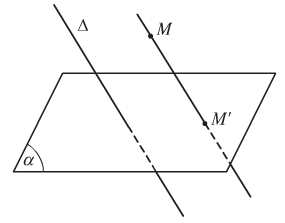
- Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Với mỗi điểm M trong không gian, đường thẳng đi qua M và song song hoặc trùng với \(\Delta \) sẽ cắt \(\left( \alpha \right)\) tại điểm M’ xác định.

- Điểm M’ được gọi là hình chiếu song song của điểm M trên mặt phẳng \(\left( \alpha \right)\) theo phương \(\Delta \).

- Mặt phẳng \(\left( \alpha \right)\) gọi là mặt phẳng chiếu. Phương \(\Delta \) gọi là phương chiếu.

- Phép đặt tương ứng mỗi điểm M trong không gian với hình chiếu M’ của nó trên mặt phẳng \(\left( \alpha \right)\) được gọi là phép chiếu song song lên \(\left( \alpha \right)\) theo phương \(\Delta \).

- Chú ý: Nếu một đường thẳng có phương trùng với phương chiếu thì hình chiếu của đường thẳng đó là một điểm.

- Định lí 1:

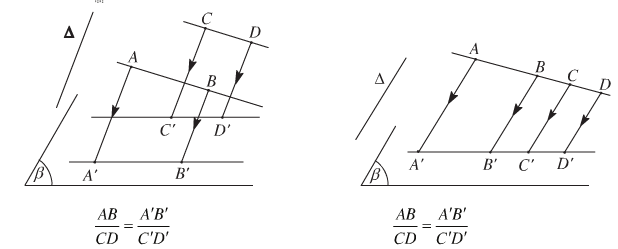
+ Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.

+ Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thành đoạn thẳng.

+ Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.

+ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.

- Hình biểu diễn của một hình H trong không gian là hình chiếu song song của hình H trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.

- Hình biểu diễn của các hình thường gặp

+ Tam giác: Một tam giác bất kì bao giờ cũng có thể coi là hình biểu diễn của một tam giác có dạng tùy ý cho trước (có thể là tam giác đều, tam giác cân, tam giác vuông,…).

+ Hình bình hành: Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành có dạng tùy ý cho trước (có thể là hình bình hành, hình vuông, hình thoi, hình chữ nhật,…).

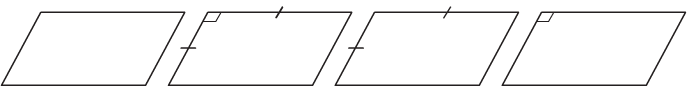
+ Hình thang: Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình thang có dạng tùy ý cho trước, miễn là tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình thang ban đầu.

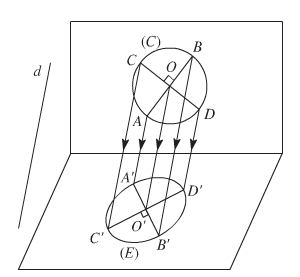
+ Hình tròn: dùng hình elip để biểu diễn cho hình tròn.

Bài 1: Cho hình chóp S.ABC có các mặt bên là tam giác đều. Gọi M là trung điểm của BC, N là điểm trên cạnh SA sao cho \(\frac{{SN}}{{NA}} = \frac{1}{2}\). Tìm hình chiếu của N qua phép chiếu song song phương SM mặt phẳng chiếu (ABC).

Hướng dẫn giải:

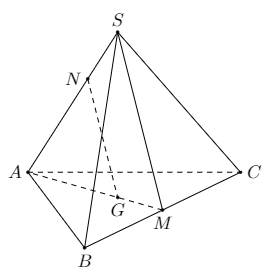
Ta có các tam giác SAB, SAC, SBC là các tam giác đều. Suy ra tam giác ABC cũng là tam giác đều.

Gọi G là trọng tâm tam giác ABC.

Ta có \(\frac{{SN}}{{NA}} = \frac{{MG}}{{GA}} = \frac{1}{2} \Rightarrow \) NG // SM.

Vậy G là hình chiếu song song theo phương SM của N trên (ABC).

Bài 2: Cho hình lăng trụ ABC.A’B’C’. Gọi G là trọng tâm của tam giác ABC. Qua phép chiếu song song phương AA’ mặt phẳng chiếu (A’B’C’) biến G thành G’. Chứng minh G’ là trọng tâm của tam giác A’B’C’.

Hướng dẫn giải:

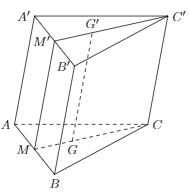
Gọi M là trung điểm của AB.

Phép chiếu song song phương AA’ biến C thành C’, biến M thành M’.

Ta có G là trọng tâm tam giác ABC. Suy ra C, M, G thẳng hàng và \(\frac{{CG}}{{CM}} = \frac{2}{3}\).

Do đó C’, G’, M’ thẳng hàng và \(\frac{{C'G'}}{{C'M'}} = \frac{2}{3}\).

Mặt khác M là trung điểm của AC nên M’ là trung điểm của A’B’.

Vậy G’ là trọng tâm tam giác A’B’C’.

 Bài 1: Cho hình hộp ABCD.A’B’C’D’, tìm ảnh của điểm C, D’.

a) Qua phép chiếu song song phương AB mặt phẳng chiếu (BCC’B’).

b) Qua phép chiếu song song phương A’B mặt phẳng chiếu (CDD’C’).

Bài 2: Cho hình chóp S.ABCD có đáy là hình bình hành, O là tâm của đáy. Trên cạnh SB, SD lần lượt lấy điểm M, N sao cho SB = 3MB, ND = 2 SN. Hình chiếu của M, N qua phép chiếu song song phương SO mặt phẳng chiếu (ABCD) lần lượt là P, Q. Tính tỉ số \(\frac{{BP}}{{QD}}\).

Bài 3: Cho hình chóp S.ABCD, đáy là hình bình hành. Gọi O là tâm của đáy, lấy M, N lần lượt là ảnh của điểm A, D qua phép chiếu song song phương SO trên mặt phẳng (SBC). Khi đó tứ giác BCNM là hình gì? Hình chóp S.ABCD thêm điều kiện gì để tứ giác BCNM là hình vuông?

Bài 1: Giả sử tam giác ABC là hình biểu diễn một tam giác đều. Hình biểu diễn của tâm đường tròn ngoại tiếp tam giác đều là:

A. Giao điểm của hai đường trung tuyến của tam giác ABC.

B. Giao điểm của hai đường trung trực của tam giác ABC.

C. Giao điểm của hai đường cao của tam giác ABC.

D. Giao điểm của hai đường phân giác của tam giác ABC.

Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn CD. Mặt phẳng nào sau đây có thể làm mặt phẳng chiếu trong phép chiếu song song theo phương CD?

A. (SCD).

B. (ABCD).

C. (SAB).

D. (SBD).

Bài 3: Cho hình lăng trụ ABC.A’B’C’, qua phép chiếu song song phương AA’, mặt phẳng chiếu (ABC) biến I thành I’. Trong đó I là trung điểm của A’C’. Chọn mệnh đề đúng?

A. I’ là trung điểm của AB.

B. I’ là trung điểm của AC.

C. I’ là trung điểm của BC.

D. Cả ba đáp án trên đều sai.

Bài 4: Cho hình chóp S.ABCD có đáy là hình bình hành, trên cạnh SA lấy điểm M sao cho \(MA=3MS\). Gọi O là tâm của đáy, qua phép chiếu song song phương MO mặt phẳng chiếu (ABCD) biến điểm S thành điểm N. Tính tỉ số \(\frac{{CN}}{{CA}}\).

A. \(\frac{1}{3}\).

B. \(\frac{3}{4}\).

C. \(\frac{1}{6}\).

D. \(\frac{2}{3}\).

Bài 5: Cho tứ diện ABCD và M là điểm bất kì thuộc miền trong tam giác BCD. Gọi B’, C’, D’ lần lượt là hình chiếu song song của M theo các phương AB, AC, AD lên các mặt (ACD), (ABD), (ABC). Tính \(\frac{{MB'}}{{AB}} + \frac{{MC'}}{{AC}} + \frac{{MD'}}{{AD}}\)?

A. \(\frac{1}{9}\).

B. \(\frac{1}{3}\).

C. 1.

D. 3.

Qua bài học này các em cần nắm được những nội dung sau:

- Khái niệm phép chiếu song song; khái niệm hình biểu diễn của một hình không gian.

- Xác định được: phương chiếu, mặt phẳng chiếu trong một phép chiếu song song. Dựng được ảnh của một điểm, một đoạn thẳng, một tam giác, một đường tròn qua một phép chiếu song song.