Toán 8 Chương 2 Bài 5: Diện tích hình thoi

Diện tích của một tứ giác có hai đường chéo vuông góc bằng nửa tích độ dài hai đường chéo đó.

\({S_{ABCD}}=\dfrac{1}{2} AC. BD\)

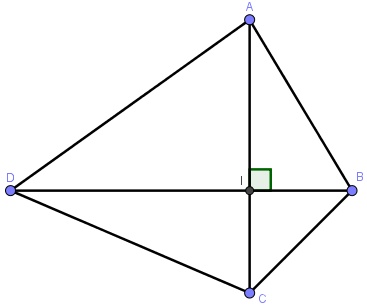
Nhận xét: Diện tích của một tứ giác có hai đường chéo vuông góc bằng một nửa tích hai đường chéo. 

Diện tích hình thoi bằng nửa tích độ dài hai đường chéo.

\(S=\dfrac{1}{2}{d_1}.{d_2}\)

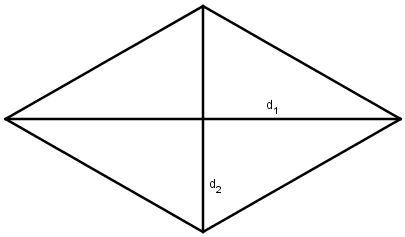
- Lưu ý: Hình thoi cũng là một hình bình hành đặc biệt nên ta có thể sử dụng công thức tính diện tích hình bình hành để tính diện tích hình thoi.

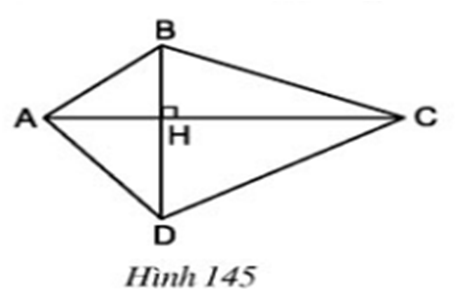
Hãy tính diện tích tứ giác \(ABCD\) theo \(AC, BD\), biết \(AC ⊥ BD\) tại \(H\) (h.\(145\))

Hướng dẫn giải

\({S_{ABC}} = \dfrac{1}{2}BH.AC\)

\({S_{ADC}}=\dfrac{1}{2}DH.AC\)

\({S_{ABCD}} = {S_{ABC}} + {S_{ADC}}\)\( \,= \dfrac{1}{2}BH.AC + \dfrac{1}{2}DH.AC\)\(\, = \dfrac{1}{2}(BH + DH).AC = \dfrac{1}{2}BD.AC\)

a) Hãy vẽ một tứ giác có độ dài hai đường chéo là \(3,6cm; 6cm\) và hai đường chéo đó vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy? Hãy tính diện tích mỗi tứ giác vừa vẽ?

b) Hãy tính diện tích hình vuông có độ dài đường chéo là \(d\).

Hướng dẫn giải

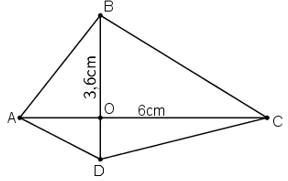
a) Học sinh tự vẽ tứ giác thỏa mãn điều kiện đề bài, chẳng hạn như tứ giác \(ABCD\) ở hình vẽ có:

\(AC = 6cm\)

\(BD = 3,6cm\)

\(AC \perp BD\)

Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài.

Diện tích của tứ giác vừa vẽ là:

 \(S_{ABCD}= \dfrac{1}{2} AC. BD = \dfrac{1}{2}6. 3,6 = 10,8\) (\(cm^2\))

b) Diện tích hình vuông có độ dài đường chéo là \(d\)

Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, nên diện tích là:

\(S = \dfrac{1}{2} d.d = \dfrac{1}{2} d^2\)

Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi.

Hướng dẫn giải

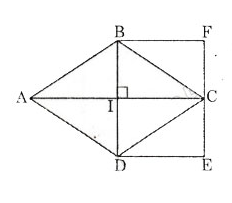
Cho hình thoi \(ABCD\) có hai đường chéo cắt nhau tại \(I\). Suy ra \(I\) là trung điểm \(AC\) hay \(IC=\dfrac{1}{2}\) \(AC\)  (tính chất)

Vẽ hình chữ nhật có một cạnh là đường chéo \(BD\), cạnh kia bằng \(IC\) ( \(IC=\dfrac{1}{2}\) \(AC\))

Khi đó diện tích của hình chữ nhật \(BFED\) bằng diện tích hình thoi \(ABCD\).

Thật vậy:

\({S_{BF{\rm{ED}}}} = BD.IC = B{\rm{D}}.\dfrac{1}{2}AC \)\(= \dfrac{1}{2}B{\rm{D}}.AC = {S_{ABC{\rm{D}}}}.\)

Từ đó suy ra cách tính diện tích hình thoi: Diện tích hình thoi bằng nửa tích hai đường chéo.

Câu 1: Trong những hình thoi có chu vi bằng nhau, hãy tìm hình thoi có diện tích lớn nhất.

Câu 2: Tính diện tích hình thoi, biết cạnh của nó dài \(6,2\,cm\) và một trong các góc của nó có số đo bằng \(30°\)

Câu 3: Cho hình thoi \(ABCD,\) biết \(AB = 5cm,\, AI = 3cm\) (\(I\) là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi đó.

Câu 4: 

a) Hãy vẽ một tứ giác có hai đường chéo vuông góc với nhau, biết độ dài hai đường chéo đó là \(a\) và \(\dfrac{1}{2}a\). Hỏi có thể vẽ được bao nhiêu hình như vậy ?

b) Có thể vẽ được mấy hình thoi, biết độ dài hai đường chéo là \(a\) và \(\dfrac{1}{2}a\) ?

c) Hãy tính diện tích các hình vừa vẽ.

Câu 1: Hai đường chéo hình thoi có độ dài là 6cm và 8cm. Độ dài cạnh hình thoi là:

A. 6 cm

B. 5 cm

C. 3 cm

D. 4 cm

Câu 2: Cho hình thoi MNPQ. Biết A, B, C, D lần lượt là các trung điểm của các cạnh NM, NP, PQ, QM. Tính tỉ số diện tích tứ giác ABCD và hình thoi MNPQ

A. \(\frac{1}{2}\)

B. \(\frac{2}{3}\)

C. 2

D. \(\frac{1}{3}\)

Câu 3: Hình thoi có đọ dài hai đường chéo là 6cm và 8cm. Tính độ dài đường cao của hình thoi 

A. 9,6 cm

B. 4,8 cm

C. 3,6 cm

D. 5,4 cm

Câu 4: Cho hình bình hành ABCD có AB = BC = 10 cm và O là giao điểm của hai đường chéo sao cho OA = 6cm. Tính diện tích hình bình hành ABCD

A. 96    

B. 80

C. 72    

D. 64

Câu 5: Cho hình thoi ABCD có diện tích là 24cm2. Tỉ số độ dài hai đường chéo là 3: 4. Tính độ dài hai đường chéo của hình thoi

A. 9cm và 12cm    

B. 12cm và 16cm

C. 6cm và 8cm    

D. 3cm và 4cm

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm được công thức tính diện tích hình thoi
• Biết được hai cách tính diện tích hình thoi, biết cách tính diện tích của một tứ giác có hai đường chéo vuông góc.
• Vẽ được hình thoi một cách chính xác và phát hiện và chứng minh được định lí về diện tích hình thoi.