Toán 6 Chương 2 Bài 4: Khi nào góc xOy + góc yOz= góc xOz?

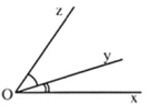
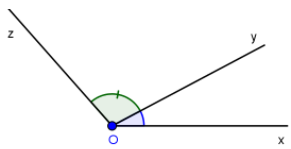
Nếu tia Oy nằm giữa hai tia Ox và Oz thì \(\widehat {xOy}\,\, + \,\widehat {yOz\,}\, = \,\widehat {xOz}\)

Ngược lại, nếu \(\widehat {xOy}\,\, + \,\widehat {yOz\,}\, = \,\widehat {xOz}\) thì tia Oy nằm giữa hai tia Ox, Oz.

- Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh nhau.

Ví dụ: \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề nhau, cạnh chung là Oy.

- Hai góc phụ nhau là hai góc có tổng số đo bẳng \({90^0}\)

Ví dụ: góc \({35^0}\) và góc \({55^0}\) là hai góc phụ nhau vì \({35^0} +{55^0}=90^0\).

- Hai góc bù nhau là hai góc có tổng số đo bẳng \({180^0}\)

Ví dụ: \({115^0}\) và góc \({65^0}\) là hai góc bù nhau vì \({115^0}+{65^0}=180^0\)

- Hai góc lề bù là hai góc vừa kề nhau, vừa bù nhau.

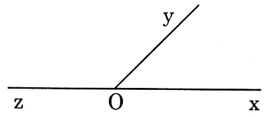
Ví dụ: Hai góc xOy và yOz trên hình vẽ vẽ là hai góc kề bù vì có cạnh Oy chung và hai cạnh Ox và Oz là hai tia đối nhau.

Câu 1: Gọi Oz là tia nằm giữa hai tia Ox, Oy. Biết \(\widehat {xOy}\, = \,{a^0},\,\widehat {zOx}\, = \,{b^0}.\) Tính \(\widehat {yOz}\)?

Hướng dẫn giải

\(\widehat {yOz} = \widehat {xOy} - \widehat {zOx}\, = \,{a^0}\, - \,{b^0}.\)

Câu 2: Cho hình

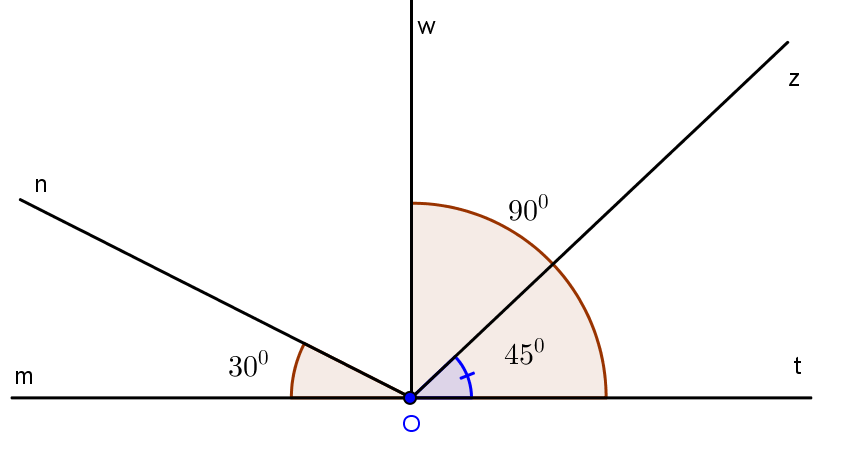
a) Gọi tên các cặp góc kề nhau đỉnh O trong hình đó.

b) Cho biết số đo của các góc đỉnh O trong hình đó.

c) Cho biết những cặp góc phụ nhau đỉnh O

d) Cho biết những cặp góc bù nhau đỉnh O.

Hướng dẫn giải

a) Các cặp góc kề nhau đỉnh O là: \(\widehat {mOn}\) và \(\widehat {nOw}\); \(\widehat {mOn}\) và \(\widehat {nOz}\); \(\widehat {mOn}\) và \(\widehat {nOt}\); \(\widehat {mOw}\) và \(\widehat {zOw}\); \(\widehat {mOw}\) và \(\widehat {tOw}\); \(\widehat {mOz}\) và \(\widehat {zOt}\); \(\widehat {wOn}\) và \(\widehat {zOw}\); \(\widehat {wOn}\) và \(\widehat {tOw}\); \(\widehat {wOz}\) và \(\widehat {zOt}\).

b) \(\widehat {mOt} = {180^0};\,\widehat {mO{\rm{w}}}\, = {90^0};\,\widehat {nO{\rm{w}}}\, = {60^0};\,\widehat {{\rm{w}}Oz} = {45^0}\)

c) \(\widehat {mOn}\) và \(\widehat {nOw}\); \(\widehat {wOz}\) và \(\widehat {zOt}\)

d) \(\widehat {mOn}\) và \(\widehat {nOt}\); \(\widehat {wOm}\) và \(\widehat {wOt}\); \(\widehat {mOz}\) và \(\widehat {zOt}\)

Câu 1:  Ở hình, hai tia OI, OK đối nhau. Tia OI cắt đoạn thẳng AB tại I. Biết \(\widehat {KOA}\, = \,\,{120^0},\,\widehat {BOI}\, = \,{45^0}.\) Tính \(\widehat {KOB},\,\widehat {AOI},\,\widehat {BOA}.\)

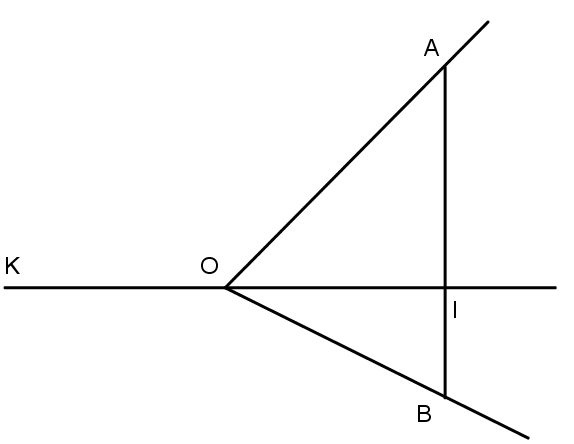
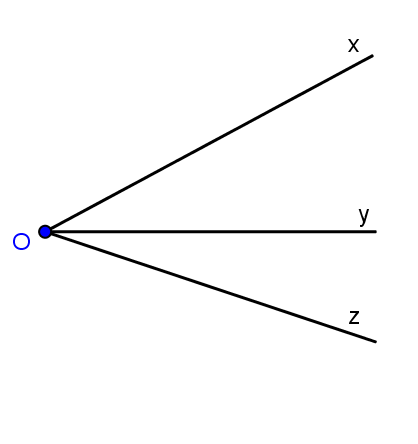
Câu 2:  Xem hình, làm thế nào để chỉ đo hai góc mà biết được số đo của cả ba góc \(\widehat {xOy}\), \(\widehat {xOz}\), \(\widehat {yOz}\)?

Câu 3: Trên đường thẳng d từ trái sang phải ta lấy các điểm A, D, C, B và lấy điểm  O nằm ngoài đường thẳng d. Biết \(\widehat {AOD} = {30^0},\,\widehat {DOC} = {40^0},\,\widehat {AOB}\, = \,{90^0}.\) Tính \(\widehat {AOC},\,\widehat {COB}.\)

Câu 1: Hai góc kề bù là hai góc:

A. Có tổng số đo là 180⁰

B. Có chung một tia và có tổng số đo là 180⁰

C. Kề nhau và có tổng số đo là 180⁰

D. Có chung một cạnh và có tổng số đo là 180⁰

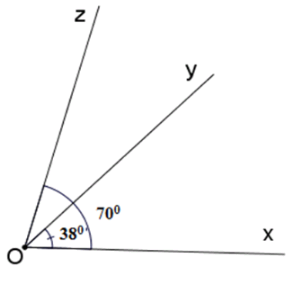
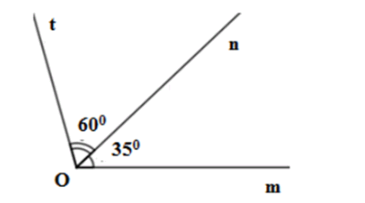
Câu 2: Tính góc yOz trên hình vẽ:

A. 32⁰

B. 70⁰

C. 38⁰

D. 60⁰

Câu 3: Cho góc A và góc B là hai góc phụ nhau và chúng có số đo bằng nhau. Tính số đo mỗi góc

A. \(\widehat A = {30^0},\widehat B = {60^0}\)

B. \(\widehat A = \widehat B = {40^0}\)

C. \(\widehat A = \widehat B = {45^0}\)

D. \(\widehat A = \widehat B = {55^0}\)

Câu 4: Cho góc xOy và góc yOy' là hai góc kề bù. Biết \(\widehat {xOy} = {80^0}\), số đo của góc yOy' là:

A. 100⁰

B. 70⁰

C. 80⁰

D. 60⁰

Câu 5: Cho hình vẽ, biết tia On nằm giữa hai tia Ot và Om

Số đo của góc tOm là:

A. 105⁰

B. 100⁰

C. 115⁰

D. 95⁰

Qua bài học này, các em cần nắm được những nội dung chính sau:

• Nhận biết được cặp góc kề nhau, phụ nhau, bù nhau, kề bù.
• Biết vận dụng hệ thức để giải các bài toán tìm góc chưa biết dạng đơn giản.