Toán 7 Chương 1 Bài 4: Hai đường thẳng song song
Ở lớp 6 các em đã được học về khái niệm hai đường thẳng song song. Bài học hôm nay sẽ cung cấp thêm kiến thức về dấu hiện nhận biết hai đường thẳng song song. Qua hệ thống kiến thức và bài tập minh họa có hướng dẫn chi tiết dưới đây sẽ giúp các em nắm được nội dung bài học và dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

Toán 7 Chương 1 Bài 4: Hai đường thẳng song song
1. Tóm tắt lý thuyết
1.1. Nhắc lại kiến thức lớp 6
- Hai đường thẳng song dong là hai đường thẳng không có điểm chung.
- Hai đường thẳng phân biệt thì hoặc cắt nhau hoặc song song.
1.2. Dấu hiệu nhận biết hai đường thẳng song song
- Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.
- Ký hiệu: a // b
- Ta còn nói đường thẳng a song song với đường thẳng b, hoặc đường thẳng b song song với đường thẳng a.
.jpg)
Ví dụ: Hình vẽ trên ta có đường thẳng a song song với đường thẳng b vì có một cặp góc so le trong bằng nhau ( bằng 45 độ).
1.3. Cách vẽ hai đường thẳng song song
- Dùng góc nhọn 60o60o của êke để vẽ hai góc so le trong bằng nhau:
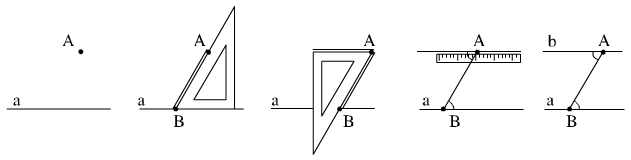
- Dùng góc nhọn 60o60o của êke để vẽ hai góc đồng vị bằng nhau:
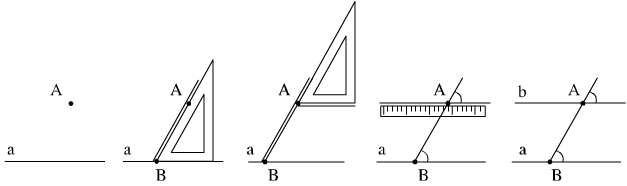
2. Bài tập minh họa
Câu 1:
a. Nêu các ví trí tương đối của hai đường thẳng phân biệt. Hai đường thẳng ấy có thể chia mặt phẳng thành bao nhiêu phần?
b. Cũng hỏi tương tự đối với ba đường thẳng phân biệt.
Hướng dẫn giải:
.jpg)
a. Hai đường thẳng song song chia mặt phẳng thành ba phần (hình a)
Hai đường thẳng cắt nhau chia mặt phẳng thành bốn phần (hình b)
b. Ba đường thẳng song song với nhau chia mặt phẳng thành 4 phần (hình c)
Ba đường thẳng song song bị cắt bởi đường thẳng thứ ba chia mặt phẳng thành 6 phần (hình d)
Ba đường thẳng cắt nhau tại một điểm: mặt phẳng được chia thành 6 phần (hình e)
Ba đường thẳng cắt nhau từng đôi một tại các điểm khác nhau chia mặt phẳng thành 7 phần (hình g)
Câu 2: Cho ^xOy=α,ˆxOy=α, điểm A nằm trên tia Oy. Qua A vẽ tia Am. Tính số đo của góc OAm để AM song song với Ox.
Hướng dẫn giải
.jpg)
Xét hai trường hợp:
a. Nếu tia Am thuộc miền trong góc xOy:
Để Am//Ox thì phải có ^A1=αˆA1=α (đồng vị)
Mà ^A1+^A2=1800ˆA1+ˆA2=1800 (hai góc kề bù)
Nên ^A2=1800−^A1=1800−αˆA2=1800−ˆA1=1800−α
Vậy ^OAm=1800−αˆOAm=1800−α
b. Nếu tia Am thuộc miền ngoài góc xOy:
Để Am//Ox thì phải có ^A1=αˆA1=α (so le trong)
Vậy ^OAm=αˆOAm=α
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho hình vẽ bên, trong đó ^AOB=600,ˆAOB=600, Ot là tia phân giác của góc AOB. Hỏi các tia Ax, Ot và By có song song với nhau không? Vì sao?
.jpg)
Câu 2: Cho hai đường x’x và y’y, điểm A trên tia x’x và điểm B trên y’y sao cho hai tia Ax và By cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng AB. Cho biết: x′AB+yBA+BAx=2160 và BAx=4x′AB. Chứng minh rằng: x’x //y’y.
Câu 3: Cho hai góc xOy có số đo bằng 300 và điểm A nằm trên cạnh Ox. Dựng tia Az song song với tia Oy và nằm trong góc xOy.
a. Tìm số đo góc OAz.
b. Gọi Ou và Av theo thứ tự là các tia phân giác của các góc xOy và xAz. Chứng tỏ rằng Ou song song với Av.
3.2. Bài tập trắc nghiệm
Câu 1: Trong số các câu sau có bao nhiêu câu đúng?
Nếu một đường thẳng cắt hai đường thẳng song song thì:
(I) Hai góc đồng vị bằng nhau.
(II) Hai góc so le ngoài bằng nhau.
(III) Hai góc trong cùng phía bù nhau.
(IV) Hai góc so le trong bằng nhau.
A. 1.
B. 2.
C. 3.
D. 4.
Câu 2: Vẽ một đường thẳng cắt hai đường thẳng.Trong các góc tạo thành có một cặp góc đồng vị bằng nhau. Khi đó, mỗi cặp góc trong cùng phía?
A. bằng nhau.
B. bù nhau.
C. đối nhau.
D. không có đáp án đúng .
Câu 3: Điền vào chỗ trống: "Nếu hai đường thẳng d, d' cắt đường thẳng xy tạo thành một cặp góc trong cùng phía...thì d//d'
A. bù nhau.
B. bằng nhau.
C. phụ nhau.
D. kề nhau .
Câu 4: Chọn câu đúng:
A. Qua điểm A nằm ngoài đường thẳng m, có vô số đường thẳng song song với m.
B. Qua điểm A nằm ngoài đường thẳng m. có duy nhất một đường thẳng song song với m.
C. Qua điểm A nằm ngoài đường thẳng d, có hai đường thẳng phân biệt cùng song song với d.
D. Nếu hai đường thẳng AB và AC cùng song song với đường thẳng d thì hai đường thẳng AB và AC song song với nhau.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Dấu hiệu nhận biết hai đường thẳng song song.
- Dùng êke để vẽ đường thẳng song song với một đường thẳng cho trước đi qau một điểm cho trước nằm ngoài đường thẳng đó (hai cách vẽ).
- Làm các bài toán có liên quan: chứng minh hai đường thẳng song song , tính góc dựa trên giả thiết hai đường thẳng song song.
Tham khảo thêm
- doc Toán 7 Chương 1 Bài 1: Hai góc đối đỉnh
- doc Toán 7 Chương 1 Bài 2: Hai đường thẳng vuông góc
- doc Toán 7 Chương 1 Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- doc Toán 7 Chương 1 Bài 5: Tiên đề Ơ-clit về đường thẳng song song
- doc Toán 7 Chương 1 Bài 6: Từ vuông góc đến song song
- doc Toán 7 Chương 1 Bài 7: Định lí




