Toán 10 Chương 1 Bài 4: Các tập hợp số

- Tập hợp số tự nhiên: \(\mathbb{N} = \left\{ {0,1,2,3,4,...} \right\}.\) \(\mathbb{N}^*\) là tập hợp các số tự nhiên khác 0.

- Tập hợp các số nguyên: \(\mathbb{Z} = \left\{ {..., - 2, - 1,0,1,2,...} \right\}.\)

- Tập hợp các số hữu tỉ: \(Q = \left\{ {x = \frac{m}{n},m\,,n \in \mathbb{Z},n \ne 0} \right\}.\)

- Tập hợp số thực: \(\mathbb{R}.\)

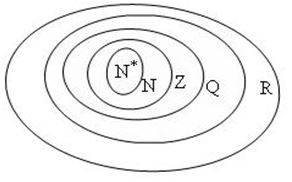
- Ta có: \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}.\)

Biểu đồ Ven các tập hợp số:

a) Khoảng

\((a;b) = \left\{ {x \in \mathbb{R}/a < x < b} \right\}\)

\(\left( {a; + \infty } \right) = \left\{ {x \in \mathbb{R}/x > a} \right\}\)

\(\left( { - \infty ;b} \right) = \left\{ {x \in \mathbb{R}/x < b} \right\}\)

b) Đoạn

\({\rm{[}}a;b{\rm{]}} = \left\{ {x \in \mathbb{R}/a \le x \le b} \right\}\)

c) Nửa khoảng

\(\left[ {a;b} \right) = \left\{ {x \in \mathbb{R}/a \le x < b} \right\}\)

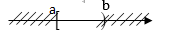
\(\left( {a;b} \right] = \left\{ {x \in \mathbb{R}/a \le x < b} \right\}\)

\(\left[ {a; + \infty } \right) = \left\{ {x \in \mathbb{R}/x \ge a} \right\}\)

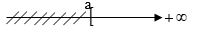
\(\left( { - \infty ;b} \right] = \left\{ {x \in \mathbb{R}/x \le b} \right\}\)

d) Kí hiệu

\( + \infty :\) Dương vô cực (Hoặc dương vô cùng).

\( - \infty :\) Âm vô cực (Hoặc âm vô cùng).

Tập \(\mathbb{R}\) có thể viết \(\mathbb{R} = \left( { - \infty ; + \infty } \right).\) Gọi là khoảng \(\left( { - \infty ; + \infty } \right).\)

Câu 1: Xác định các tập hợp sau và biểu diễn chúng trên trục số:

a) \(\left[ { - 2;4} \right) \cup \left( {-3;1} \right];\)

b) \(\left( { - 2; 9} \right) \cup \left( {8; + \infty } \right);\)

c) \(\left[ { - 9;3} \right) \cap \left( { - 1;15} \right];\)

Hướng dẫn giải

a) \(\left[ { - 2;4} \right) \cup \left( {-3;1} \right] = \left[ { - 3;4} \right].\)

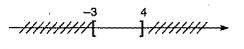
b) \(\left( { - 2; 9} \right) \cup \left( {8; + \infty } \right) = ( - 2; + \infty ).\)

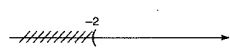
c) \(\left[ { - 9;3} \right) \cap \left( { - 1;15} \right] = {\rm{[}} - 1;3].\)

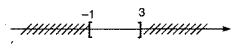
Câu 2: Tìm giá trị lớn nhất của m sao cho \(\left( {m+1;m+13} \right) \subset \left( { - 5;5} \right).\)

Hướng dẫn giải

\(\left( {m + 1;m +5} \right) \subset \left( { - 5;5} \right)\) khi và chỉ khi: \(\left\{ \begin{array}{l}m +1 \ge  -5\\m+12 \le 5\end{array} \right. \Leftrightarrow m = -6.\)

Câu 1: Cho 2 tập hợp \(A = \left\{ {2;4;6;8} \right\};B = \left\{ {4;8;9;0} \right\}\). Xét các khẳng định sau đây:

\(A \cap B = \left\{ {4;8} \right\}\)

\(A \cup B = \left\{ {0;2;4;6;8;9} \right\}\)

\(B\backslash A = \left\{ {2;6} \right\}\). 

Có bao nhiêu khẳng định đúng trong các khẳng định trên?

A. 0

B. 1

C. 2

D. 3

Câu 2: Tập hợp \(\left[ { - 3;1} \right) \cap \left[ {0;4} \right]\) bằng tập hợp nào sau đây?

A. \(\left( {0;1} \right)\)

B. \(\left[ {0;1} \right)\)

C. . \(\left( {0;1} \right]\)

D. \(\left[ {0;1} \right]\) 

Câu 3: Tập hợp \(\left( { - 2;3} \right)\backslash \left[ {1;5} \right]\) bằng tập hợp nào sau đây?

A. \(\left( { - 2;1} \right)\)

B. \(\left( { - 2;1} \right]\)

C. \(\left( { - 3; - 2} \right)\)

D. \(\left( { - 2;5} \right)\)

Câu 4: Cho \(M = \left[ { - 4;7} \right]\) và \(N = \left( { - \infty ; - 2} \right) \cup \left( {3; + \infty } \right).\) Tìm tập hợp \(M \cap N.\)

A. \(\left[ { - 4; - 2} \right]\)

B. \(\left( {3;7} \right]\)

C. \(\left[ { - 4; - 2} \right) \cup \left( {3;7} \right]\)

D. \(\left[ { - 4;2} \right) \cap \left( {3;7} \right]\)

Câu 5: Cho số thực \(a < 0.\) Điều kiện cần và đủ để hai tập \(A = \left( { - \infty ;9a} \right)\) và \(B = \left( {\frac{4}{a}; + \infty } \right)\) có giao khác rỗng là:

A. \( - \frac{2}{3} < a < 0\)

B. \( - \frac{2}{3} \le a < 0\)

C. \( - \frac{3}{4} < a < 0\)

D. \( - \frac{3}{4} \le a < 0\)