Toán 11 Chương 3 Bài 3: Đường thẳng vuông góc với mặt phẳng

Đường thẳng d được gọi là vuông góc với mặt phẳng \((\alpha)\) nếu d vuông góc với mọi đường thẳng a nằm trong mặt phẳng \((\alpha)\).

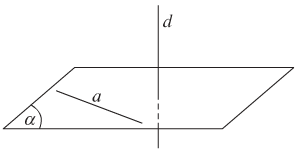
Kí hiệu: \(d \bot \left( \alpha \right)\).

- Định lí: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

- Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba.

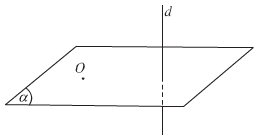
- Tính chất 1: Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

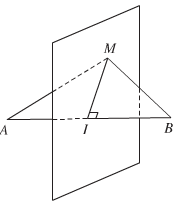
+ Mặt phẳng trung trực của một đoạn thẳng:

Mặt phẳng đi qua trung điểm I của đoạn thẳng AB và vuông góc với đường thẳng AB là mặt phẳng trung trực của đoạn thẳng AB.

- Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm và vuông góc với một mặt phẳng cho trước.

- Tính chất 1:

+ Mặt phẳng nào vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng còn lại.

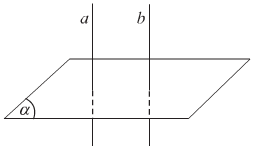
+ Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

- Tính chất 2:

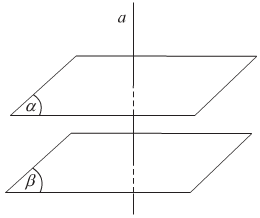
+ Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

+ Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

- Tính chất 3:

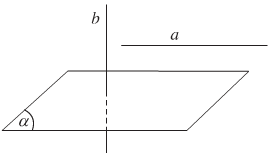
+ Cho đường thẳng a và mặt phẳng \((​\alpha)\) song song với nhau. Đường thẳng nào vuông góc với \((​\alpha)\) thì cũng vuông góc với a.

+ Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.

a) Phép chiếu vuông góc

Cho đường thẳng \(\Delta \) vuông góc với mặt phẳng \((​\alpha)\). Phép chiếu song song theo phương của \(\Delta \) lên mặt phẳng \((​\alpha)\)  được gọi là phép chiếu vuông góc lên mặt phẳng \((​\alpha)\).

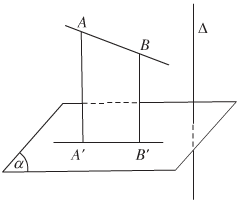
b) Định lí ba đường vuông góc

Cho đường thẳng a nằm trong mặt phẳng \((​\alpha)\) và b là đường thẳng không thuộc \((​\alpha)\) đồng thời không vuông góc với \((​\alpha)\). Gọi b' là hình chiếu vuông góc của b trên \((​\alpha)\). Khi đó a vuông góc với b khi và chỉ khi a vuông góc với b'.

c) Góc giữa đường thẳng và mặt phẳng

- Định nghĩa: 

Cho đường thẳng d và mặt phẳng \((​\alpha)\).

Trường hợp đường thẳng d vuông góc với mặt phẳng \((​\alpha)\) thì ta nói rằng góc giữa đường thẳng d và mặt phẳng \((​\alpha)\) bằng \(90^o\).

Trường hợp đường thẳng d không vuông góc với mặt phẳng \((\alpha)\) thì góc giữa d và hình chiếu d' của nó trên \((​\alpha)\) gọi là góc giữa đường thẳng d và mặt phẳng \((​\alpha)\).

- Chú ý: Nếu \(\varphi \) là góc giữa đường thẳng d và mặt phẳng \((​\alpha)\) thì ta luôn có \({0^o} \le \varphi \le {90^o}\).

Bài 1: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy, \(SA=\frac{{a\sqrt 3 }}{2}\). Gọi K, I là trung điểm của IS, CB. Chứng minh rằng AK \( \bot \) (SBC).

Hướng dẫn giải:

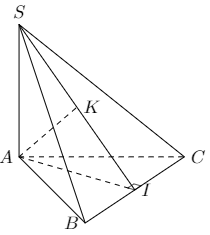
Tam giác ABC có I là trung điểm BC \(\Rightarrow \) AI \( \bot \) BC (1).

Áp dung định lí Py - ta - go vào tam giác ABI ta tính được \(AI=\frac{{a\sqrt 3 }}{2}\).

Lại có SA \( \bot \) (ABC) \(\Rightarrow \) SA \( \bot \) BC (2).

Từ (1) và (2) suy ra BC \( \bot \) (SAI) \(\Rightarrow \) BC \( \bot \) AK (3).

Xét tam giác SAI có \(SA=AI=\frac{{a\sqrt 3 }}{2}\) nên tam giác SAI cân tại A.

Mà K là trung điểm IS nên AK \( \bot \) IS (4).

Từ (3) và (4) suy ra AK \( \bot \) (SBC).

Bài 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = \(a\sqrt 6 \) và SA vuông góc với mặt đáy. Hãy xác định góc giữa:

a) SC và (ABCD).

b) SC và (SAB).

c) SB và (SAC).

d) AC và (SBC).

Hướng dẫn giải:

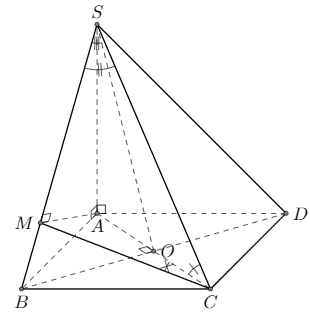
a) Vì AC là hình chiếu vuông góc của SC lên (ABCD) nên góc giữa SC và (ABCD) là góc SCA.

Xét tam giác SCA, ta có:

\(\tan \widehat {SCA} = \frac{{SA}}{{SC}} = \sqrt 3 \).

Vậy (SC, (ABCD)) = \(\widehat {SCA}\) = \(60^o\).

b) Vì BC \( \bot \) (SAB) tại B nên SB là hình chiếu vuông góc của SC lên (SAB).

Do đó (SC, (SAB)) = (SC, SB) = \(\widehat {CSB}\).

Xét tam giác SCB, ta có:

\(\tan \widehat {CSB} = \frac{{BC}}{{SB}} = \frac{a}{{a\sqrt 7 }}=\frac{1}{{\sqrt 7 }}\).

Vậy (SC, (SAB)) = arctan \(\frac{1}{{\sqrt 7 }}\).

c) Vì BO \( \bot \) (SAC) tại O nên SO là hình chiếu vuông góc của SB lên (SAC).

Do đó (SB, (SAC)) = (SB, SO) = \(\widehat {BSO}\).

Xét tam giác SCB, ta có:

\(\sin \widehat {BSO} = \frac{{BO}}{{SB}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{a\sqrt 7 }} = \frac{1}{{\sqrt {14} }}\).

Vậy (SB, (SAC)) = acrsin \( \frac{1}{{\sqrt {14} }}\).

d) Gọi M là hình chiếu vuông góc của A lên SB.

Ta có AM \( \bot \) SB và AM \( \bot \) BC (vì BC \( \bot \) (SAB) và AM \( \subset \) (SAB)).

Nên AM \( \bot \) (SBC) tại M.

Do đó MC là hình chiếu vuông góc của AC lên (SBC). 

Suy ra (AC, (SBC)) = (AC, MC) = \(\widehat {ACM}\).

Xét tam giác SAB, ta có:

\(AM = \frac{{SA.AB}}{{SB}} = \frac{{a\sqrt 6 }}{{\sqrt 7 }}\).

Xét tam giác ACM, ta có:

\(\sin \widehat {ACM} = \frac{{MA}}{{AC}} = \frac{\sqrt {21}}{{7 }}\).

Vậy (AC, (SBC)) = arcsin \(\frac{\sqrt {21}}{{7 }}\).

Bài 1: Cho hình vuông ABCD. Trên đường thẳng vuông góc với (ABCD) tại A ta lấy điểm S bất kì (S khác A). Gọi M, N, P là hình chiếu của điểm A lên SB, SC, SD. Chứng minh rằng:

a) CD \( \bot \) (SAD), BD \( \bot \) (SAC).

b) SC \( \bot \) (AMP).

c) MP \( \bot \) (SAC).

Bài 2: Cho hình chóp S.ABCD có đáy là hinh vuông cạnh a, tâm giác SAB là tam giác đều, tam giác SCD là tam giác vuông tại S. Hai cạnh AB và CD có trung điểm lần lượt là K và H.

a) Tính độ dài các cạnh của tam giác SIJ. Chứng minh SK \( \bot \) (SCD), SH \( \bot \) (SAB).

b) Gọi I là hình chiếu của S trên IJ. Chứng minh SH \( \bot \) AC.

Bài 3: Cho hình chóp S.ABCD có đáy là hình vuông có cạnh bằng a, SA vuông góc với đáy và có độ dài bằng \(a\sqrt 6 \). Tính góc giữa SC với các mặt phẳng sau:

a) (ABCD).

b) (SBA).

c) (SBD).

Bài 4: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SO vuông góc với đáy (O là giao điểm hai đường chéo). Gọi M, N là trung điểm của AS, BC. Biết rằng góc giữa MN và (ABCD) bằng \(60^o\).

a) Tính độ dài cạnh MN và SO.

b) Tính góc giữa MN và (SBD).

Qua bài học này các em cần nắm những nội dung sau:

- Định nghĩa và điều kiện đường thẳng vuông góc với mặt phẳng; khái niệm phép chiếu vuông góc; khái niệm mặt phẳng trung trực của một đoạn thẳng.

- Làm các dạng toán: chứng minh đường thẳng vuông góc với mặt phẳng, đường thẳng vuông góc với đường thẳng; xác định vectơ pháp tuyến của một mặt phẳng; xác định hình chiếu vuông góc của một điểm, một đường thẳng, một tam giác; xác định góc giữa đường thẳng và mặt phẳng.