Toán 8 Chương 2 Bài 3: Diện tích tam giác

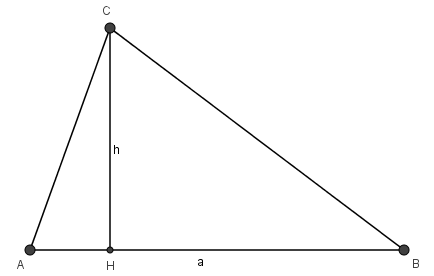
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

\({\rm{S = }}\frac{1}{2}{ah}\)
 

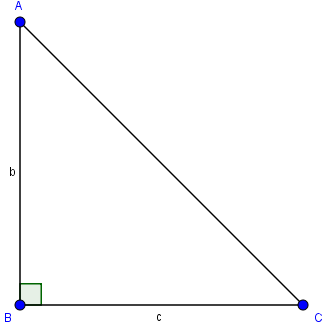
Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông.

\({\rm{S = }}\frac{1}{2}{bc}\)

Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên đường thẳng d cố định song song với BC. Chứng minh rằng tam giác ABC có diện tích không đổi.

Hướng dẫn giải

Đường thẳng d cố định song song với đường thẳng BC cố định nên khoảng cách hai đường thẳng d và BC là không đổi.

Tam giác ABC có cạnh đáy BC không đổi, chiều cao AH là khoảng cách giữa 2 đường thẳng song song không đổi.

Vậy điểm A thay đổi trên đường thẳng d // AB thì diện tích tam giác ABC không đổi.

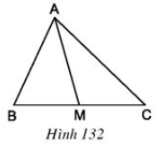
Cho tam giác \(ABC\) và đường trung tuyến \(AM\) (h.\(132\)). Chứng minh rằng:

\({S_{AMB}} = {S_{AMC}}\)

Hướng dẫn giải

Dựng \(AH\) là đường cao của \(\Delta ABC\), khi đó \(\Delta ABM,\Delta AMC\) có chung chiều cao \(AH\).

Ta có:

\({S_{AMB}} = \dfrac{1}{2}BM.AH\) (chiều cao \(AH\) và cạnh đáy \(BM\)) 

\({S_{AMC}} = \dfrac{1}{2}CM.AH\) (chiều cao \(AH\) và cạnh đáy \(CM\)) 

Mà \(BM = CM\) (vì \(AM\) là đường trung tuyến)

Vậy  \({S_{AMB}} = {S_{AMC}}.\)

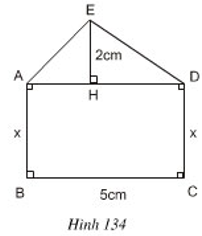
Tính \(x\) sao cho diện tích hình chữ nhật \(ABCD\) gấp \(3\) lần diện tích \(∆ADE\) (h.\(134\))

Hướng dẫn giải

Ta có: \(AD = BC = 5cm\) (vì \(ABCD\) là hình chữ nhật)

Diện tích  \(∆ADE\) là: \({S_{ADE}} = \dfrac{{EH.A{\rm{D}}}}{2} = \dfrac{{2.5}}{2} = 5\;(c{m^2})\)

Diện tích hình chữ nhật \(ABCD\) là: \({S_{ABC{\rm{D}}}} = 5{\rm{x}}\left( {c{m^2}} \right)\)

Theo đề bài ta có: 

\(\begin{array}{l}
{S_{ABC{\rm{D}}}} = 3{S_{ADE}} \\\Rightarrow 5{\rm{x}} = 3.5 = 15\\
\Rightarrow x = 15:5 = 3cm.
\end{array}\) 

Vậy \(x = 3cm.\)

Câu 1: Cho tam giác \(ABC\) có đáy \(BC\) cố định và đỉnh \(A\) di động trên một đường thẳng \(d\) cố định song song với đường thẳng \(BC.\) Chứng minh rằng tam giác \(ABC\) luôn có diện tích không đổi.

Câu 2: Tính diện tích của hình 186 theo các kích thước đã cho trên hình (\(a, b, c\) có cùng đơn vị đo).

Câu 3: Hai cạnh của một tam giác có độ dài là \(5 \,cm\) và \(6\,cm.\) Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau:

a) \(10\) \(c{m^2}\)

b) \(15\) \(c{m^2}\)

c) \(20\) \(c{m^2}\)

Câu 4: Cho tam giác \(ABC,\) biết \(AB = 3AC.\) Tính tỉ số hai đường cao xuất phát từ các đỉnh \(B\) và \(C.\)

Câu 1: Cho tam giác ABC có AB = 6cm, AC = 8cm. Hai đường cao xuất phát từ đỉnh B và C là BH và CK. Biết BH = 9cm. Tính CK

A. 12cm    

B. 15cm

C. 9cm    

D. 8cm