Toán 10 Chương 1 Bài 2: Tổng và hiệu của hai vectơ
Mời các em cùng tham khảo nội dung bài giảng Tổng và hiệu của hai vectơ do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

1. Lí thuyết
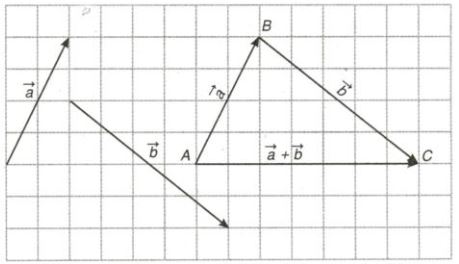
1.1. Định nghĩa tổng của hai vectơ
Định nghĩa:
-
Cho hai vectơ \(\vec a\) và \(\vec b\). Lấy một điểm A nào đó, rồi xác định điểm B và C sao cho \(\vec {AB}=\vec {a}\); \(\vec {BC}=\vec {b}\). Khi đó \(\vec {AC}\) là tổng của hai vectơ \(\vec a\) và \(\vec b\).
-
Ta viết: \(\vec {AC}=\vec{a}+\vec{b}\).
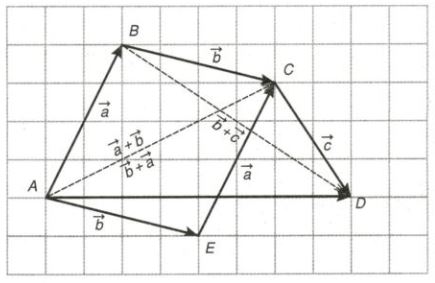
1.2. Tính chất của phép cộng vectơ
Ta có các tính chất sau:
-
Tính chất giao hoán: \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\).
-
Tính chất kết hợp: \((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\).
-
Tính chất vectơ-không \(\vec{a}+\vec{0}=\vec{a}\).
1.3. Quy tắc cần nhớ
a) Quy tắc ba điểm: Với ba điểm A, B, C bất ki, ta luôn có:
\(\vec{AB}+\vec{BC}=\vec{AC}\)
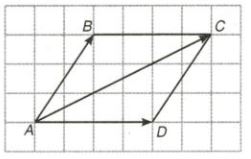
b) Quy tắc hình bình hành: Cho ABCD là hình bình hành, ta luôn có:
\(\vec{AB}+\vec{AD}=\vec{AC}\)
1.4. Quy tắc trung điểm và trọng tâm
-
Nếu M là trung điểm của đoạn thẳng AB thì \(\vec{MA}+\vec{MB}=\vec{0}\)
-
Nếu G là trọng tâm của tam giác ABC thì \(\vec{GA}+\vec{GB}+\vec{GC}=\vec{0}\)
1.5. Vectơ đối của một vectơ
Nếu tổng của hai vectơ \(\vec a\) và \(\vec b\) là vectơ không, thì ta nói vectơ \(\vec a\) là vectơ đối của vectơ \(\vec b\), hoặc ngược lại vectơ \(\vec b\) là vectơ đối của vectơ \(\vec a\)
Định nghĩa:
-
Vectơ đối của vectơ \(\vec a\) là vectơ ngược hướng với vectơ \(\vec a\) và có cùng độ lớn với vectơ \(\vec a\).
-
Vectơ đối của vectơ-không cũng là chính nó.
1.6. Hiệu của hai vectơ
Quy tắc hiệu vectơ: Nếu \(\vec{AB}\) là một vectơ đã cho và 1 điểm O bất kì, ta luôn luôn có:
\(\vec{AB}=\vec{OB}-\vec{OA}\)
2. Bài tập minh họa
Câu 1: Vẽ hình bình hành ABCD. Hãy nhận xét về độ dài và hướng của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \)
Hướng dẫn giải
Về độ dài: hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng độ dài
Về hướng: hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có hướng ngược nhau.
Câu 2: Cho \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow 0 \). Hãy chứng tỏ \(\overrightarrow {BC} \) là vectơ đối của \(\overrightarrow {AB} \)
Hướng dẫn giải
Ta có:
\(\begin{array}{l}
\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow 0 \\
\Rightarrow \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CB} = \overrightarrow 0 + \overrightarrow {CB} \\
\Leftrightarrow \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CB} } \right) = \overrightarrow {CB} \\
\Leftrightarrow \overrightarrow {AB} + \overrightarrow {BB} = \overrightarrow {CB} \\
\Leftrightarrow \overrightarrow {AB} = \overrightarrow {CB} = - \overrightarrow {BC} \\
\Rightarrow \overrightarrow {AB} = - \overrightarrow {BC}
\end{array}\)
Vậy \(\overrightarrow {BC}\) là véc tơ đối của \(\overrightarrow {AB} \).
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho hình bình hành ABCD. Chứng minh rằng: \(\overrightarrow {AB} - \overrightarrow {AC} + \overrightarrow {AD} = \vec 0\)
Câu 2: Cho tứ giác ABCD. AC và BD cắt nhau tại O. Chứng minh rằng nếu \(\overrightarrow {AB} - \overrightarrow {AC} + \overrightarrow {AD} = \vec 0\) thì
a) \(\overrightarrow {AO} = \overrightarrow {OC} .\)
b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC vuông tại A có \(AB = \sqrt 5 ,AC = 2\sqrt 5 \). Độ dài vectơ \({\overrightarrow {AB} + \overrightarrow {AC} }\) bằng:
A. \(\sqrt 5 \)
B. \(5\sqrt 5 \)
C. 25
D. 5
Câu 2: Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Cặp vectơ nào trong số các cặp vectơ sau đây không bằng nhau?
A. \(\overrightarrow {NC} + \overrightarrow {MC} \) và \(\overrightarrow {AD} \)
B. \(\overrightarrow {AM} + \overrightarrow {CD} \) và \(\overrightarrow {ND} \)
C. \(\overrightarrow {AB} - \overrightarrow {NC} \) và \(\overrightarrow {MB} \)
D. \(\overrightarrow {AM} + \overrightarrow {AN} \) và \(\overrightarrow {AB} + \overrightarrow {AD} \)
Câu 3: Cho tam giác ABC. Vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) có giá trị chứa đường thẳng nào sau đây?
A. Tia phân giác của góc A
B. Đường cao hạ từ đỉnh A của tam giác ABC
C. Đường trung tuyến qua A của tam giac ABC
D. Đường thẳng BC
Câu 4: Cho 2 điểm phân biệt A và B. Tập hợp các điểm O thỏa mãn \(\vec{OA}=\vec{OB}\) là:
A. Trung điểm của AB
B. Là 1 khoảng cách sao cho OA=2OB
C. Mọi vị trí
D. Không tồn tại O
Câu 5: Vectơ đối của tổng sau \(\vec{a}+\vec{b}-\vec{c}\) là:
A. \(\vec{a}-\vec{b}+\vec{c}\)
B. \(\vec{b}-\vec{c}+\vec{a}\)
C. \(\vec{c}-\vec{b}-\vec{a}\)
D. \(\vec{a}-\vec{c}+\vec{b}\)
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Tổng và hiệu của hai vectơ Toán 10 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Cách xác định tổng, hiệu hai véctơ, quy tắc ba điểm, quy tắc hình bình hành.
- Các tính chất của tổng véctơ, tính chất của véctơ - không.