Toán 8 Chương 1 Bài 2: Hình thang

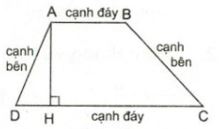
- Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song. Các cạnh song song gọi là cạnh đáy.

- Tính chất: Trong một hình thang, hai góc kề một cạnh bên thì bù nhau

- Chú ý: Để chứng minh một tứ giác là hình thang, ta chứng minh nó có 2 cạnh đối song song.

- Định  nghĩa: Hình thang có một góc vuông là hình thang vuông.

- Chú ý: Để chứng minh một hình thang là vuông, ta chứng minh nó có 1 góc vuông.

- Định nghĩa: Hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau.

- Định lí 1: Trong một hình thang cân, hai cạnh bên bằng nhau.

Ví dụ: ABCD là hình thang có \({\rm{\hat A = \hat B }} \Rightarrow {\rm{ AD = BC}}\)

- Định lí 2: 

• Trong một hình thang cân thì hai đường chéo bằng nhau.
• Ngược lại, một hình thang có hai đường chéo bằng nhau thì nó là hình thang cân.

Ví dụ: ABCD là hình thang cân  \( \Leftrightarrow {\rm{ AC = AD}}\).

Chú ý: Để chứng minh là một hình thang lầ cân, ta có hai cách chứng minh:

• Chứng minh nó là hình thang có hai góc kề một đáy bằng nhau (định nghĩa).
• Chứng minh nó là hình thang có hai đường chéo bằng nhau (định lí 2).

a) Đường trung bình của tam giác

- Định lí 1: Đường thẳng đi qua trung điểm của một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.

- Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

- Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng một nửa cạnh ấy.

Ví dụ: \(\Delta {\rm{ABC}}\); DE là đường trung bình \( \Rightarrow {\rm{ DE}}\parallel {\rm{ BC }}\) và \({\rm{ DE = }}\frac{1}{2}{\rm{BC}}\).

b) Đường trung bình của hình thang

- Định lí 1: Đường thẳng đi qua trung điểm của một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của cạnh bên còn lại.

- Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối các trung điểm của 2 cạnh bên.

- Định lí 2: Đường trung bình của hình thang thì song song với hai đáy và bằng một nửa tổng hai đáy.

Ví dụ: EF là đường trung bình của hình thang ABCD  \( \Rightarrow {\rm{ EF}}\parallel {\rm{AB}}\parallel {\rm{CD}}\) và \({\rm{ EF = }}\frac{1}{2}({\rm{AB + CD)}}\)

Câu 1. Cho ba điểm A, B, C, D theo thứ tự ấy nằm trên một đường thẳng d, biết AB > BC. Trong một nửa mặt phẳng bờ là đường thẳng d vẽ hai tam giác đều ADB, BEC. Gọi M, N, P, Q, I theo thứ tự là trung điểm của các đoạn BD, AE, BE, CD và DE.

a. Chứng minh ba điểm I, M, N  thẳng hàng, ba điểm I, Q, P cũng thẳng hàng.

b. Chứng minh tứ giác MNPQ là hình thang cân.

c. Suy ra: \(NQ = \frac{1}{2}DE\)

Hướng dẫn giải

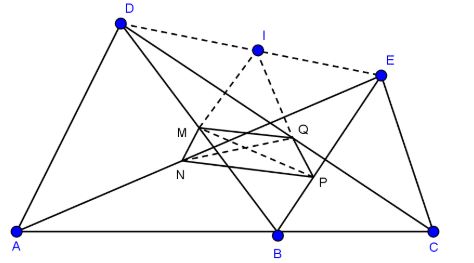
a. Dễ thấy AD // BE.  Trong tam giác AED, I là trung điểm của DE và N là trung điểm của AE nên IN là đường trung bình ứng với cạnh AD, như vậy: IN // AD.

Trong tam giác BDE, I là trung điểm của DE và M là trung điểm của DB nên IM là đường trung bình ứng với cạnh BE, như vậy: IM // BE.

Từ các kết luận IN // AD, IM // BE mà AD // BE, theo tiên đề Euclide, ta suy ra IN và IM trùng nhau hy ba điểm I, M, N thẳng hàng.

Chứng minh tương tự, ta có ba điểm I, Q, P cũng thẳng hàng.

b. Trong tam giác AEB, N là trung điểm của EA và P là trung điểm của EB nên ta có NP // AB

Tương tự ta có: MQ // BC

Vậy MQ // NP hay tứ giác MNPQ là hình thang (1)

Do MN // AD và NP // AB mà \(\widehat {DAB} = {60^0} \Rightarrow \widehat {MNP} = {60^0}\)

Lí luận tương tự, ta có: \(\widehat {QPN} = {60^0}\) cho ta \(\widehat {MNP} = \widehat {QPN}\) (2)

Từ (1) và (2) suy ra tứ giác MNPQ là hình thang cân.

c. Tứ giác MNPQ là hình thang cân, nên hai đường chéo của nó phải bằng nhau: NQ = MP

Trong tam giác DBE, M là trung điểm của BD và P là trung điểm của BE, cho ta: \(MP = \frac{1}{2}DE\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4)\)

Từ (3) và (4) suy ra: \(NQ = \frac{1}{2}DE\)

Chú ý:

- Ta có thể chứng minh ba điểm I, M, N thẳng hàng như sau:

• Trong tam giác AED và N là trung điểm của EA nên IN là đường trung bình ứng với cạnh AD, cho ta: IN // AD mà AD // BE nên IN // BE.
• Trong tam giác BDE, ta có IN // BE mà I là trung điểm cạnh ED, nên đường thẳng IN chứa đường trung bình ứng với cạnh BE. Vậy IN phải đi qua trung điểm của cạnh DB hay ba điểm I, M, N thẳng hàng.

- Có thể thay câu hỏi ba điểm I, M, N thẳng hàng và ba điểm I, Q, P thẳng hàng bằng câu hỏi chứng minh ba đường thẳng MN, QP và DE đồng quy.

Câu 2: Cho tam giác ABC. Trên AC lấy một điểm B’ sao cho AB’=AB và trên AB lấy một điểm C’ sao cho AC’=AC. Chứng minh tứ giác BB’CC’ là hình thang.

Hướng dẫn giải

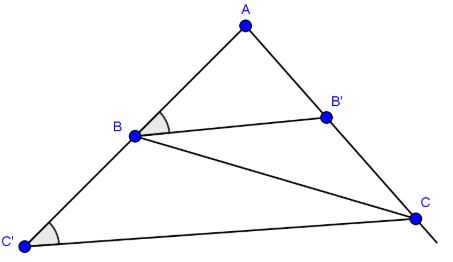
\(AB' = AB \Rightarrow \Delta BAB'\)cân tại đỉnh A, ta có

\(\angle AB{B^\prime } = \frac{{{{180}^0} - \angle A}}{2}\,\,\,\,\,\,\,(1)\)

\(AC' = AC \Rightarrow \Delta CAC'\) cân tại đỉnh A, ta có

\(\angle AC'C = \frac{{{{180}^0} - \angle A}}{2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,(2)\)

Từ (1) và (2) suy ra \(\widehat {ABB'} = \widehat {AC'C}\)

Hai đường thẳng BB’ và CC’ tạo với đường thẳng AB hai góc đồng vị bằng nhau nên BB’ // CC’

Vậy BB’ //CC’ là hình thang.

Câu 3: Cho hình thang ABCD (AB // CD). Gọi E  là giao điểm của hai đường thẳng AD và BC. Gọi M, N, P, Q theo thứ tự là các trung điểm của các đoạn thẳng AE, BE, AC và BD. Chứng minh tứ giác MNPQ là hình thang.

Hướng dẫn giải

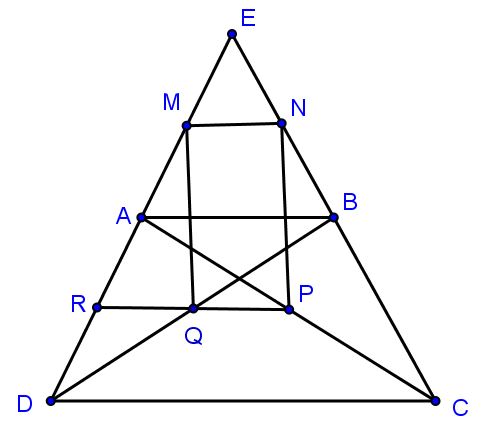
M là trung điểm của AE.

N là trung điểm của BE.

\( \Rightarrow \) MN là đường trung bình ứng với cạnh AB của \(\Delta EAB\), suy ra MN // AB  (1)

Gọi R là trung điểm của AD

Trong \(\Delta ADB,\,\,RQ\) là đường trung bình, suy ra RQ // AB

Trong \(\Delta CAD,\,\,RP\)là đường trung bình, suy ra RP // DC mà DC // AB nên RP // AB.

RQ và RP cùng đi qua R và cùng song song với AB nên theo tiên đề Ơclit thì \(RQ \equiv RP\)

Từ đây ta suy ra QP // AB (2)

Từ (1) và (2) suy ra MN // PQ \( \Rightarrow \) Tứ giác MNPQ là hình thang.

Câu 1: Cho hình thang ABCD đáy lớn  AB; M, N, P, Q theo thứ tự là các trung diểm của các đoạn thẳng AD, BC, AC, BD.

a. Chứng minh bốn điểm M, N, P, Q nằm trên một đường thẳng.

b. Cho AB = a, CD = b với a > b. Tính độ dài các đoạn thẳng MN, PQ.

c. Chứng minh rằng nếu MP = PQ= QN thì a – 2b = 0.

Câu 2: Cho tứ giác ABCD. Các đường phân giác của các góc trong tại đỉnh A và đỉnh D vuông góc với nhau và cắt nhau tại điểm N. Gọi M, P, N, Q theo thứ tự là:

- Giao điểm các tia phân giác của các góc ngoài tại đỉnh A và đỉnh D.

- Giao điểm các tia phân giác trong của các góc tại đỉnh B và đỉnh C.

- Giao điểm của các tia phân giác các góc ngoài tại đỉnh B và đỉnh C.

a. Chứng minh tứ giác ABCD là hình thang.

b. Chứng minh bốn điểm M, N, P, Q thẳng hàng.

c. Tính độ dài của các đoạn thẳng MQ, NP theo các cạnh AB, DC, AD, BC của hình thang.

Câu 3: Cho hình thang ABCD, đáy AB = 40cm, CD = 80cm, cạnh BC = 50cm và AD = 30cm. Chứng minh ABCD là hình thang vuông.

Câu 1: Phát biểu nào sau đây là đúng về định nghĩa của hình thang?

A. Hình thang là tứ giác có các cạnh đối song song

B.  Hình thang là tứ giác có hai cạnh đối bằng nhau

C.  Hình thang là tứ giác có hai cạnh đối song song

D. Hình thang là tứ giác có các cạnh đối bằng nhau

Câu 2:  Một hình thang có một cặp góc đối là  \({120^0}\) và \(\,{80^{0\,}}\), cặp góc đối còn lại của hình thang đó là?

A. \({75^0};\,\,{105^0}\)

B. \(\,{60^0};\,{100^0}\,\)

C. \({115^0}\,;\,{65^0}\)

D. \(\,{75^0};\,\,{115^0}\)

Câu 3: Chọn ý đúng

A. Trong một hình thang, hai góc kề một cạnh bên thì phụ nhau

B. Trong một hình thang, hai góc kề một cạnh bên thì bù nhau

C. Trong một hình thang, hai góc kề một đáy thì bù nhau

D. Trong một hình thang, hai góc kề một đáy thì phụ nhau

Câu 4: Chọn phát biểu đúng

A. Tứ giác có một góc vuông là hình thang vuông

B. Hình thang có một góc vuông là hình thang vuông

C. Tứ giác có hai đường chéo vuông góc là hình thang vuông

D. Hình thang có hai đường chéo vuông góc là hình thang vuông

Câu 5: Cho hình thang ABCD  (AB||CD) có \(\angle A = {80^{0\,}}\,;\angle B = {60^0}\), số đo \(\angle C = ?;\angle D = ?\)

A. \(\angle C = {100^0};\angle D = {120^0}\)

B. \(\angle C = {110^0};\angle D = {120^0}\)

C. \(\angle C = {120^0};\angle D = {110^0}\)

D. \(\angle C = {120^0};\angle D = {100^0}\)

Qua bài học này, các em cần đạt được những yêu cầu sau:

• Nắm được khái niệm hình thang.
• Nhận biết được hình thang.
• Ghi nhớ được tính chất của hình thang.
• Vận dụng kiến thức giải được một số bài toán liên quan.