Toán 8 Chương 2 Bài 2: Diện tích hình chữ nhật

Số đo của một phần măt phẳng giới hạn bởi một đa giác được gọi là diện tích đa giác đó.

Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương.

Diện tích đa giác có các tính chất  sau:

- Hai tam giác bằng nhau thì có diện tích bằng nhau.

- Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.

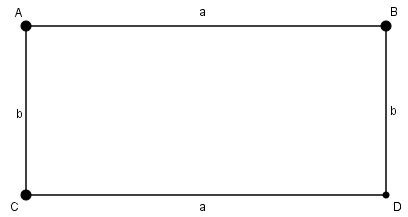
Diện tích hình chữ nhật bằng tích hai kích thước của nó \(  S = a.b\)

(\(S\) là diện tích, \(a\) là chiều dài, \(b\) là chiều rộng của hình chữ nhật).

Diện tích hình vuông bằng bình phương cạnh của nó: \(S = {a^2}\)

Diện tích tam giác vuông bằng nửa tích của hai cạnh góc vuông: \(S = \dfrac{1}{2}ab\)

 Diện tích hình chữ nhật thay đổi như thế nào nếu :

a) Chiều dài tăng hai lần, chiều rộng không đổi

b) Chiều dài và chiều rộng tăng 3 lần.

c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần.

Hướng dẫn giải

Gọi chiều dài và chiều rộng của một hình chữ nhật lần lượt là a,b

Diện tích hình chữ nhật là Shcn = a.b.

a) Nếu chiều dài tăng lên 2 lần, chiều rộng không đổi thì khi đó chiều dài, chiều rộng mới là là 2a và b

Diện tích hình chữ nhật mới là Sm = 2a.b = 2S.

⇒ Diện tích hình chữ nhật tăng lên 2 lần.

b) Nếu chiều dài và chiều rộng tăng lên 3 lần thì chiều dài, chiều rộng mới là 3a,3b

Diện tích hình chữ nhật mới là Sm = 3a.3b = 9S.

⇒ Diện tích hình chữ nhật tăng lên 9 lần.

c) Nếu chiều dài tăng 4 lần, chiều rộng giảm đi 4 lần thì chiều dài, chiều rộng mới là 4a, 1/4b

Diện tích hình chữ nhật mới là Sm = 4a. 1/4b = ab = S.

⇒ Diện tích hình chữ nhật không đổi.

Tính độ dài các cạnh hình chữ nhật biết rằng: Bình phương độ dài một cạnh là 16cm và diện tích hình chữ nhật là 28cm²

Hướng dẫn giải

Gọi hai kích thước của hình chữ nhật là a,b ( a > 0, b > 0 ). Khi đó diện tích của hình chữ nhật là Shcn = a.b

Theo bài ra ta có: x.y = 28    ( 1 ) và x2 = 16 = 42 ⇔ x = 4 (vì x > 0 ), trường hợp y2 = 16 tương tự.

Thay x = 4 vào đẳng thức ( 1 ) ta có: 4y = 28 ⇔ y = 7.

Với x = 4,y = 7 thỏa mãn yêu cầu điều kiện.

Vậy hai kích thức của hình chữ nhật là 4cm, 7cm

Một gian phòng có nền hình chữ nhật với kích thước là \(4,2\,m\) và \(5,4\,m\) có một cửa sổ hình chữ nhật kích thước là \(1\,m\) và \(1,6\,m\) và một cửa ra vào hình chữ nhật kích thước là \(1,2\,m\) và \(2\,m.\)

Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng \(20\%\) diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sáng hay không?

Hướng dẫn giải

Diện tích nền nhà là: \(S = 4,2.5,4 = 22,68\) (\({m^2}\))

Diện tích cửa sổ là: \({S_1}= 1. 1,6 = 1,6\) (\({m^2}\))

Diện tích cửa ra vào là: \({S_2}=1,2.2 = 2,4\) (\({m^2}\))

Diện tích các cửa là: \(S' = {S_1} + {S_2}= 1,6 + 2,4 = 4\) (\({m^2}\))

Ta có \(\dfrac{S^{'}}{S} = \dfrac{4}{22,68}.100\%≈ 17,64\% < 20\%.\) 

Vậy gian phòng không đạt mức chuẩn về ánh sáng.

Câu 1: Hình chữ nhật có chiều dài giảm đi 5 lần và chiều rộng tăng lên 5 lần, khi đó diện tích của hình chữ nhật 

A. Không thay đổi 

B. Tăng 5 lần 

C. Giảm 5 lần

D. Tăng 3 lần

Câu 2: Một hình chữ nhật có diện tích 24 cm2, chiều dài là 8cm. Chi vi hình chữ nhật đó là:

A. 11 cm

B. 20 cm

C. 22 cm

D. 16 cm

Câu 3: Chọn câu đúng

A. Diện tích tam giác vông bằng nửa tích hai cạnh góc vuông 

B. Diện tích hình chữ nhật bằng nửa tích hai kích thuóc của nó 

C. Diện tích hình vuông có cạnh a là 2a

D. Tất cả các đáp án trên đều đúng 

Câu 4: Cho tam giác ABC, biết diện tích tam giác 16cm2 và cạnh BC = 8cm. Đường cao ứng với cạnh BC là:

A. 5 cm

B. 8 cm

C. 6 cm

D. 4 cm

Câu 5: Cho tam giác ABC, lấy M thuộc BC sao cho BM = 3CM. Hãy chọn câu sai:

A. \({S_{ABM}} = \frac{3}{4}{S_{ABC}}\)

B. SABM = 3SAMC

C. \({S_{AMC}} = \frac{1}{3}{S_{ABC}}\)

D. SABC = 4SAMC

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm vững công thức tính diệt tích hình chữ nhật,hình vuông, tam giác vuông.
• Hiểu rằng để chứng minh các công thức tính diện tích trên cần vận dụng các tính chất của diện tích đa giác.