Toán 8 Chương 1 Bài 12: Hình vuông

Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

Từ định nghĩa này ta suy ra:

- Hình vuông là hình chữ nhật có hai cạnh kề bằng nhau.

- Hình vuông là hình thoi có một góc vuông.

Vì hình vuông vừa là hình chữ nhật, vừa là hình thoi nên hình vuông có tất cả tính chất của hình chữ nhật (Chẳng hạn: hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường) và  có tất cả các tính chất của hình thoi (chẳng hạn: hai đường chéo vuông góc với nhau và mỗi đường chéo là phân giác của các góc ở đỉnh), đặc biệt ta có thể phát biểu định lí:

Trong hình vuông, hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

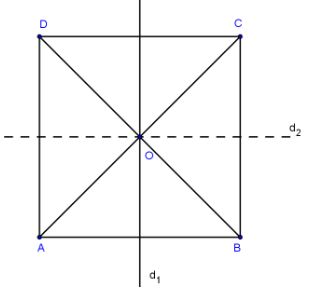
- Hình vuông có một tâm đối xứng là giao điểm của hai đường chéo.

- Hình vuông có bốn trục đối xứng là hai đường chéo và hai đường thẳng nối các trung điểm của các cạnh đối diện.

Để chứng minh một hình vuông, ta chứng minh:

- Hình chữ nhật có hai cạnh kề bằng nhau.

- Hình chữ nhật có hai đường chéo vuông góc với nhau.

- Hình chữ nhật có một đường chéo là đường phân giác của một góc

- Hình thoi có một góc vuông.

- Hình thoi có hai đường chéo bằng nhau.

Câu 1: Trên một đường thẳng xy, lấy ba điểm A, B, C theo thứ tự ấu và AB > BC. Trong cùng một nửa mặt phẳng bờ là đường thẳng xy, vẽ các hình vuông ABDE và BCFG. Một điểm H thuộc đoạn thẳng AB và một điểm K thuộc tia đối của tia DB sao cho AH = DK = BG. Chứng minh rằng EHFK là hình vuông.

Hướng dẫn giải:

Ta có: \(\Delta EAK = \Delta KGF = \Delta HCF = \Delta EAH\)

\( \Rightarrow EK = KF = FH = HE\)

\( \Rightarrow \) EHFK là hình thoi (1)

\(\Delta EDK = \Delta KGF \Rightarrow \widehat {{E_1}} = \widehat {{K_1}}\)

Mà \(\widehat {{E_1}} = \widehat {{K_2}} = {90^0} \Rightarrow \widehat {{K_1}} + \widehat {{K_2}} = {90^0}\)

\( \Rightarrow \widehat {EKF} = {90^0}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\)

Từ (1) và (2) suy ra đpcm.

Câu 2: Cho tam giác ABC vuông góc tại đỉnh A, kẻ đường cao AH và  trung tuyến AM. Đường phân giác của góc A cắt đường trung trực của cạnh BC tại điểm D. Từ D kẻ DE vuông góc với BC và DF vuông góc với AC. Chứng minh:

a. AD là phân giác của góc HAM.

b. Ba điểm E, M, F thẳng hàng.

c. Tam giác BDC là tam giác vuông cân.

Hướng dẫn giải:

a. Ta có:

\(\widehat {{C_1}} = \widehat {{A_1}}\) (cùng phụ với \(\widehat B\))

\(\widehat {{C_1}} = \widehat {{A_2}}\) (\(\Delta AMC\)cân)

Suy ra \(\widehat {{A_3}} + \widehat {{A_4}}\)

\( \Rightarrow \) AD là phân giác của góc HAM.

b. AH // DM \( \Rightarrow \widehat {{D_1}} = \widehat {{A_4}}\) mà \(\widehat {{A_4}} = \widehat {{A_3}}\)

\( \Rightarrow \widehat {{D_1}} = \widehat {{A_3}} \Rightarrow \Delta AMD\) cân

\( \Rightarrow \) MA = MD.

Ta dễ dàng chứng minh được AEDF là hình vuông, cho ta

EA = ED; FA = FD

Như vậy cả ba điểm E, M, F đều nằm trên đường trung trực của đoạn thẳng AD.

c. \(\Delta BED = \Delta CFD \Rightarrow \widehat {{D_2}} = \widehat {{D_3}}\)

\(\widehat {BDC} = \widehat {BDF} + \widehat {{D_3}} = \widehat {BDF} + \widehat {{D_2}} = \widehat {EDF} = {90^0}\)

Kết hợp với DB = DC suy ra đpcm.

Câu 3: Cho hình vuông ABCD. Từ một điểm M thuộc đường chéo BD, ta kẻ ME vuông góc với AB và MF vuông góc với AD. Chứng minh:

a. DE = CF và \(DE \bot CF.\)

b. CM = EF và \(CM \bot {\rm{EF}}{\rm{.}}\)

c. BF = CE và \(BF \bot CE.\)

d. Qua các kết quả trên, có thể kết luận gì vị trí tương đối của các đường thẳng DE, CM và BF?

Hướng dẫn giải:

a. \(\Delta EAD = \Delta FDC\)

\( \Rightarrow DE = CF\) và \(\widehat {{C_1}} = \widehat {{D_1}}\)

Ta có \(\widehat {{C_1}} + \widehat {{F_1}} = {90^0}\)

\(\begin{array}{l} \Rightarrow \widehat {{D_1}} + \widehat {{F_1}} = {90^0}\\ \Rightarrow \widehat {DKF} = {90^0}\\ \Rightarrow DE \bot CF.\end{array}\)

b. ABCD là hình vuông; \(M \in BD\)

\( \Rightarrow \) MA = MC.

AEMF là hình chữ nhật \( \Rightarrow \) MA = EF. Vậy CM = EF.

\(\Delta CNM = \Delta EAF \Rightarrow \widehat {{C_2}} = \widehat {AEF}\)

\(AB//FN \Rightarrow \widehat {EKM} = \widehat {{M_1}}\) (đồng vị)

\(\widehat {EKM} + \widehat {AEF} = \widehat {{C_2}} + \widehat {{M_1}} = {90^0} \Rightarrow \widehat {KIE} = {90^0} \Rightarrow CM \bot {\rm{EF}}\)

c.

 \(\begin{array}{l}\Delta B{\rm{AF = }}\Delta {\rm{CBE}} \Rightarrow BF = CE \Rightarrow \widehat {ABF} = \widehat {BCE}\\ \Rightarrow \widehat {BEC} + \widehat {ABF} = \widehat {BEC} + \widehat {BCE} = {90^0} \Rightarrow \widehat {EHB} = {90^0}\\ \Rightarrow BF \bot CE.\end{array}\)

d. Trong tam giác CEF thì DE, CM và DF là các đường cao nên chúng đồng quy.

Chú ý: Trong bài này, để chứng minh hai đường thẳng vuông góc, ta chứng minh rằng chúng tạo với mội đường thẳng thứ ba một tam giác có tổng hai góc bằng \({90^0}\)

Để chứng minh ba đường thẳng đồng quy, ta chứng minh chúng là những đường thẳng đặc biệt trong tam giác (đường cao, đường trung tuyến, đường phân giác, đường trung trực).

Câu 1: Cho tam giác ABC vuông tại đỉnh A và AB < AC. Kẻ đường cao AH. Trong nửa mặt phẳng có chứa đỉnh A, bờ là đường thẳng BC, vẽ hình AHDE.

a. Chứng minh điểm D thuộc đoạn thẳng HC.

b. Gọi F là giao điểm của DE và AC. Đường thẳng qua F song song với AB cắt đường thẳng qua B song song với AC tại điểm G. Chứng minh tứ giác ABGF là hình vuông.

c. Chứng minh ba đường thẳng AG, BF và HE đồng quy.

d. Chứng minh tứ giác DEHG là hình thang.

Câu 2: Cho đoạn thẳng AB = a và một điểm M bất kì thuộc đoạn thẳng ấy. Trong cùng một nửa mặt phẳng bờ là đường thẳng AB, vẽ các hình vuông AMCD, BMEF.

a. Chứng minh  tại một điểm mà ta gọi là H.

b. Chứng minh D, H, F thẳng hàng.

c. Gọi I là trung điểm của đoạn  thẳng DF. Tính khoảng cách từ điểm I đến đường thẳng AB theo a; suy ra rằng I là điểm cố định, không phụ thuộc vào vị trí của điểm M trên đoạn thẳng AB.

d. Chỉ rõ rằng đường thẳng BE đi qua I. Khi điểm M di chuyển trên đoạn thẳng AB thì đỉnh C của hình vuông BMEF di chuyển trên những đường thẳng cố định nào?

Câu 3: Một góc vuông xAy quay quanh đỉnh A của hình vuông ABCD. Cạnh Ax cắt các đường thẳng BC và CD theo thứ tự tại các điểm M, N và cạnh Ay cắt các đường thẳng BC, CD theo thứ tự tại các điểm P, Q.

a. Chứng minh các tam giác NAP, MAQ là các tam giác vuông cân.

b. Gọi E là giao điểm của QM và PN; F và I theo thứ tự là trung điểm của các đoạn thẳng QM và PN. Chứng minh tứ giác AFEU là hình chữ nhật.

c. Khi góc vuông xAy quay quanh đỉnh A thì các điểm F, I di chuyển trên đường thẳng cố định nào?

Câu 1:  Các dấu hiệu nhận biết sau, dấu hiệu nào không đủ để kết luận tứ giác là hình vuông

A.  Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông

B.  Hình chữ nhật có hai đường chéo vuông góc nhau là hình vuông

C.  Hình bình hành có hai đường chéo bằng nhau là hình vuông

D.  Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông

Câu 2:  Cho hình vuông có cạnh bằng 2a, độ dài đường chéo của hình vuông là 

A. \(a\sqrt 2 \,\)

B. \(2a\sqrt 2 \)

C. \(\frac{{a\sqrt 2 }}{2}\)

D. \(\frac{{3a}}{{\sqrt 2 }}\)

Câu 3:  Cho đường chéo hình vuông là \(4\sqrt 2 \) cm thì diện tích hình vuông có giá trị là bao nhiêu?

A. 32cm²

B. 16cm²

C. 8cm²

D. 2cm²

Câu 4: Một hình vuông có chu vi là 28 cm, hỏi diện tích hinh vuông nhận giá trị nào sau đây?

A. 49cm²

B.  49cm²

C. 14cm²

D. 14cm²

Câu 5:  Chọn ý sai

A.  Hình thoi có một góc vuông là hình vuông.

B.  Tứ giác vừa là hình thoi vừa là hình chữ nhật thì nó là hình vuông.

C. Tứ giác có bốn cạnh bằng nhau là hình vuông.

D.  Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Qua bài giảng Hình vuông này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như : 

• Nhận biết được hình vuông.

• Ghi nhớ được tính chất, dấu hiệu nhận biết hình vuông.

• Vận dụng kiến thức giải được một số bài toán liên quan.