Toán 6 Chương 1 Bài 1: Tập hợp và phần tử của tập hợp

- Tập hợp một hay nhiều đối tượng có tính chất đặc trưng giống nhau. Những đối tượng gọi là phần tử.

VD:

- Tập hợp các em học sinh lớp 61

- Tập hợp các số tự nhiên là bội số của 10 và nhỏ hơn 100

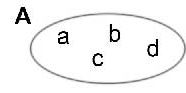
- Tập hợp các chữ cái a, b, c, d

1.2. Cách viết các ký hiệu:

- Tên tập hợp được đặt bằng chữ cái in hoa.

VD: 
A= { 0; 1; 2; 3 }

B= { a; b; c; d }
C= { x \(\in\) N/ x<10}

- Các phần tử được viết trong 2 dấu {}

- Giữa các phần tử được ngăn cách bới dấu “,” hoặc dấu “;”

- Thứ tự các phần tử liệt kê tùy ý

- Mỗi phần tử được liệt kê một lần

- Có hai cách để viết 1 tập hợp là: Liệt kê các phần tử của tập hợp hay chỉ ra tính chất đặc trưng của các phần tử

VD: Viết tập hợp A các số tự nhiên chia 2 dư 1 và nhỏ hơn < 10

A={1,3,5,6,7}

A= {x  \(\in\) N/ x=2k+1; x<10}

Ký hiệu: 

a \(\in\) A đọc a là phần tử của tập hợp A hay phần tử a thuộc tập hợp A.

a \(\notin\) A đọc a không là phần tử của tập hợp A hay phần tử a không thuộc tập hợp A.

- Một tập hợp có thể có một phần tử, có nhiều phần tử, có vô số phần tử, cũng có thể không có phần tử nào là tập hợp rỗng kí hiệu \(\emptyset\).

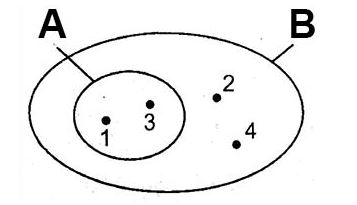
- Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập hợp con của tập hợp B. Kí hiệu: A \(\subset\) B đọc là: A là tập hợp con của tập hợp B hoặc A được chứa trong B hoặc B chứa A.

- Mỗi tập hợp đều là tập hợp con của chính nó và tập hợp rỗng là tập hợp con của mọi tập hợp.

* Cách tìm số tập hợp con của một tập hợp: Nếu A có n phần tử thì số tập hợp con của tập hợp A là 2n.

a. Hãy liệt kê các phần tử của tập hợp A.

b.  Điền kí hiệu thích hợp vào ô vuông

t   [ ]     A;    c   [ ]   A;      h   [ ]    A

Hướng dẫn giải:

a/  A = {a, c, h, i, m, n, ô, p, t}

b/ b \(\notin\) A ; c \(\in\) A; h\(\in\) A

Lưu ý HS: Bài toán trên không phân biệt chữ in hoa và chữ in thường trong cụm từ đã cho.

Câu 2: Cho tập hợp các chữ cái X = {A, C, O}

a/ Tìm cụm chữ tạo thành từ các chữ của tập hợp X.

b/ Viết tập hợp X bằng cách chỉ ra các tính chất đặc trưng cho các phần tử của X.

Hướng dẫn giải:

a/ Chẳng hạn cụm từ “CA CAO” 

b/ X = {x: x-chữ cái trong cụm chữ “CA CAO”}

Câu 3: Cho tập hợp A = {1; 2;3;x; a; b}

a/ Hãy chỉ rõ các tập hợp con của A có 1 phần tử.

b/ Hãy chỉ rõ các tập hợp con của A có 2 phần tử.

c/ Tập hợp B = {a, b, c} có phải là tập hợp con của A không?

Hướng dẫn giải:

a/ {1} { 2} { a } { b} ….

b/ {1; 2} {1; a} {1; b} {2; a} {2; b} { a; b} ……

c/ Tập hợp B không phải là tập hợp con của tập hợp A bởi vì tập hợp B có phần tử c nhưng phần tử c lại không thuộc tập hợp A

Câu 4: Cho tập hợp B = {a, b, c}. Hỏi tập hợp B có tất cả bao nhiêu tập hợp con?

Hướng dẫn giải:

- Tập hợp con của B không có phần từ nào là 1: \(\emptyset\)

- Các tập hợp con của B có một phần tử là 3: {a}, {b}, {c} 

- Các tập hợp con của B có hai phần tử là 3: {a,b}, {a,c}, {b,c} 

- Tập hợp con của B có 3 phần tử chính là 1:  {a, b, c}

Vậy tập hợp A có tất cả là 1+3+3+1 = 8 tập hợp con = 23

Ghi chú: Một tập hợp A bất kỳ luôn có hai tập hợp con đặc biệt là tập hợp rỗng và chính tập hợp A. Nếu A có n phần tử thì số tập hợp con của tập hợp A là 2n.

a. Hãy liệt kê các phần tử của tập hợp A.

b.  Điền kí hiệu thích hợp vào ô vuông

o   [ ]     A;    a   [ ]   A;     b   [ ]    A

Câu 2: Cho tập hợp A = {10; 20;30;x; y; z}

a/ Hãy chỉ rõ các tập hợp con của A có 1 phần tử.

b/ Hãy chỉ rõ các tập hợp con của A có 2 phần tử.

c/ Tập hợp B = {x, y, z} có phải là tập hợp con của A không?

Câu 3: Cho tập hợp B = {x, y, z, t}. Hỏi tập hợp B có tất cả bao nhiêu tập hợp con?

Câu 1: Số liền trước số 11 là:

A. 10

B. 9

C. 11

D. 12

Câu 2: Tập hợp các số tự nhiên không vượt quá 5 gồm bao nhiêu phần tử?

A. 4 phần tử

B. 5 phần tử

C. 6 phần tử

D. 7 phần tử

Câu 3: Tập hợp các phần tử trong câu " HỌC247" gồm bao nhiêu phần tử

A. 4 phần tử

B. 5 phần tử

C. 6 phần tử

D. 7 phần tử

Câu 4: Số liền sau số 77 là:

A. 80

B. 79

C. 77

D. 78

Câu 5: Số cần điền vào dấu "..." để được một chiều tăng dần hơn kém nhau 3 đơn vị là:

35,...,...

A. 32;29

B. 38;41

C. 34;33

D. 36;37

Câu 6: Tập hợp E các số tự nhiên lớn hơn 7 và nhỏ hơn 12 được biểu diễn như thế nào? Chọn một phương án đúng:

A. E = {8 ; 9 ; 10 ; 11 ; 12}

B. E = {8 ; 9 ; 10 ; 11}

C. E = {7 ; 8 ; 9 ; 10 ; 11}

D. E = {7 ; 8 ; 9 ; 10 ; 11}

Câu 7: Cho hai tập hợp \(B = \left\{ {a;b} \right\};P = \left\{ {b;x;y} \right\}\). Chọn nhận xét sai

A. \(b \in B\)

B. \(x \in B\)

C. \(a \notin P\)

D. \(y \in P\)

Câu 8: Cho tập hợp B = {17; 19; 20; 21; 23}. Chọn đáp án đúng 

A. \(15 \in B\)

B. \(23 \in B\)

C. \(19 \notin B\)

D. \(15 \in B\) và \(23 \in B\)

Câu 9: Tập hợp S các tháng của quý bốn trong năm là 

A. S = {tháng Bảy, tháng Tám, tháng Chín}

B. S = {tháng Tư, tháng Năm, tháng Sáu}

C. S = {tháng Một, tháng Hai, tháng Ba}

D. S= {tháng Mười, tháng Mười Một, tháng Mười Hai}

Câu 10: Tập hợp các chữ cái có trong từ "VUI HOC 247" là 

A. A = {V; U; I; H; O; C}

B. A = {V; U; I; H; O; C; 2; 4; 7}

C. A = {V; U; I;2; 4; 7}

D. A = {V; U; I; H; O; 2; 4}