Toán 7 Chương 3 Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Mời các em cùng tham khảo nội dung bài giảng dưới dây do eLib tổng hợp và biên soạn. Bài học sẽ giới thiệu đến các em kiến thức về Quan hệ giữa góc và cạnh đối diện trong một tam giác cùng với những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng nắm đươc nội dung phần này.
Mục lục nội dung

Toán 7 Chương 3 Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
1. Tóm tắt lý thuyết
Định lí 1: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
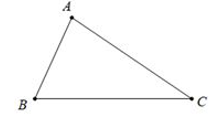
Ví dụ 1: Tam giác ABC nếu AC > AB thì
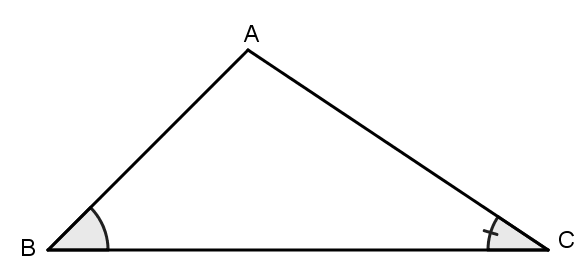
Định lí 2: Trong một tam giác cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Ví dụ 2: Tam giác ABC nên thì AC > AB
Nhận xét:
- Trong
- Trong tam giác tù (hoặc tam giác vuông), góc tù (hoặc góc vuông) là góc lớn nhất nên cạnh đối diện với góc tù (hoặc góc vuông) là cạnh lớn nhất.
2. Bài tập minh họa
Câu 1: Cho vuông tại A (AB < AC).
Tia phân giác của cắt AC tại D, qua C vẽ đường vuông góc với AC cắt tia đối của tia DB tại I. Chứng minh AB < CI; AC < CI.
Hướng dẫn giải
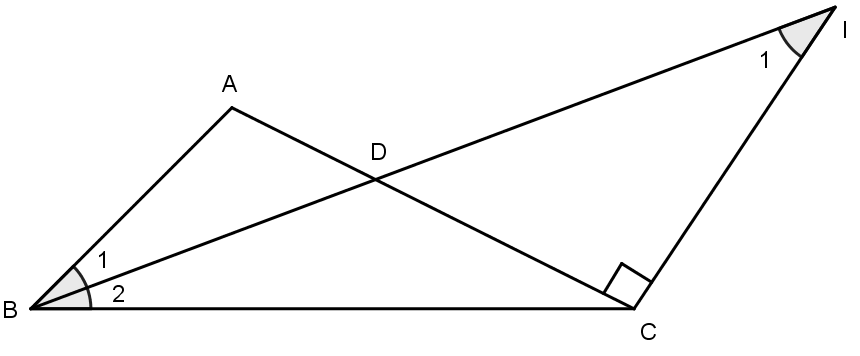
Ta có: (BD là tia phân giác ) mà AB // CI (cùng vuông góc với AC
(so le trong)
Vậy cân tại A có AB < BC.
Vậy AB < CI.
Tương tự ta cũng chứng minh được:
AC < CI (vì )
Câu 2: Cho tam giác ABC. Trên tia đối của tia BA người ta lấy điểm D nào đó khác điểm B và trên tia đối của tia CA người ta lấy điểm E sao cho CE = BD. Chứng minh rằng BC nhỏ hơn DE.
Hướng dẫn giải
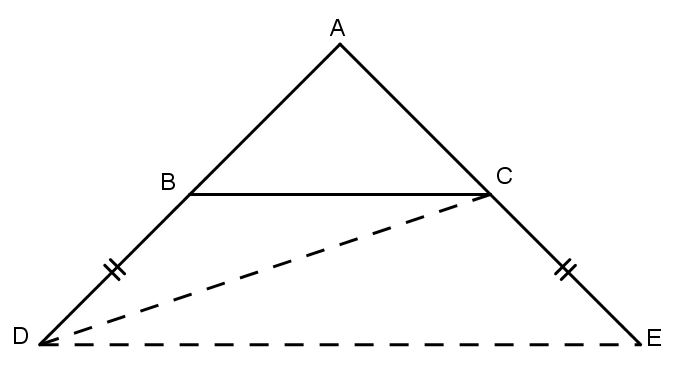
Xét Góc DCE là góc ngoài đỉnh C của tam giác ấy, nên ta có:
Hai tam giác BCD và EDC có hai cạnh bằng nhau từng một đôi.
BD = EC (theo giả thiết)
CD là cạnh chung
Hai góc xen giữa hai cạnh ấy không bằng nhau nên hai cạnh đối diện với hai góc ấy không bằng nhau.
Ta suy ra: BC < DE.
Câu 3: Cho có AC > AB, M là trung điểm của BC. Nối AM. Trên tia đối của MA lấy D sao cho MA = MD. Nối BD. So sánh và .
Hướng dẫn giải
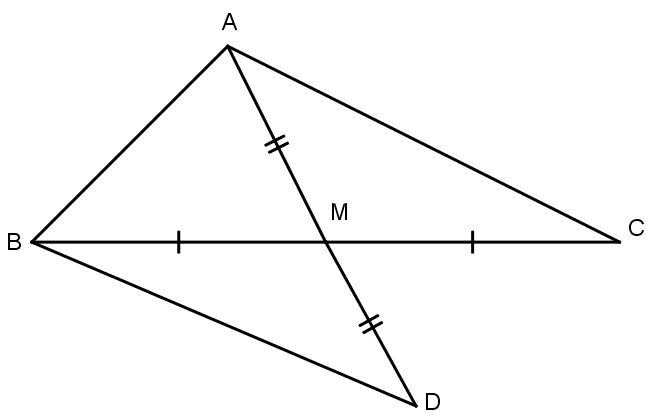
và có:
AM = DM (gt)
MC = BM (gt)
(đối đỉnh)
Nên
Suy ra và AC = DB.
Mà AC > AB (gt)
Trong có
Hay
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho cân tại A. Lấy điểm E trên đoạn BC, lấy điểm F trên đoạn BC kéo dài, điểm D trên AC kéo dài về phía C. Nối AE, AF, BD. Chứng minh:
a. AB < AE
b. AB < AF
c. BD > BC
Câu 2: Cho có 3 cạnh thoả mãn hệ thức AC > CB > BA. Gọi I là giao điểm của các tia phân giác trong của và . Chứng minh IB < IA < IC.
Câu 3: Cho (AC > AB), M là trung điểm của BC. Trên AB và AC lấy 2 điểm P và N sao cho BP = CN. Chứng minh:
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC có (góc B, góc C đều là góc nhọn). Vẽ phân giác AD. So sánh BD và CD
A. Chưa đủ điều kiện để so sánh
B. BD = CD
C. BD < CD
D. BD > CD
Câu 2: Cho tam giác ABC có góc A tù. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F. Chọn câu đúng.
A. BF > EF
B. EF < BC
C. BF < BC
D. Cả A, B, C đều đúng
Câu 3: Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên toa đối của tia MA lấy điểm D sao cho MA = MD. So sánh góc CDA và góc CAD?
A.
B.
C.
D.
Câu 4: Cho tam giác ABC có AB + AC = 10cm, AC - AB = 4cm. So sánh góc B và góc C
A.
B.
C.
D.
Câu 5: Cho tam giác ABC có . Em hãy chọn câu trả lời đúng nhất:
A. AC < AB < BC
B. AB < AC < BC
C. BC < AC < AB
D. AC < BC < AB
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Nắm được mối quan hệ giữa góc và cạnh đối diện trong một tam giác.
- Áp dụng để giải những bài toán liên quan.
Tham khảo thêm
- doc Toán 7 Chương 3 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- doc Toán 7 Chương 3 Bài 3: Quan hệ giữa ba cạnh của một tam giác Bất đẳng thức tam giác
- doc Toán 7 Chương 3 Bài 4: Tính chất ba đường trung tuyến của tam giác
- doc Toán 7 Chương 3 Bài 5: Tính chất tia phân giác của một góc
- doc Toán 7 Chương 3 Bài 6: Tính chất ba đường phân giác của tam giác
- doc Toán 7 Chương 3 Bài 7: Tính chất đường trung trực của một đoạn thẳng
- doc Toán 7 Chương 3 Bài 8: Tính chất ba đường trung trực của tam giác
- doc Toán 7 Chương 3 Bài 9: Tính chất ba đường cao của tam giác