Toán 11 Chương 5 Bài 1: Định nghĩa và ý nghĩa của đạo hàm

Cho hàm số $y = f(x)$ xác định trên khoảng $(a;b)$, $x_0\in (a;b)$. Giới hạn hữu hạn (nếu có) của tỉ số $\frac{f(x)-f(x_{0})}{x-x_{0}}$  khi $x → x_0$ được gọi là đạo hàm của hàm số đã cho tại  $x_0$, kí hiệu là $f'( x_0)$ hay $y'( x_0)$. Như vậy:

$f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}$

Nếu đặt $x - x_0= ∆x$ và $∆y = f(x_0+∆x) - f(x_0)$ thì ta có

$f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \dfrac{{\Delta y}}{{\Delta x}}$

Đại lượng $∆x$ được gọi là số gia của đối số tại $x_0$ và đại lượng $∆y$ được gọi là số gia tương ứng của hàm số.

• Bước 1. Với $∆x$ là số gia của số đối tại $x_0$ ,tính $∆y = f(x_0+∆x)- f(x_0)$;
• Bước 2. Lập tỉ số $\dfrac{\Delta y}{\Delta x}$;
• Bước 3. Tính $\mathop {\lim }\limits_{\Delta x \to 0} \dfrac{{\Delta y}}{{\Delta x}}$.

Nhận xét: nếu thay $x_0$ bởi $x$ ta có định nghĩa và quy tắc tính đạo hàm của hàm số $y = f(x)$ tại điểm $x ∈ (a;b)$.

Định lí: Nếu hàm số $y = f(x)$ có đạo hàm tại $x_0$ thì nó liên tục tại $x_0$.

Chú ý

• Định lí trên tương đương với khẳng định : Nếu $y = f(x)$ gián đoạn tại $x_0$ thì nó không có đạo hàm tại điểm đó.
• Mệnh đề đảo của định lí không đúng. Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.

a) Ý nghĩa hình học của đạo hàm

 Nếu tồn tại, $f'(x_0)$ là hệ số góc của tiếp tuyến của đồ thị hàm số $y = f(x)$ tại điểm $M_0(x_0;f(x_0))$. Khi đó phương trình tiếp tuyến của đồ thị tại điểm $M_0(x_0;f(x_0))$ là

$y - f(x_0) = f'(x_0)(x-x_0)$

b) Ý nghĩa vật lí của đạo hàm

$v(t) = s'(t)$ là vận tốc tức thời của chuyển động $s = s(t)$ tại thời điểm $t$.

a) Cho hàm số y = x². Hãy tính y'(xo) bằng định nghĩa.

b) Cho hàm số y = -x² + 3x – 2. Tính y’(2) bằng định nghĩa.

Hướng dẫn giải

a) 

$\eqalign{ & y'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} {{{x^2} - {x_0}^2} \over {x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} {{(x - {x_0})(x + {x_0})} \over {x - {x_0}}} \cr & = \mathop {\lim }\limits_{x \to {x_0}} (x + {x_0}) = 2{x_0} \cr}$

b) - Giả sử Δx là số gia của đối số tại x_o = 2. Ta có:

Δy = y(2 + Δx) - y(2)

= -(2 + Δx)² + 3(2 + Δx) - 2 - (-2² + 3.2 - 2)

= -(4 + 4Δx + (Δx)² )+ 6 + 3Δx - 2 = - (Δx)² - Δx

$\eqalign{ & \Rightarrow {{\Delta y} \over {\Delta x}} = {{ - {{(\Delta x)}^2} - \Delta x} \over {\Delta x}} = - \Delta x - 1 \cr & \Rightarrow y'(2) = \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} ( - \Delta x - 1) = - 1 \cr}$

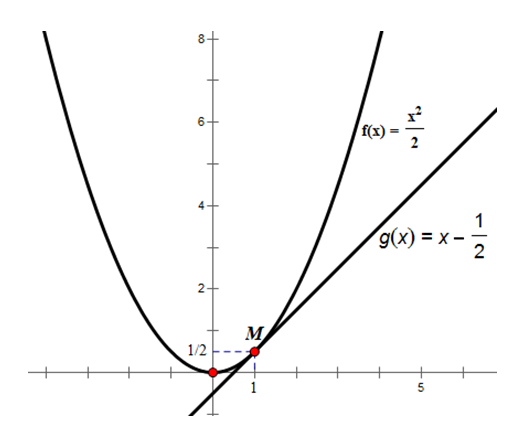
a) Vẽ đồ thị của hàm số f(x) = ${{{x^2}} \over 2}$

b) Tính f’(1).

c) Vẽ đường thẳng đi qua điểm M(1; ${1 \over 2}$) và có hệ số góc bằng f’(1). Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.

Hướng dẫn giải

a) 

b) - Giả sử Δx là số gia của đối số tại xo = 1. Ta có:

$\eqalign{ & \Delta y = f(1 + \Delta x) - f(1) \cr &= {{{{(1 + \Delta x)}^2}} \over 2} - {{{1^2}} \over 2} \cr &= {{{{(\Delta x)}^2} + 2\Delta x} \over 2} \cr  & \Rightarrow {{\Delta y} \over {\Delta x}} = {{{{(\Delta x)}^2} + 2\Delta x} \over 2}:\Delta x \cr &= {{\Delta x} \over 2} + 1 \cr  & \Rightarrow f'(1) = \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} \cr &= \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta x} \over 2} + 1 = 0 + 1 = 1 \cr}$

c) - Đường thẳng có hệ số góc bằng f'(1) = 1 có dạng:

y = 1.x + a hay y = x + a

Mà đường thẳng đó đi qua điểm M(1;1/2) nên có: ${1 \over 2}$ = 1 + a ⇒ a = ${1 \over 2}$ - 1 = -${1 \over 2}$

⇒ đường thẳng đi qua M và có hệ số góc bằng 1 là: y = x – ${1 \over 2}$

Ta có đồ thị như trên. Đường thẳng y = x – ${1 \over 2}$ tiếp xúc với đồ thị hàm số f(x) tại M

Bằng định nghĩa, hãy tính đạo hàm của các hàm số:

a) f(x) = x2 tại điểm x bất kì;

b) g(x) = ${1 \over x}$ tại điểm bất kì x ≠ 0.

Hướng dẫn giải

a) Giả sử Δx là số gia của đối số tại xo bất kỳ. Ta có:

$\eqalign{ & \Delta y = f({x_0} + \Delta x) - f({x_0}) \cr  & = {({x_0} + \Delta x)^2} - {x_0}^2 = 2{x_0}\Delta x + {(\Delta x)^2} \cr  & \Rightarrow {{\Delta y} \over {\Delta x}} = {{2{x_0}\Delta x + {{(\Delta x)}^2}} \over {\Delta x}} = 2{x_0} + \Delta x \cr  & \Rightarrow y'({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} (2{x_0} + \Delta x) = 2{x_0} \cr}$

b) Giả sử Δx là số gia của đối số tại xo bất kỳ. Ta có:

$\eqalign{ & \Delta y = g({x_0} + \Delta x) - g({x_0}) \cr  & = {1 \over {{x_0} + \Delta x}} - {1 \over {{x_0}}} = {{ - \Delta x} \over {{x_0}({x_0} + \Delta x)}} \cr  & \Rightarrow {{\Delta y} \over {\Delta x}} = {{ - \Delta x} \over {{x_0}({x_0} + \Delta x)}}:\Delta x = {{ - 1} \over {{x_0}({x_0} + \Delta x)}} \cr  & y'({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} ({{ - 1} \over {{x_0}({x_0} + \Delta x)}}) = {{ - 1} \over {{x_0}^2}} \cr}$

Câu 1: Tìm số gia của hàm số $f(x) =  x^3$, biết rằng:

a) $x_0 = 1; ∆x = 1$

b) $x_0= 1; ∆x = -0,1$

Câu 2: Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau: 

a) $y = 3x - 5;$

b) $y = 4{x^2} - 0,6x + 7;$

c) $y = 4x - {x^2};$

d) $y = \sqrt {3x + 1} ;$

Câu 3: Cho $f\left( x \right) = \root 3 \of {x - 1} .$  Tính $f'\left( 0 \right);f'\left( 1 \right).$

Câu 4: Cho $\varphi \left( x \right) = {8 \over x}.$ Chứng minh rằng $\varphi '\left( { - 2} \right) = \varphi '\left( 2 \right).$

Câu 1: Trong các phát biểu sau, phát biểu nào sau là đúng?

A. Nếu hàm số $y=f(x)$ không liên tục tại $x_{0}$ thì nó có đạo hàm tại điểm đó.

B. Nếu hàm số $y=f(x)$ có đạo hàm tại $x_{0}$ thì nó không liên tục tại điểm đó.

C. Nếu hàm số $y=f(x)$ có đạo hàm tại $x_{0}$ thì nó liên tục tại điểm đó.

D. Nếu hàm số $y=f(x)$ liên tục tại $x_{0}$ thì nó có đạo hàm tại điểm đó.

Câu 2: Cho f là hàm số liên tục tại $x_{0}$. Đạo hàm của f tại $x_{0}$ là: 

A. $f(x_{0})$

B. $\frac{f(x_{0}+h)-f.(x_{0})}{h}$

C. $\underset{h \to 0}{lim}\frac{f(x_{0}+h)-f(x_{0})}{h}$ ( nếu tồn tại giới hạn).

D. $\underset{h \to 0}{lim}\frac{f(x_{0}+h)-f(x_{0}-h)}{h}$ ( nếu tồn tại giới hạn).

Câu 3: Cho hàm số $y=f(x)$ có đạo hàm tại $x_{0}$ là $f'(x_{0})$. mệnh đề nào sau đây sai?

A. $f'(x_{0})=\underset{x \to x_{0}}{lim}\frac{f(x)-f(x_{0})}{x-x_{0}}$

B. $f'(x_{0})=\underset{\Delta x \to 0}{lim}\frac{f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}$

C. $f'(x_{0})=\underset{h \to 0}{lim}\frac{f(x_{0}+h)-f(x_{0})}{h}$

D. $f'(x_{0})=\underset{x \to x_{0}}{lim}\frac{f(x+x_{0})-f(x_{0})}{x-x_{0}}$

Câu 4: Cho hàm số $f(x)=\begin{cases}\frac{3-\sqrt{4-x}}{4} & \text{ khi } x\neq 0 \\ \frac{1}{4} & \text{ khi } x=0 \end{cases}$. Tính $f'(0)$

A. $f'(0)=\frac{1}{4}$

B. $f'(0)=\frac{1}{16}$

C. $f'(0)=\frac{1}{32}$

D. Không tồn tại.

Câu 5: $\begin{cases}\frac{\sqrt{x^{2}+1}-1}{x} & \text{ khi } x\neq 0 \\ 0 & \text{ khi } x=0 \end{cases}$. Tính $f'(0)$

A. $f'(0)=0$

B. $f'(0)=1$

C. $f'(0)=\frac{1}{2}$

D. Không tồn tại.

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Biết định nghĩa đạo hàm tại một điểm;
• Hiểu rõ rằng đạo hàm của một hàm số tại một điểm là một số xác định;
• Tính được đạo hàm của hàm lũy thừa, hàm đa thức bậc 2 hoặc 3 theo định nghĩa;
• Biết tìm vận tốc tức thời của một chuyển động có phương trình s = f(t)