10 đề thi Học kì 1 môn Toán lớp 12 năm 2020 có đáp án
Đồng hành cùng các bạn học sinh năm nay, eLib giới thiệu chuyên mục bộ 10 đề thi HK1 môn Toán 12. Với lời giải chi tiết, rõ ràng, logic, khoa học, hy vọng bộ tài liệu sẽ giúp các em có thể so sánh, đối chiếu kết quả bài làm của mình, từ đó có kế hoặc thật tốt cho chặng đường tương lai phía trước. eLib sẽ liên tục cập nhật những tài liệu ôn thi và cả đề thi cũng như đáp án môn Toán 12 mới nhất.
Mục lục nội dung

10 đề thi Học kì 1 môn Toán lớp 12 năm 2020 có đáp án
1. Đề thi học kì 1 môn Toán 12 số 1
TRƯỜNG THPT VĨNH PHÚC
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 10
Thời gian: 90 phút (không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM: (3,0 điểm).
Câu 1. Cho hàm số y = f(x) có đạo hàm f′(x)=3x2+1,∀x∈R.Chọn khẳng định đúng trong các khẳng định sau
A.Hàm số y = f(x) đồng biến trên khoảng (0;+∞) và nghịch biến trên khoảng (−∞;0).
B. Hàm số y = f(x) đồng biến trên khoảng (−∞;0) và nghịch biến trên khoảng (0;+∞).
C. Hàm số y = f(x) nghịch biến trên R
D. Hàm số y = f(x) đồng biến trên R
Câu 2. Cho hình hộp chữ nhật ABCD.A'B'C'D'. Mặt phẳng nào sau đây chia hình hộp chữ nhật thành hai phần có thể tích bằng nhau?
A. (ABC'D')
B. (A'C'B)
C. (ACB')
D. (BDA')
Câu 3. Số đường tiệm cận của đồ thị hàm số y=x−22x+1 là
A. 0.
B. 3.
C. 1.
D. 2.
Câu 4. Số cạnh của hình bát diện đều là :
A. 10.
B. 6.
C. 8
D. 12.
Câu 5. Giá trị nhỏ nhất của hàm số y=x+4x trên khoảng (0;+∞) bằng
A.3.
B.4.
C. 5.
D. 1.
Câu 6. Giá trị lớn nhất của hàm số y=x3−3x+2 trên đoạn [-3;3] bằng
A. 20.
B. 4.
C. 0.
D. - 16.
Câu 7. Tính giá trị biểu thức P=9log24−8log23.
A. P = - 11.
B. P = - 17.
C. P = 0.
D. P = - 1.
Câu 8. Tính thể tích khối lăng trụ tam giác đều có tất cả các cạnh bằng a.
A. √3a36.
B. √3a34.
C. √3a312.
D. √2a34.
Câu 9. Cho khối chóp có diện tích đáy bằng B, chiều cao bằng h. Thể tích V của khối chóp đó là
A. V=Bh
B. V=3Bh
C. V=13B.h.
D. V = B.h.
Câu 10. Hàm số y=x3−3x nghịch biến trên khoảng nào sau đây?
A. (0;+∞).
B. (1;+∞).
C. (−1;1).
D. (−∞;3).
Câu 11. Hình vẽ bên là đồ thị của hàm số nào dưới đây ?
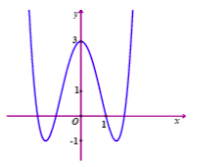
A. y=−x4−2x2+3.
B. y=x4−4x2+3.
C. y=x4−2x2−3.
D. y=x3−4x2+3.
Câu 12. Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau :

Hàm số y = f(x) nghịch biến trên khoảng nào trong các khoảng sau đây ?
A. (−2;+∞).
B. (-2;1).
C. (−∞;−2).
D. (1;3).
II. TỰ LUẬN (7 điểm)
Câu 13 (1,0 điểm). Gọi A, B là các điểm cực trị của đồ thị hàm số y=x3+3x2−4. Tính độ dài đoạn thẳng AB.
Câu 14 (1,0 điểm). Rút gọn biểu thức:
P=a√3+1.a2−√3(a√2−2)√2+2, với a > 0.
Câu 15 (1,0 điểm). Viết phương trình tiếp tuyến của đồ thị hàm số (C):y=2x−3x+1 tại giao điểm của (C) với trục tung.
Câu 16 (1,0 điểm). Tìm tất cả các giá trị của tham số m để đường thẳng d: y = 7x + m cắt đồ thị hàm số (C):y=x3+2x2−2 tại 3 điểm phân biệt.
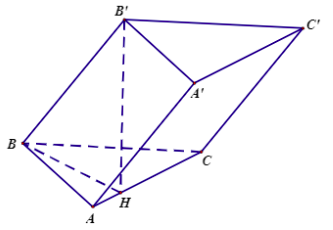
Câu 17 (1,0 điểm). Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại B. Gọi H là chân đường cao kẻ từ B xuống AC, biết B′H⊥(ABC) và AB=1,AC=2,AA′=√5. Tính thể tích của khối lăng trụ đã cho.
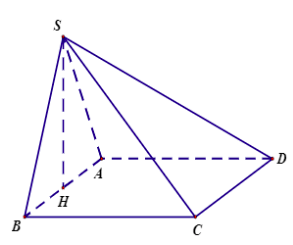
Câu 18 (0,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD theo a.
Câu 19 (0,5 điểm). Cho các số thực a, b thỏa mãn a > b > 1. Tìm giá trị nhỏ nhất của biểu thức P=log2ab(ab)+12logb(ab)−2.
HƯỚNG DẪN CHẤM
PHẦN I: TRẮC NGHIỆM (3 điểm)
1D 2A 3D 4D 5B 6A 7A 8B 9C 10C 11B 12C
PHẦN II: TỰ LUẬN (7 điểm)
|
Câu |
Đáp án |
Điểm |
|
13
|
Có y′=3x2+6x,y′=0 ⇔[x=0⇒y=−4x=−2⇒y=0 Đồ thị hàm số có hai điểm cực trị là A(0;−4),B(−2;0). Độ dài AB=√(−2)2+42=2√5. |
1,0 điểm |
|
14
|
P=a√3+1.a2−√3(a√2−2)√2+2=a√3+1+2−√3a(√2−2)(√2+2) P=a3a2−4=a5. |
1,0 điểm |
|
15
|
Cho x=0⇒y=−3 nên (C) cắt Oy tại A(0;-3) Có y′=5(x+1)2⇒y′(0)=5. Phương trình tiếp tuyến của (C) tại A là y = 5x - 3. |
1,0 điểm |
|
16 |
Xét phương trình hoành độ giao điểm x3+2x2−2=7x+m⇔x3+2x2−7x−2=m Xét hàm số f(x)=x3+2x2−7x−2, có f′(x)=3x2+4x−7 f′(x)=0⇔[x=1x=−73 BBT
Từ BBT suy ra để phương trình đã cho có ba nghiệm phân biệt thì −6<m<33827. |
1,0 điểm |
|
17 |
Ta có AB=1,AC=2 ⇒BC=√AC2−AB2=√3. Vậy SABC=12BA.BC=√32 BH=BA.BCAC=1.√32=√32. B′H=√BB′2−BH2=√5−34=√172. Do đó VABC.A′B′C′=B′H.SABC=√172⋅√32=√514. |
1,0 điểm |
|
18 |
Gọi H là trung điểm AB ⇒SH⊥(ABCD). Do SAB đều cạnh a nên SH=a√32. Diện tích đáy SABCD=a2 Thể tích khối chóp cần tìm là V=13SH.SABCD=13⋅a√32⋅a2=√3a36. |
0,5 điểm |
|
19 |
Có P=log2ab(ab)+12logb(ab)−2 =[logab(ab⋅b2)]2+12logb(ab)−2 =(1+2logabb)2+12logabb−2 Đặt t=logabb,t>0 do a > b > 1 Khi đó, P=f(t)=(1+2t)2+12t−2=4t2+4t+12t−1 với t > 0 Có f′(t)=8t+4−12t2=8t3+4t2−12t2, f′(t)=0⇔t=1. BBT
Từ BBT suy ra giá trị nhỏ nhất của P là minP=min(0;+∞)f(t)=19. Dấu “=” xảy ra khi t=1⇔logabb=1⇔b=ab⇔a=b2 |
0,5 điểm |
2. Đề thi học kì 1 môn Toán 12 số 2
TRƯỜNG THPT HOÀNG HOA THÁM
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 10
Thời gian: 90 phút (không kể thời gian giao đề)
Câu 1: Một khối nón có đường sinh bằng 2a và diện tích xung quanh của mặt nón bằng πa2. Tính thể tích của khối nón đã cho?
A. V=πa3√724
B. V=πa3√1512
C. V=πa3√1524
D. V=πa3√158
Câu 2: Đồ thị hàm số y=2x+1x−1 là (C). Phương trình tiếp tuyến của (C) biết tiếp tuyến đó song song với đường thẳng d: y=-3x+15 là:
A. y= -3x +10, y= -3x -5
B. y= -3x-1, y=-3x+11
C. y= -3x+1
D. y= -3x-11
Câu 3: Một hình chóp tam giác có đường cao bằng 100cm và đáy là tam giác vuông có độ dài hai cạnh góc vuông lần lượt bằng 20cm và 21cm. Thể tích của khối chóp đó bằng
A. 7000√2cm3
B. 6000cm3
C. 7000cm3
D. 6213cm3
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC. Thể tích của khối cầu ngoại tiếp hình chóp AHKCB là:
A. √2πa33.
B. πa36.
C. √2πa3
D. πa32.
Câu 5: Bà A gửi 100 triệu đồng vào ngân hàng theo thể thức lãi kép (đến kỳ hạn mà người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kỳ kế tiếp) với lãi suất 7% /năm. Hỏi sau 2 năm bà thu được lãi là bao nhiêu? (Giả sử lãi suất không thay đổi).
A. 20 (triệu đồng)
B. 14,50 (triệu đồng)
C. 14,49 (triệu đồng)
D. 15 (triệu đồng)
Câu 6: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD với BC=2AB,SA⊥(ABCD) và M là điểm trên cạnh AD sao cho AM = AB; Gọi V1,V2 lần lượt là thể tích của hai khối chóp S.ABM và S.ABC thì V1V2 bằng
A. 18
B. 12
C. 14
D. 16
Câu 7: Hàm số y=xπ+1+(x2−1)2e có tập xác định là:
A. R \ {-1; 1}
B. (1;+∞)
C. (-1;1)
D. R
Câu 8: Cho 0 < a < 1. Câu nào sai trong các câu sau?
A. Nếu x1<x2 thì ax1<ax2
B. ax>1 khi x < 0
C. 0<ax<1 khi x > 0
D. Trục hoành là tiệm cận ngang của đồ thị hàm số y=ax
Câu 9: Hàm số nào dưới đây không có cực trị?
A. y=−x3+5x2−2
B. y=x3+x−2
C. y=x−cosx
D. y=x4−3x2−2
Câu 10: Giải phương trình log2(x2+2x−3)=log2(6x+2) được
A. x = -1
B. x = 5
C. [x=−1x=5
D. [x=1x=−5
---Để xem tiếp nội dung và đáp án của Đề thi số 2, các em vui lòng chọn chức năng Xem Online hoặc tải về máy tính---
3. Đề thi học kì 1 môn Toán 12 số 3
TRƯỜNG THPT TRƯNG VƯƠNG
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 10
Thời gian: 90 phút (không kể thời gian giao đề)
Câu 1. Đường tiệm cận đứng của đồ thị hàm số y=2−xx+2 có phương trình là
A. x = -2
B. y = 2
C. y = -1
D. x = -1
Câu 2. Tìm tập xác định D của hàm số y=x+2x−1.
A. D=(−∞;−2)∪(1;+∞).
B. D=(−∞;1).
C. D=(1;+∞).
D. D=R∖{1}.
Câu 3. Tìm giá trị cực tiểu yCT của hàm số y=x3−3x2−9x+2
A. yCT=−25.
B. yCT=−24.
C. yCT=7.
D. yCT=−30.
Câu 4. Cho hàm số y=x+1x−1. Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số đồng biến trên khoảng (−∞;1) và nghịch biến trên khoảng (1;+∞).
B. Hàm số nghịch biến trên R \ {1}.
C. Hàm số nghịch biến trên các khoảng (−∞;1) và (1;+∞).
D. Hàm số nghịch biến trên R.
Câu 5. Cho hàm số y=−x3+3x2−3x+1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn luôn nghịch biến.
B. Hàm số luôn luôn đồng biến.
C. Hàm số đạt cực đại tại x = 1
D. Hàm số đạt cực tiểu tại x = 1
Câu 6. Hàm số y=x3+3x2−4 nghịch biến khi x thuộc khoảng nào sau đây:
A. (-3;0)
B. (-2;0)
C. (−∞;−2)
D. (0;+∞)
Câu 7. Tìm giá trị lớn nhất của hàm số f(x)=x3−3x+2 trên đoạn [-1;2].
A. max[−1;2]f(x)=−2.
B. max[−1;2]f(x)=0.
C. max[−1;2]f(x)=4.
D. max[−1;2]f(x)=2.
Câu 8. Đồ thị ở hình bên là của hàm số nào?
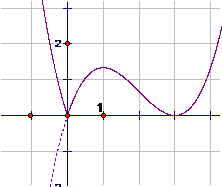
A. y=|x3−2x2+3x|
B. y=|x|3−2x2+3|x|
C. y=|13x3−2x2+3x|
D. y=13|x|3−2x2+3|x|
Câu 9. Cho hàm số y = f(x) xác định trên R∖{±1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ. Số đường tiệm cận của đồ thị hàm số là
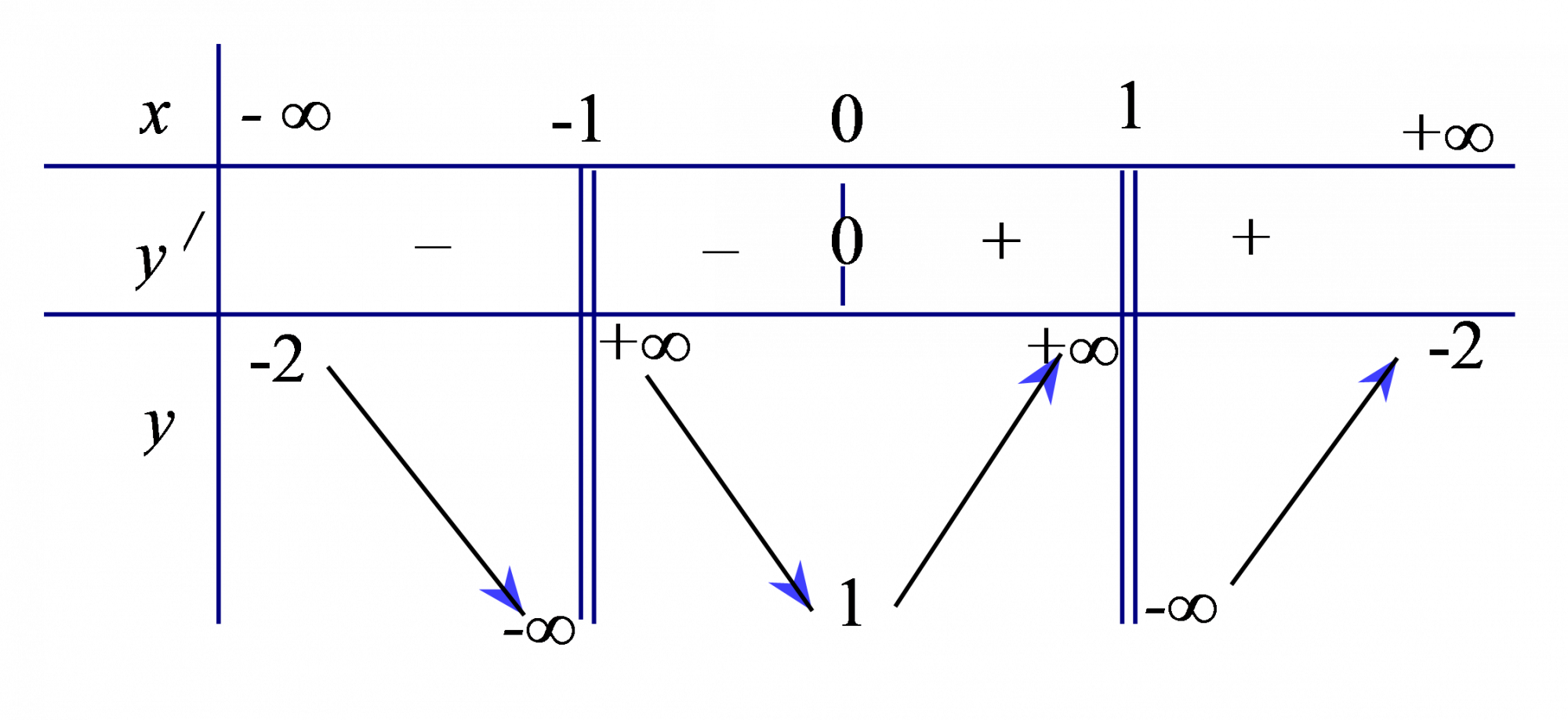
A. 1
B. 2
C. 3
D. 4
Câu 10. Số giao điểm của ĐTHS y=2x4−x2 với trục hoành là:
A. 0
B. 1
C. 2
D. 3
---Để xem tiếp nội dung và đáp án của Đề thi số 3, các em vui lòng chọn chức năng Xem Online hoặc tải về máy tính---
4. Đề thi học kì 1 môn Toán 12 số 4
TRƯỜNG THPT NGUYỄN DU
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 10
Thời gian: 90 phút (không kể thời gian giao đề)
Câu 1: Cho hàm số y=log2x2. Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên (0;+∞)
B. Hàm số nghịch biến trên (−∞;0)
C. Đồ thị hàm số có một tiệm cận ngang.
D. Đồ thị hàm số có một đường tiệm cận đứng.
Câu 2: Khoảng đồng biến của hàm số y=√2x−x2 là:
A. (1;2)
B. (−∞;1)
C. (1;+∞)
D. (0;1)
Câu 3: Thể tích của khối cầu có bán kính 6cm là
A. 216π(cm3)
B. 288π(cm3)
C. 432π(cm3)
D. 864π(cm3)
Câu 4: Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên
.png)
Khẳng định nào sau đây đúng ?
A. Phương trình f(x) = 0 có 2 nghiệm.
B. Hàm số có đúng một cực trị
C. Hàm số có giá trị nhỏ nhất bằng -3
D. Hàm số có giá trị lớn nhất bằng 1
Câu 5: Hàm số y=(x3−3x+3)ex có đạo hàm là:
A. (2x−3)ex
B. −3xex
C. (x2−x)ex
D. x2ex
---Còn tiếp---
5. Đề thi học kì 1 môn Toán 12 số 5
TRƯỜNG THPT HÀN THUYÊN
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 10
Thời gian: 90 phút (không kể thời gian giao đề)
Câu 1: Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên
.png)
Hàm số đồng biến trên khoảng nào sau đây?
A. (−27;+∞)
B. (−∞;5)
C. (−∞;−1)
D. (−1;+∞)
Câu 2: Tập nghiệm S của bất phương trình 32x−3≥9 là
A. S=[52;+∞)
B. S=(−∞;52]
C. S=(−∞;12]
D. S=[12;+∞)
Câu 3: Cho khối chóp có đáy là hình vuông cạnh 2a và chiều cao bằng 3a. Thể tích của khối chóp đã cho bằng
A. 4a3
B. 12a3
C. a3
D. 3a3
Câu 4: Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Diện tích toàn phần Stp của hình nón là:
A. Stp=πRl+2πR2
B. Stp=2πRl+2πR2
C. Stp=2πRl+πR2
D. πRl+πR2
Câu 5: Hàm số y=(2x−4)23 có tập xác định là
A. R
B. R \ {2}
C. (−2;+∞)
D. (2;+∞)
---Còn tiếp---
6. Đề thi học kì 1 môn Toán 12 số 6
TRƯỜNG THCS - THPT HAI BÀ TRƯNG
ĐỀ THI HK1
NĂM HỌC: 2020-2021
MÔN: TOÁN – LỚP 10
Thời gian: 50 phút (không kể thời gian giao đề)
Câu 1. Hàm số y=2x2+1 nghịch biến trên khoảng nào dưới đây ?
A. (− ∞; + ∞)
B. (− 1; 1) .
C. (0; + ∞).
D. (− ∞; 0) .
Câu 2. Hàm số y=x2−2xx−1 đồng biến trên khoảng:
A. (0;+∞)
B. (−∞;2)
C. (−∞;1) và (1;+∞)
D. (−1;+∞)
Câu 3. Hàm số y=√2x−x2 nghịch biến trên khoảng:
A. (1;2)
B. (1;+∞)
C. (0;1)
D. (0;2)
Câu 4. Hàm số y=x−m2x−4 đồng biến trên các khoảng (−∞;4) và (4;+∞) khi:
A. [m<−2m>2
B. [m≤−2m≥2
C. −2≤m≤2
D. −2<m<2
Câu 5. Số tiệm cân đứng của đồ thị hàm số y=√x+25−5x2+x là:
A. 2
B. 0
C. 1
D. 3
---Còn tiếp---
7. Đề thi học kì 1 môn Toán 12 số 7
Trường THPT Lê Quý Đôn
Số câu: 50 câu trắc nghiệm
Thời gian: 90 phút (không kể thời gian giao đề)
Năm học: 2020-2021
8. Đề thi học kì 1 môn Toán 12 số 8
Trường THPT Lương Thế Vinh
Số câu: 50 câu trắc nghiệm
Thời gian: 90 phút (không kể thời gian giao đề)
Năm học: 2020-2021
9. Đề thi học kì 1 môn Toán 12 số 9
Trường THPT Lý Thánh Tông
Số câu: 50 câu trắc nghiệm
Thời gian: 90 phút (không kể thời gian giao đề)
Năm học: 2020-2021
10. Đề thi học kì 1 môn Toán 12 số 10
Trường THPT Trần Phú
Số câu: 50 câu trắc nghiệm
Thời gian: 90 phút (không kể thời gian giao đề)
Năm học: 2020-2021
-Bấm TẢI VỀ hoặc chọn chức năng XEM ONLINE để xem đầy đủ nội dung các Đề thi 1-10-
Tham khảo thêm
- docx 10 Đề kiểm tra HK1 môn Toán 12 năm 2019 có đáp án



.png)

