10 đề thi giữa HK1 môn Toán học 12 năm 2020 có đáp án

ĐỀ THI GIỮA HKI

TRƯỜNG THPT YÊN PHONG 2

NĂM HỌC: 2020 - 2021

MÔN: TOÁN

Thời gian làm bài: 45 phút

Câu 1. Hàm số \(y=x^{2}-\frac{1}{2} x^{4}\) nghịch biến trên khoảng nào sau đây?

A. \((-\infty ;-1)\)

B. \((1 ;+\infty)\)

C. \((0 ;+\infty)\)

D. (-1 ; 1)

Câu 2. Có bao nhiêu mặt phẳng cách đều tất cả các đỉnh của một hình lăng trụ tam giác ?

A. 4.

B. 1 .

C. Vô số.

D. 3

Câu 3. Tìm giá trị lớn nhất của hàm số \(y=\sqrt{1-2 x}\) trên đoạn [-4 ; 0]

A. 1.

B. 4 .

C. 3.

D. 0.

Câu 4. Phép tịnh tiến theo \(\vec{v}=(2 ;-1)\) biến điểm M(5 ; 0) thành điểm M'. Tìm tọa độ điểm M'.

A. M'(-1 ; 2)

B. M'( 7 ;-1)

C. M'( 5 ;-1)

D. M'(-3 ;-1)

Câu 5. Hàm số nào sau đây là hàm đa thức bậc ba ?

A. \(y=x^{2}+x^{3}-x\)

B. \(y = - {x^2} + x + 3\)

C. \(y=x^{3}+x^{2}-x^{4}\)

D. y = 2x + 1

Câu 6. Cho hàm số \(y=\frac{5 x-1}{x+2} .\) Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên mỗi khoảng \((-\infty ;-2),(-2 ;+\infty)\).

B. Hàm số đồng biến trên tập xác định.

C. Hàm số đồng biến trên \(\mathbb{R} \backslash\{-2\}\).

D. Hàm số đồng biến trên \((-\infty ;-2) \cup(-2 ;+\infty)\).

Câu 7. Cho hình lăng trụ ABC.A'B'C'.  Xét vị trí tương đối của hai đường thẳng AB, B'C'.

A. Trùng nhau.

B. Song song.

C. Cắt nhau.

D. Chéo nhau.

Câu 8. Một hình tứ diện có bao nhiêu đỉnh?

A. 7 .

B. 5 .

C. 4 .

D. 6 .

Câu 9. Gọi giá trị lớn nhất và nhỏ nhất của hàm số \(y=-x^{3}-x^{2}\) trên đoạn [-1 ; 2] là M, m . Tính M.m.

A. -12

B. 0

C. 1

D. -1 .

Câu 10. Điểm nào sau đây thuộc đồ thị hàm số y = 2x - 1?

A. M(1 ; 1)

B. Q(-1 ; 1)

C. N(1 ;-1)

D. P(-1 ;-1)

Câu 11. Viết phương trình tiếp tuyến của đồ hàm số \(y=-x^{3}+x^{2}-1\) tại điểm có tung độ bằng 1 .

A. y = -x

B. y = -x + 1

C. y = -5 x - 4

D. y = -5 x + 6

Câu 12. Phương trình nào sau đây vô nghiệm?

A. tan x = 12

B. \(\cos x=\sqrt{5}\)

C. \(\cot x=-\sqrt{2}\)

D. \(\sin x=-0,5\)

Câu 13. Tìm tập xác định của hàm số \(y=\frac{2021}{x}\).

A. \(\mathbb{R} \backslash\{0\}\).

B. \(\mathbb{R}\).

C. \((0 ;+\infty)\).

D. \(\mathbb{R} \backslash\{2021\}\)

Câu 14. Hàm số nào sau đây có tập xác định là \(\mathbb{R}\)?

A. \(y=x^{2}-x^{4}\)

B. y = tanx

C. \(y=\frac{1+x}{2 x-1}\)

D. \(y=\sqrt{x}\)

Câu 15. Một hình chóp có 2021 mặt thì có bao nhiêu cạnh?

A. 4042 .

B. 4040 .

C. 2022 .

D. 2020 .

Câu 16. Đường thẳng có phương trình nào sau đây là tiệm cận ngang của đồ thị hàm số \( y=\frac{2-3 x}{x+1}\)?

A. x = -1

B. y = 2

C. x = -3

D. y = -3

Câu 17. Tính giới hạn \(\lim \frac{3 n-1}{n+14}\).

A. 0 .

B. 3 .

C. \(\frac{1}{3}\).

D. \(+\infty\).

Câu 18. Tìm tung độ giao điểm của đồ thị hàm số \(y=\frac{2 x-1}{x+3}\) với trục tung.

A. -3.

B. \(\frac{1}{2}\)

C. \(-\frac{1}{3}\)

D. 0 

Câu 19. Tìm giá trị nhỏ nhất của hàm số \(y=x^{4}-2 x^{2}-1\) trên đoạn [0 ; 3].

A. 0 

B. -2 

C. -1 

D. 1 

Câu 20. Trong không gian, khẳng định nào sau đây đúng?

A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phằng thì song song với nhau.

B. Hai mặt phằng phân biệt cùng vuông góc với mặt phằng thứ ba thì song song với nhau.

C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thằng thì vuông góc với nhau.

D. Hai đường thẵng phân biệt cùng vuông góc với đường thằng thứ ba thì song song với nhau.

Câu 21. Cho hình chóp S.ABC có SA = 1, SB = 2, SC = 3 và đôi một vuông góc. Tính khoảng cách từ điểm S đến mặt phằng (ABC).

A. \(\frac{6}{11}\)

B. \(\frac{1}{\sqrt{6}}\)

C. \(\frac{6}{7}\)

D. \(\sqrt{6}\)

Câu 22. Viết phương trình tiếp tuyến của đồ hàm số \(y=-3 x^{2}+1\) biết rằng tiếp tuyến song song với đường thẳng \(12 x+2 y-8=0\)

A. y= -6x - 2

B. Không có tiếp tuyến.

C. y = -6x + 4

D. y = -6x - 8

Câu 23. Cho hình chóp S.ABC có các tam giác SAB, SAC, SBC vuông cân tại đỉnh S. Gọi M là trung điểm của cạnh AB. Tính góc giữa hai vectơ \(\overrightarrow{S M}, \overrightarrow{B C}\)

A. 120^o

B. 30^o

C. 60^o

D. 45^o

Câu 24. Có bao nhiêu giá trị của tham số m để đồ thị hàm số \(y=\frac{2 x-1}{m x+2}$\)không có tiệm cận?

A. 0

B. 3 

C. 2 

D. 1

Câu 25. Cho hình hộp chữ nhật ABCD.A'B'C'D' có ABCD là hình vuông cạnh a và \(AA^{\prime}=a \sqrt{2}\). Tính góc giữa đường thằng AC' và mặt phằng ABCD.

A. 45^o

B. 75^o

C. 30^o

D. 60^o

Câu 26. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\left(m-m^{2}\right) x^{4}+\left(m^{2}+m\right) x^{2}+2020\) có một điểm cực trị?

A. 2 .

B. 3 .

C. 4 .

D. 1 .

Câu 27. Cho hình chóp cụt đều, có hai đáy là các hình lục giác đều cạnh bằng 2 và cạnh bằng 4. Chiều cao của hình chóp cụt bằng 2. Tính diện tích toàn phần của hình chóp cụt đó.

A. \(18 \sqrt{7}+12 \sqrt{3}\)

B. \(18 \sqrt{7}+30 \sqrt{3}\)

C. \(8 \sqrt{3}+3 \sqrt{2}\)

D. \(24 \sqrt{3}+9 \sqrt{2}\)

Câu 28. Có bao nhiêu giá trị nguyên nhỏ hơn 2021 của tham số m để hàm số \(y=\left|x^{3}+x^{2}-m x-1\right|\) có 5 điểm cực trị?

A. Vô số.

B. 2019.

C. 2020 .

D. 2021.

Câu 29. Tìm m để hàm số \(y=\frac{x-1}{2 x+m}\) nghịch biến trên khoảng \((3 ;+\infty)\).

A. \(-6 \leq m<-2\)

B. \(-2<m \leq 6\)

C. \(m \leq 3\)

D. \(m<-2\)

Câu 30. Hàm số \(y=\frac{2 x+4}{x-1}\) có đồ thị (C). Tiếp tuyến bất kì của (C) cắt hai đường tiệm cận của nó tại A, B. Tìm giá trị nhỏ nhất của bán kính đường tròn ngoại tiếp tam giác IAB, ở đó I là giao điểm của hai

đường tiệm cận của (C).

A. 24 .

B. \(2 \sqrt{3}\).

C. \(4 \sqrt{3}\).

D. 12 .

---HẾT---

ĐÁP ÁN

ĐỀ THI GIỮA HKI

TRƯỜNG THPT THUẬN THÀNH 1

NĂM HỌC: 2020 - 2021

MÔN: TOÁN

Thời gian làm bài: 45 phút

Câu 1: Giá trị của \(\lim _{x \rightarrow 1}\left(3 x^{2}-2 x+1\right)\) bằng:

A. 2 

B. 3

C. \(+\infty\)

D. 1

Câu 2: Tìm số hạng không chứa x trong khai triển của \(\left(x \sqrt{x}+\frac{1}{x^{4}}\right)^{n},\) với x > 0, nếu biết rằng \(C_{n}^{2}-C_{n}^{1}=44\)

A. 525

B. 485

C. 165

D. 238

Câu 3: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED = 3E C. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là.

A. Tam giác MNE.

B. Tứ giác MNEF với F là điểm bất kì trên cạnh BD.

C. Hình bình hành MNEF với F là điểm trên cạnh BD mà EF // BC.

D. Hình thang MNEF với F là điểm trên cạnh BD mà EF // BC.

Câu 4: Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau lập từ các chữ số 1, 2, 3, 4, 5?

A. 900 

B. 60 

C. 125 

D. 20 

Câu 5: Khi cắt hình chóp tứ giác S.ABCD bởi một mặt phằng, thiết diện không thể là hình nào?

A. Tứ giác.

B. Tam giác.

C. Lục giác.

D. Ngũ giác.

Câu 6: Tìm giá trị lớn nhất M của hàm số \(y=2 x^{3}+3 x^{2}-12 x+2\) trên đoạn [-1 ; 2].

A. M = 10.

B. M = 6.

C. M = 11.

D. M=15.

Câu 7: Cho hình lăng trụ đều BAC.A'B'C' có cạnh đáy bằng 2a, cạnh bên bằng a. Tính góc giữa hai mặt phẳng \(\left(A B^{\prime} C^{\prime}\right)\) và \(\left(A^{\prime} B^{\prime} C^{\prime}\right)\).

A. \(\arccos \frac{\sqrt{3}}{4}\)

B. \(\arcsin \frac{\sqrt{3}}{4}\)

C. \(\frac{\pi}{3}\).

D. \(\frac{\pi}{6}\).

Câu 8: Cho cấp số cộng có tổng n số hạng đầu là \(S_{n}=4 n^{2}+3 n, n \in \mathbb{N}^{*}\) thì số hạng thứ 10 của cấp số cộng là

A. \(u_{10}=79\)

B. \(u_{10}=71\)

C. \(u_{10}=95\)

D. \(u_{10}=87\)

Câu 9: Giá trị giới hạn \(\lim _{x \rightarrow-\infty} \frac{\sqrt{x^{2}-x}-\sqrt{4 x^{2}+1}}{2 x+3}\) bằng:

A. \(-\infty\).

B. \(-\frac{1}{2}\)

C. \(\frac{1}{2}\).

D. \(+\infty\).

Câu 10: Cho ba số a, b, c theo thứ tự đó vừa lập thành cấp số cộng, vừa lập thành cấp số nhân khi và chỉ khi

A. \(a=q ; b=q^{2} ; c=q^{3}\) với \(q \neq 0\) cho trước.

B. \(a=1 ; b=2 ; c=3\).

C. \(a=d ; b=2 d ; c=3 d\) với \(d \neq 0\) cho trước.

D. \(a=b=c\).

---Để xem tiếp nội dung và đáp án của Đề thi số 2, các em vui lòng chọn chức năng Xem Online hoặc tải về máy tính---

ĐỀ THI GIỮA HKI

TRƯỜNG THPT NGUYỄN THỊ MINH KHAI

NĂM HỌC: 2020 - 2021

MÔN: TOÁN

Thời gian làm bài: 45 phút

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a và SA vuông góc với đáy. Góc giữa SC và đáy bằng 45^o. Tính theo a thể tích khối chóp S.ABCD

A. \(8 \sqrt{2} a^{3}\)

B. \(\frac{8 \sqrt{2} a^{3}}{3}\)

C. \(16 \sqrt{2} a^{3}\)

D. \(\frac{4 \sqrt{3} a^{3}}{3}\)

Câu 2: Giá trị lớn nhất của hàm số \(y=\frac{x+1}{x-2}\) trên đoạn [-1 ; 0] là

A. \(-\frac{2}{3}\)

B. 0

C. \(-\frac{1}{2}\)

D. 2

Câu 3: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=-x^{4}+8 x^{2}-2\) trên đoạn [-3 ; 1]. Tính M + m?

A. -25

B. 3

C. -6

D. -48

Câu 4: Kết luận nào sau đây vè tính đơn điệu của hàm số \(y=\frac{2 x+1}{x+1}\) là đúng?

A. Hàm số nghịch biến trên các khoảng \((-\infty ;-1) \ và \ (-1 ;+\infty) \). 

B. Hàm số đồng biến trên các khoảng \((-\infty ;-1) \ và \ (-1 ;+\infty) \)

C. Hàm số luôn luôn đồng biến trên \(\mathbb{R} \backslash\{-1\}\)

D. Hàm số luôn luôn nghịch biến trên \(\mathbb{R} \backslash\{-1\}\)

Câu 5: Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo đáy góc \(60^{\circ} .\) Thể tích của khối chóp đó bằng:

A. \(\frac{a^{3} \sqrt{3}}{12}\)

B. \(\frac{a^{3} \sqrt{3}}{6}\)

C. \(\frac{a^{3} \sqrt{3}}{36}\)

D. \(\frac{a^{3} \sqrt{3}}{18}\)

Câu 6: Số điểm cực trị của hàm số \(y=x^{4}-3 x^{2}+1\) là:

A. 3

B. 1

C. 2

D. 0

Câu 7: Hàm số \(y=\frac{1}{x^{2}+1}\) có bảng biến thiên như hình vẽ. Xét trên tập xác định của hàm số. Hãy chọn khẳng định đúng?

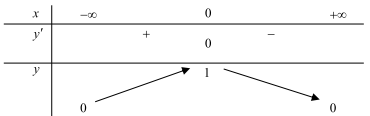
A. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số

B. Hàm số có giá trị lớn nhất bằng 1

C. Hàm số có giá trị lớn nhất bằng 0

D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0

Câu 8: Viết phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{x^{3}}{3}+3 x^{2}-2\) biết tiếp tuyến có hệ số góc \(k=-9\)

A. \(y-16=-9(x-3)\)

B. \(y+16=-9(x+3)\)

C. \(y-16=-9(x+3)\)

D. \(y=-9 x-27\)

Câu 9: Hàm số nào dưới đây có đồ thị như hình vẽ bên?

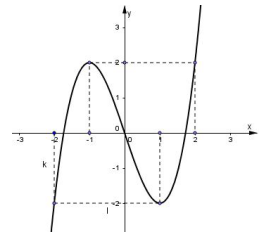
A. \(y=x^{3}-3 x\).

B. \(y=x^{4}-4 x^{2}\).

C. \(y=-x^{3}\).

D. \(y=x^{3}-3 x^{2}\).

Câu 10: Số giao điểm của đường cong \(y=x^{3}-2 x^{2}+x-1\) và đường thẳng \(y=1-2 x\) là:

A. 1

B. 2

3. 3

D. 0

---Để xem tiếp nội dung và đáp án của Đề thi số 3, các em vui lòng chọn chức năng Xem Online hoặc tải về máy tính---

ĐỀ THI GIỮA HKI

TRƯỜNG THPT NGUYỄN VĂN LINH

NĂM HỌC: 2020 - 2021

MÔN: TOÁN

Thời gian làm bài: 45 phút

Câu 1. Hàm số \(y=x^{3}-3 x^{2}+2\) nghịch biến trên khoảng nào?

A (0 ; 2)

B. \((2 ;+\infty)\)

C. (-2 ; 2)

D. \((0 ;+\infty)\)

Câu 2. Cho hàm số \(y=\frac{6 x+7}{6-2 x}\). Chọn khẳng định đúng.

A. Hàm số đồng biến trên mỗi khoảng \(\left(-\infty ; \frac{1}{3}\right)\) và khoảng \(\left(\frac{1}{3} ;+\infty\right)\).

B. Hàm số đồng biến trên mỗi khoảng \((-\infty ; 3)\) và khoảng \((3 ;+\infty)\).

C. Hàm số đồng biến trên khoảng \((-\infty ; 3) \cup(3 ;+\infty)\).

D. Hàm số nghịch biến trên mỗi khoảng \((-\infty ; 3)\) và khoảng \((3 ;+\infty)\).

Câu 3. Cho hàm số \(y=x^{3}+m x^{2}+3 x-2 m+5\) (với m là tham số thực). Hàm số đồng biến trên R khi

A. \(\left[\begin{array}{l}m \geq 3 \\ m \leq-3\end{array}\right.\) 

B. \(m \leq 3\)

C. \(-3 \leq m \leq 3\)

D. -3 < m < 3.

Câu 4. Các điểm cực tiểu của hàm số \( y=x^{4}+3 x^{2}+2\) là:

A. x = -1

B. x = 5 

C. x = 0 

D. x = 1, x = 2

Câu 5. Cho hàm số y = f(x) có đạo hàm \(f^{\prime}(x)=-2017(x-1)(x+2)^{3}(x-3)^{2}\). Tìm số điểm cục trị của f(x)

A. 3

B. 2

C. 0

C. 1

---Còn tiếp---

5. Đề thi giữa học kì 1 môn Toán 12 - Số 5

ĐỀ THI GIỮA HKI

TRƯỜNG THPT HAI BÀ TRƯNG

NĂM HỌC: 2020 - 2021

MÔN: TOÁN

Thời gian làm bài: 45 phút

Câu 1: Cho hàm số \(y = {x^3} + 3x + 2\). Mệnh đề nào dưới đây đúng ?

A. Hàm số đồng biến trên khoảng (−∞; 0) và nghịch biến trên khoảng (0; + ∞) .

B. Hàm số đồng biến trên khoảng (−∞;  + ∞) .

C. Hàm số nghịch biến trên khoảng (− ∞;  + ∞) .

D. Hàm số nghịch biến trên khoảng (− ∞; 0) và đồng biến trên khoảng (0; + ∞)

Câu 2: Tìm tất cả giá trị thực của m để hàm số \(y = \frac{1}{3}{x^3} - (m + 1){x^2} + {m^2}x - 1\) có 2 cực trị:

A. m > -1/2

B. \(m \le - 1/2\)

C. \(m \le 1/2\)

D. m > ½

Câu 3: Cho hàm số \(y = {x^4} - 2{x^2}\). Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên khoảng  (−∞;  − 2)

B. Hàm số đồng biến trên khoảng  (−∞;  − 2)

C. Hàm số đồng biến trên khoảng  (−1; 1) .             

D. Hàm số nghịch biến trên khoảng  (−1; 1) .

Câu 4: Tất cả giá trị của m để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + ({m^2} - m)x + 1\) có 1 cực đại và 1 cực tiểu là:

A. -1/2 < m <0

B. 0 < m < 1/2

C.  m > 0

D.  m < 0  

Câu 5: Hàm số \(f(x) = 2{x^4} + 1\) đồng biến trên khoảng nào?

A. \(( - \infty ; - \frac{1}{2})\).

B. \(( - \infty ;0)\)

C. \(( - \frac{1}{2}; + \infty )\) 

D. \((0; + \infty )\) 

---Còn tiếp---

6. Đề thi giữa học kì 1 môn Toán 12 - Số 6

ĐỀ THI GIỮA HKI

TRƯỜNG THPT PHAN BỘI CHÂU

NĂM HỌC: 2020 - 2021

MÔN: TOÁN

Thời gian làm bài: 45 phút

Câu 1:  Cho hàm số y = f(x) có đạo hàm trên R và có bảng xét dấu f'(x) như sau:

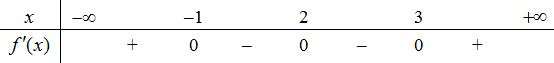
Mệnh đề nào sau đây đúng?

A. Hàm số y = f(x) nghịch biến trên khoảng \((3\,;\, + \infty ).\)

B. Hàm số y = f(x) nghịch biến trên khoảng (-1; 3).

C. Hàm số y = f(x) đồng biến trên khoảng (-1; 2)

D. Hàm số y = f(x) đồng biến trên khoảng \(( - \infty \,;\,2).\)

Câu 2: Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như sau:

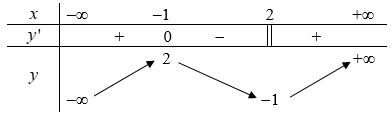
Mệnh đề nào sau đây đúng?

A. Hàm số y = f(x) có đúng một điểm cực trị.      

B. Hàm số y = f(x) đạt cực đại tại x = 2               

C. Hàm số y = f(x) đạt cực tiểu tại x = 2              

D. Hàm số y = f(x) đạt cực tiểu tại x = -1

Câu 3:  Đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 1}}{{2 - 3x}}\) là đường thẳng

A. \(x = - \frac{2}{3}.\)

B. \(y = - \frac{2}{3}.\)

C. \(x = \frac{1}{2}.\)

D. \(x = \frac{2}{3}.\)

Câu 4: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

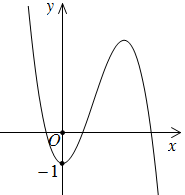
A. \(y = - {x^3} + 3{x^2} - 1\).

B. \(y = - {x^3} + 3{x^2} + 1\).

C. \(y = {x^4} - 3{x^2} - 1\).

D. \(y = {x^3} - 3{x^2} - 1\).

Câu 5: Với a là số thực dương tùy ý, \({a^3}.{a^{\frac{1}{2}}}\) bằng

A. \({a^{\frac{3}{2}}}.\)

B. \({a^{\frac{9}{2}}}.\)

C. \({a^{\frac{7}{2}}}.\)

D. \({a^{\frac{5}{2}}}.\)

---Còn tiếp---

Trường THPT Nguyễn Viết Xuân

Số câu: 30 câu trắc nghiệm

Thời gian làm bài: 45 phút

Năm học: 2020 - 2021

8. Đề thi giữa học kì 1 môn Toán 12 - Số 8

Trường THPT Nguyễn Đình Chiểu

Số câu: 30 câu trắc nghiệm

Thời gian làm bài: 45 phút

Năm học: 2020 - 2021

9. Đề thi giữa học kì 1 môn Toán 12 - Số 9

Trường THPT Thanh Đa

Số câu: 30 câu trắc nghiệm

Thời gian làm bài: 45 phút

Năm học: 2020 - 2021

10. Đề thi giữa học kì 1 môn Toán 12 - Số 10

Trường THPT Lê Quý Đôn

Số câu: 30 câu trắc nghiệm

Thời gian làm bài: 45 phút

Năm học: 2020 - 2021

-Bấm TẢI VỀ hoặc chọn chức năng XEM ONLINE để xem đầy đủ nội dung các Đề thi 1-10-