10 đề kiểm tra 15 phút Học kì 1 môn Toán 9 năm 2019 có đáp án

TRƯỜNG THCS NGÔ QUYỀN

ĐỀ KIỂM TRA 15 PHÚT

MÔN TOÁN 9

NĂM HỌC 2019-2020

Câu 1. Biểu thức \(\displaystyle \sqrt {1 - 2x} \) xác định khi 

A.\(\displaystyle x \ge \dfrac{1}{2}\)                         B. \(\displaystyle x \le \dfrac{1}{2}\)

C. \(\displaystyle x > \dfrac{1}{2}\)                           D. \(\displaystyle x < \dfrac{1}{2}\)

Câu 2. Điều kiện xác định của biểu thức \(\displaystyle \dfrac{{\sqrt x  + 1}}{{x - \sqrt x }}\) là

A.\(\displaystyle x \ne 0\)                        B. \(\displaystyle x > 0,x \ne 1\)

C. \(\displaystyle x \ge 0\)                       D. \(\displaystyle x \ge 0,x \ne 1\)

Câu 3. Biểu thức \(\displaystyle \sqrt {\dfrac{1}{{x - 1}}}  + \sqrt {2 - x} \) có nghĩa khi

A.\(\displaystyle x > 2\)                      B. \(\displaystyle x < 1\)

C. \(\displaystyle 1 < x \le 2\)             D. \(\displaystyle x \le 2,x \ne 1\)

Câu 4. Căn bậc hai số học của 64 là

A. 8 và -8                                               B. -8

C. 8                                                         D. 32.

Câu 5. Kết quả phép tính\(\displaystyle \sqrt {{{(\sqrt 3  - \sqrt 2 )}^2}} \)  là

A.\(\displaystyle \sqrt 3  - \sqrt 2 \)                     B. \(\displaystyle \sqrt 2  - \sqrt 3 \)

C. \(\displaystyle \pm (\sqrt 3  - \sqrt 2 )\)           D. 1

Câu 6. Kết quả của phép tính \(\displaystyle (2\sqrt 3  + \sqrt 2 )(2\sqrt 3  - \sqrt 2 )\) là

A.\(\displaystyle 4\sqrt 3 \)                        B. \(\displaystyle 2\sqrt 2 \)

C. 10                                              D. 14

Câu 7. Giá trị của biểu thức  \(\displaystyle {1 \over {2 + \sqrt 3 }} - {1 \over {2 - \sqrt 3 }}\) bằng

A.4                             B. 0

C. \(\displaystyle - 2\sqrt 3 \)                   D. \(\displaystyle 2\sqrt 3 \)

Câu 8. Giá trị của biểu thức \(\displaystyle \sqrt 3  - \sqrt {48}  + \sqrt {12} \) là

A.\(\displaystyle - \sqrt 3 \)                    B. \(\displaystyle \sqrt 3 \)

C. \(\displaystyle - 2\sqrt 3 \)                 D. \(\displaystyle 2\sqrt 3 \)

Câu 9. Giá trị của biểu thức \(\displaystyle \sqrt {{{(1 - \sqrt 2 )}^2}}  - \sqrt {{{(1 + \sqrt 2 )}^2}} \) là

A.0                                    B. -2

C.\(\displaystyle - \sqrt 2 \)                             D. \(\displaystyle - 2\sqrt 2 \)

Câu 10. Giá trị của biểu thức \(\displaystyle \)\(\displaystyle \left( {\sqrt {27}  - 3\sqrt {\dfrac{4}{3}}  + \sqrt {12} } \right):\sqrt 3 \) bằng

A.\(\displaystyle \sqrt 3 \)                         B. \(\displaystyle 2\sqrt 3 \)

C. \(\displaystyle - 2\sqrt 3 \)                  D.3

Câu 11. Giá trị của biểu thức \(\displaystyle \)\(\displaystyle \dfrac{{\sqrt 5 }}{{\sqrt {80} }}.\dfrac{{\sqrt {90} }}{{\sqrt {10} }}\) bằng

A.16                                                           B.0,75

C. 4                                                            D. 0,25.

Câu 12. Kết quả rút gọn của biểu thức \(\displaystyle \dfrac{{\sqrt {{x^2} - 6x + 9} }}{{x - 3}}\) với \(\displaystyle x > 3\) là

A.-1                                                            B. 1

C. \(\displaystyle \pm 1\)                                       D. kết quả khác.

Câu 13. Kết quả rút gọn của biểu thức \(\displaystyle {x^2}{y^2}.\sqrt {\dfrac{9}{{{x^2}{y^4}}}} \) với x

A. \(\displaystyle 3xy\)                                       B.\(\displaystyle {x^2}y\)

C. \(\displaystyle -3x\)                                       D. \(\displaystyle -3xy.\)

Câu 14. Tất cả các giá trị của x thỏa mãn \(\displaystyle \sqrt {4{x^2} + 4x + 1}  = 7\) là

A. \(\displaystyle x=3\)                                         B. \(\displaystyle x = \dfrac{{ - 7}}{2}\)

C. \(\displaystyle x=-3\)                                       D. \(\displaystyle x=-4;x=3.\)

ĐÁP ÁN ĐỀ KIỂM TRA 15 PHÚT SỐ 1 – MÔN TOÁN 9

TRƯỜNG THCS NGUYỄN HIỀN

ĐỀ KIỂM TRA 15 PHÚT

MÔN TOÁN 9

NĂM HỌC 2019-2020

Câu 1. Chứng minh rằng nếu \(a > 1\) thì \(a > \sqrt a .\) 

Câu 2. Chứng minh rằng với mọi x, ta có : \(\sqrt {{x^2} + 2x + 5}  \ge 2.\)

Câu 3. Chứng minh rằng \(\sqrt 3  - 5\) \(<-2\) (không dùng máy tính bỏ túi hay bảng số).

ĐÁP ÁN ĐỀ KIỂM TRA 15 PHÚT SỐ 2 – MÔN TOÁN 9

Câu 1: Ta có: \(a > 1 \Rightarrow \sqrt a  > \sqrt 1  \Leftrightarrow \sqrt a  > 1.\)

Nhân hai vế của bất đẳng thức trên với số dương \(\sqrt a \), ta được:

\(\sqrt a .\sqrt a  > \sqrt a  \Leftrightarrow a > \sqrt a .\)

Câu 2: Ta có: \({x^2} + 2x + 5 = {x^2} + 2x + 1 + 4 \) \(= {\left( {x + 1} \right)^2} + 4.\)

Vì \({\left( {x + 1} \right)^2} \ge 0,\) với mọi x thuộc \(\mathbb R\), nên :

\(\eqalign{  & {\left( {x + 1} \right)^2} + 4 \ge 4  \cr  &  \Rightarrow \sqrt {{{\left( {x + 1} \right)}^2} + 4}  \ge \sqrt 4   \cr  &  \Rightarrow \sqrt {{x^2} + 2x + 5}  \ge 2 \cr} \)

Câu 3: Ta có: \(\sqrt 3  -5< - 2 \Leftrightarrow \sqrt 3  < 5 - 2 \Rightarrow \sqrt 3  < 3\)

\( \Leftrightarrow {\left( {\sqrt 3 } \right)^2} < {3^2} \Leftrightarrow 3 < 9\) (hiển nhiên)

TRƯỜNG THCS NGUYỄN DU

ĐỀ KIỂM TRA 15 PHÚT

MÔN TOÁN 9

NĂM HỌC 2019-2020

Câu 1. Tìm điều kiện xác định của mỗi hàm số (Tìm tập xác định của hàm số) :

a) \(y = \sqrt { - x} \)

b) \(y = \sqrt {1 - x}  + \sqrt {1 + x} \) 

Câu 2. Cho hàm số \(y = f\left( x \right) = {x^2} + 1.\) Tính : \(f\left( 0 \right);\,f\left( { - 2} \right);\,f\left( {\sqrt 2 } \right)\)

Câu 3. Chứng minh hàm số \(y = f\left( x \right) = 2x\) đồng biến trên \(\mathbb R\).

ĐÁP ÁN ĐỀ KIỂM TRA 15 PHÚT SỐ 3 – MÔN TOÁN 9

Câu 1:

a) \(\sqrt { - x} \) xác định \( \Leftrightarrow  - x \ge 0 \Leftrightarrow x \le 0\)

b) \(\sqrt {1 - x}  + \sqrt {1 + x} \) xác định \( \Leftrightarrow \left\{ {\matrix{   {1 - x \ge 0}  \cr   {1 + x \ge 0}  \cr  } } \right. \Leftrightarrow \left\{ {\matrix{   {x \le 1}  \cr   {x \ge  - 1}  \cr  } } \right.\)

\(\Leftrightarrow  - 1 \le x \le 1\)

Câu 2: Ta có: 

\(\eqalign{  & f\left( 0 \right) = {0^2} + 1 = 1  \cr  & f\left( { - 2} \right) = {\left( { - 2} \right)^2} + 1 = 5  \cr  & f\left( {\sqrt 2 } \right) = {\left( {\sqrt 2 } \right)^2} + 1 = 3 \cr} \)

Câu 3: Với \({x_1},\,{x_2}\) bất kì thuộc \(\mathbb R\) và \({x_1}<{x_2}\). Ta có: \(f\left( {{x_1}} \right) = 2{x_1};f\left( {{x_2}} \right) = 2{x_2} \)

\(\Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = 2\left( {{x_1} - {x_2}} \right)\)

Vì \({x_1}<{x_2}\)

\(\eqalign{  &  \Rightarrow {x_1} - {x_2} < 0 \Rightarrow 2\left( {{x_1} - {x_2}} \right) < 0  \cr  &  \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) < 0 \cr&\Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right) \cr} \)

Vậy hàm số đã cho đồng biến trên \(\mathbb R\).

TRƯỜNG THCS QUANG TRUNG

ĐỀ KIỂM TRA 15 PHÚT

MÔN TOÁN 9

NĂM HỌC 2019-2020

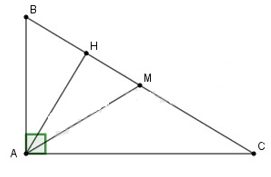
Cho ∆ABC vuông tại A, đường cao AH, biết \(AB = 15cm, BH = 9cm.\)

a. Tính AC, BC và đường cao AH 

b. Gọi M là trung điểm của BC. Tính diện tích tam giác AHM.

ĐÁP ÁN ĐỀ KIỂM TRA 15 PHÚT SỐ 4 – MÔN TOÁN 9

a) Ta có: ∆ABC vuông tại A, đường cao AH (gt)

\(A{B^2} = BC.BH\) (định lí 1)  

\( \Rightarrow BC = {{A{B^2}} \over {BH}}= {{{{15}^2}} \over 9} = 25\,\left( {cm} \right)\)

Theo định lí Pi-ta-go \(A{C^2} = B{C^2} - A{B^2}\)

\( \Rightarrow AC = \sqrt {B{C^2} - A{B^2}}  \)\(\;= \sqrt {{{25}^2} - {{15}^2}}  = 20\,\left( {cm} \right)\)

Lại có: AB.AC = BC.AH (định lí 3)

 \( \Rightarrow AH = {{AB.AC} \over {BC}} = {{15.20} \over {25}} = 12\,\left( {cm} \right)\)

b) M là trung điểm của BC (giả thiết)

\( \Rightarrow MB = MC = {{BC} \over 2} = {{25} \over 2} \)\(\:= 12,5\,\left( {cm} \right)  \)

\(\Rightarrow MH = MB - BH = 12,5 - 9\)\(\; = 3,5\,\left( {cm} \right) \)

Vậy \({S_{AHM}} = {1 \over 2}MH.AH = {1 \over 2}.3,5.12 \)\(\;= 21\,\left( {c{m^2}} \right)\)

5. Đề kiểm tra 15 phút môn Toán 9 – Số 5

TRƯỜNG THCS HƯƠNG KHÊ

ĐỀ KIỂM TRA 15 PHÚT

MÔN TOÁN 9

NĂM HỌC 2019-2020

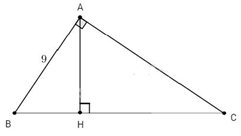
Cho \(∆ABC\) biết tỉ số giữa cạnh góc vuông và cạnh huyền là 4 : 5, cạnh góc vuông còn lại bằng 9cm. Tính độ dài hai hình chiếu của hai cạnh góc vuông lên cạnh huyền.

ĐÁP ÁN ĐỀ KIỂM TRA 15 PHÚT SỐ 5 – MÔN TOÁN 9

Giả sử tam giác ABC vuông tại A có chiều cao AH.

Đặt \(AB=c=9cm;AC=b;BC=a;AH=h;\)\(BH=c';CH=b'\)

Theo đề bài ta có \({b \over a} = {4 \over 5}\) và \(c = 9cm\) 

\(∆ABC\) vuông tại A, h là đường cao nên ta có: \(b.c = a.h\) (hệ thức lượng trong tam giác vuông)

\( \Rightarrow {h \over c} = {b \over a} = {4 \over 5}\)

\(hay\,\;{h \over 9} = {4 \over 5} \Rightarrow h = {{4.9} \over 5} = 7,2\,\left( {cm} \right)\)

Xét tam giác vuông \(AHB\), ta có: \(c{'^2} = {c^2} - {h^2}\) (định lí Pi-ta-go)

\( \Rightarrow c' = \sqrt {{9^2} - {{\left( {7,2} \right)}^2}}  = 5,4\)

Lại có: \({h^2} = b'.c'\)

\(\Rightarrow b' = {{{h^2}} \over {c'}} = {{7,{2^2}} \over {5,4}} = 9,6\left( {cm} \right)\)

6. Đề kiểm tra 15 phút môn Toán 9 – Số 6

TRƯỜNG THCS ĐỨC THỌ

ĐỀ KIỂM TRA 15 PHÚT

MÔN TOÁN 9

NĂM HỌC 2019-2020

Câu 1: Viết công thức nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của phương trình : \(2x + 0.y = 4.\)

Câu 2: Xác định một phương trình bậc nhất hai ẩn số, biết hai nghiệm là \(( 3; 5)\) và \(( 0; −2)\).

ĐÁP ÁN ĐỀ KIỂM TRA 15 PHÚT SỐ 6 – MÔN TOÁN 9

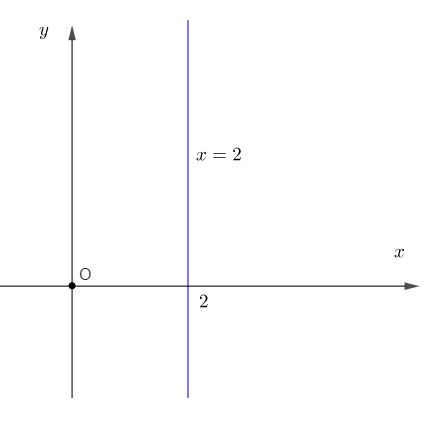
Câu 1: Ta có : \(x = 2.\)

Công thức  nghiệm tổng quát : \((2; y)\); y tùy ý.

Đường thẳng \(x = 2\) song song với Oy cắt Ox tại điểm có hoành độ bằng 2 ( xem hình vẽ).

Câu 2: Phương trình đường thẳng (d) : y = mx + n đi qua hai điểm \(( 3; 5)\) và \(( 0; −2)\) nên ta có:

Điểm \((0; −2)\) thuộc (d) \(=> n = −2.\) Khi đó : \(y = mx – 2.\)

Điểm \(( 3; 5)\) thuộc (d) => \(m = {7 \over 3}\)

Vậy : \(y = {7 \over 3}x - 2 \Leftrightarrow 7x - 3y - 6 = 0.\)

-----Còn tiếp-----

Trường THCS Lý Tự Trọng

Đề kiểm tra 15 phút

Môn: Toán 9

Năm học: 2019-2020

Số câu: 3 câu tự luận

8. Đề kiểm tra 15 phút môn Toán 9 – Số 8

Trường THCS Phan Đình Phùng

Đề kiểm tra 15 phút

Môn: Toán 9

Năm học: 2019-2020

Số câu: 3 câu tự luận

9. Đề kiểm tra 15 phút môn Toán 9 – Số 9

Trường THCS Nguyễn Đình Chiểu

Đề kiểm tra 15 phút

Môn: Toán 9

Năm học: 2019-2020

Số câu: 3 câu tự luận

10. Đề kiểm tra 15 phút môn Toán 9 – Số 10

Trường THCS Phan Đăng Lưu

Đề kiểm tra 15 phút

Môn: Toán 9

Năm học: 2019-2020

Số câu: 1 câu tự luận

---Bấm TẢI VỀ hoặc XEM ONLINE để xem đầy đủ nội dung các Đề thi 1-10---